S'évaluer

Limite de détection

Difficulté : ☆☆☆ Temps : 45 min

Un exercice précédent a montré que la vitesse réflexe de l'étoile dépend de la masse et de l'orbite de la planète via la relation :

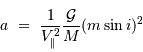
$a\ =\ {1\over V _{\mathrm{\parallel}}^{2}}{{\cal G}\over M}(m\sin i)^{2}$

Un graphe (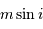 $m\sin i$ - rayon orbital 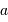) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 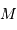de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.

Données numériques
objet	masse (kg)
Soleil	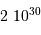$2\ 10^{30}$
Jupiter	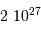$2\ 10^{27}$
la Terre	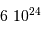$6\ 10^{24}$
1 UA	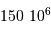$150\ 10^6$ km

Question 1)

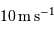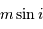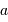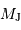Les mesures en 2000 atteignaient une précision en vitesse de l'ordre de $10 {\,\mathrm{m\,s}}^{-1}$ . En déduire la relation numérique entre les variables $m\sin i$ et correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et $M _{\mathrm{J}}$ .

Aide [3 points]

Question 2)

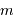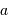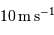Reporter la relation trouvée sur le diagramme masse-distance, avec comme unités la masse de Jupiter pour , et l'unité astronomique pour . Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de $10 {\,\mathrm{m\,s}}^{-1}$ ) ?

Aide [3 points]

Question 3)

Même question, si l'on parvient à détecter des amplitudes en vitesse de 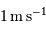$1 {\,\mathrm{m\,s}}^{-1}$ .

[1 points]

Question 4)

Montrer que Saturne, de période orbitale sidérale de l'ordre de 30 ans, ne pourrait tout de même pas être détecté avant l'année 2025.

Aide [1 points]

Question 5)

Montrer que cette technique d'observation comporte un biais, car elle favorise la détection de planète ayant des paramètres orbitaux particuliers.

[1 points]