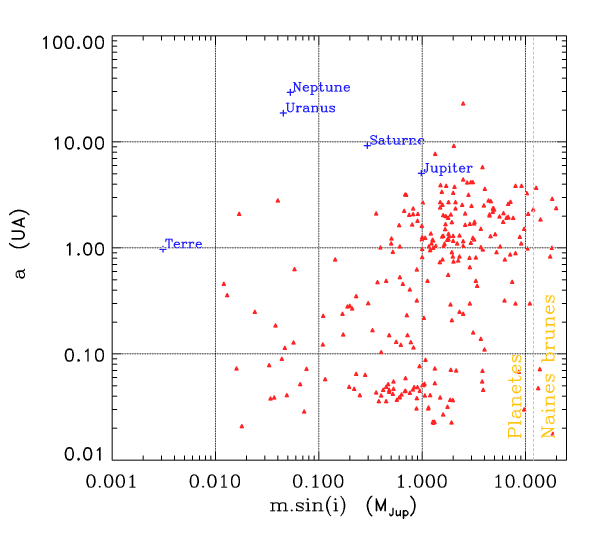
Systèmes pouvant être détectés par cette méthode
La méthode des vitesses radiales ne permet d'obtenir qu'une limite
inférieure de la masse des planètes, 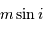 , car l'angle sous lequel
le système est observé,
, car l'angle sous lequel
le système est observé,  , reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse
, reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse 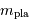 les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
- Plus la planète est massive, plus l'étoile est perturbée, car
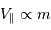 .
. - Plus la planète est proche, plus la période est courte et
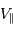 important, car
important, car 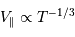 .
.
Il est commode de réécrire 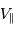 sous la forme :
sous la forme :
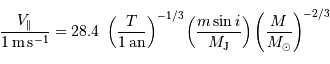
où 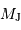 et
et 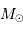 sont, respectivement, les masses de Jupiter et du Soleil.
sont, respectivement, les masses de Jupiter et du Soleil.
On rappelle, qu'avec les mêmes unités :
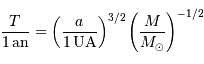
où 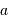 est exprimé en unité astronomique.
est exprimé en unité astronomique.
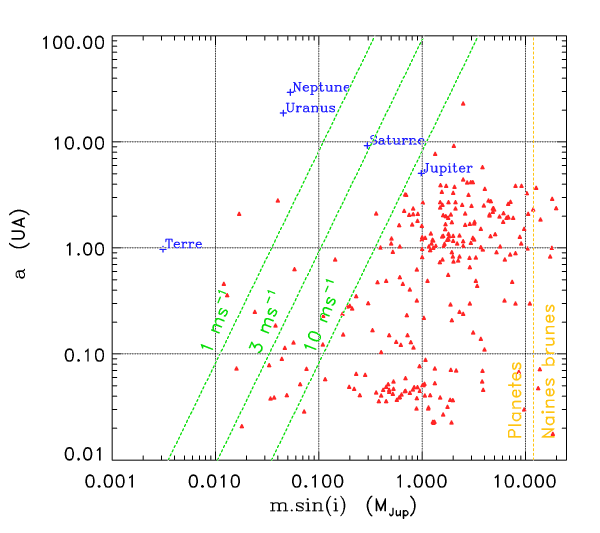
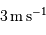 . Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des transits.
. Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des transits.
Limite de détection
La limite de détection des instruments utilisés actuellement est de l'ordre de 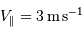 . Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse
. Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse 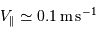 reste largement indétectable.
reste largement indétectable.
Néanmoins, il ne suffit pas que la vitesse réflexe de l'étoile soit supérieure à cette limite pour détecter une planète. En effet, une planète de masse égale à la masse de Jupiter va induire un effet Doppler de cet ordre pour une distance étoile-planète de 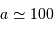 UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter
UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter 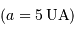 entraîne
entraîne 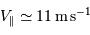 , ce qui est largement observable.
, ce qui est largement observable.
Les mesures de vitesses radiales pour la recherche de planètes extrasolaires sont menées systématiquement depuis 1995. Ceci limite la détection aux planètes de période orbitale inférieure à 15 ans en 2010, 30 ans en 2025...
Jusqu'à ce jour, la plupart des planètes extrasolaires détectées l'ont été par cette méthode. Un exercice traite de cette limite de détection.
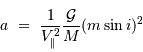
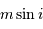 - rayon orbital
- rayon orbital 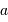 ) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse
) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 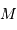 de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
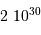
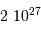
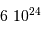
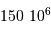 km
km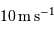 . En déduire la relation numérique entre les variables
. En déduire la relation numérique entre les variables 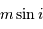 et
et 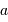 correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et
correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et 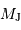 .
.
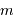 , et l'unité astronomique pour
, et l'unité astronomique pour 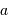 .
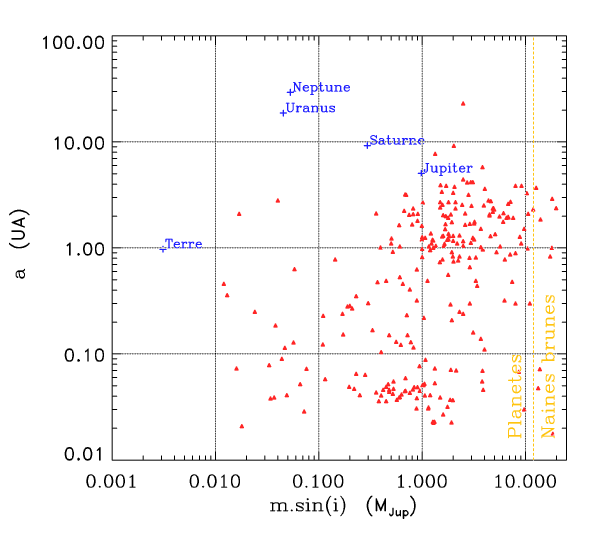
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de
.
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de 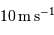 ) ?
) ?
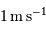 .
.