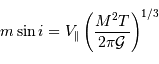|
Difficulté : ☆☆ Temps : 20 min
On s'intéresse à la distribution du facteur multiplicatif 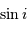 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 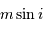 .
.
Montrer, en faisant un schéma, que la probabilité de voir un
système sous une inclinaison  est proportionnelle à
est proportionnelle à 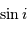 .
.
Difficulté : ☆☆ Temps : 45 min
Cette technique permet la détection de planètes, via la perturbation en vitesse (vitesse réflexe) qu'elles induisent sur leur étoile.
On observe un système constitué d'une planète de masse 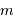 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 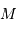 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 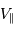 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 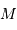 de l'étoile est supposée connue.
de l'étoile est supposée connue.
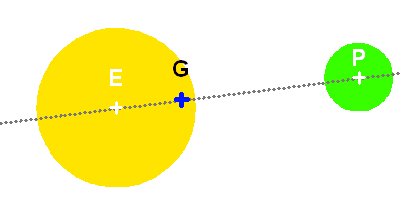
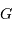 ,
, 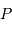 et
et 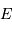 les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
Définir la position du barycentre du système étoile-planète.
Montrer que, dans le référentiel barycentrique, les vitesses 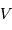 de l'étoile et
de l'étoile et 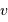 de la planète satisfont à la relation :
de la planète satisfont à la relation :
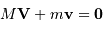
Donner la relation liant 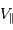 au module
au module 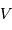 de la vitesse de l'étoile et à l'angle
de la vitesse de l'étoile et à l'angle  entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
Exprimer la 3ème loi de Kepler en fonction des variables 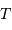 et
et 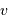 , puis montrer que la masse de la planète s'exprime en fonction des observables
, puis montrer que la masse de la planète s'exprime en fonction des observables 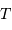 et
et 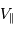 par :
par :