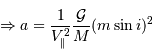Méthode des vitesses radiales
Considérons un système binaire constitué d'une étoile et d'une planète.
Chacun des objets décrit une orbite elliptique dont le foyer est le
centre de masse du système.
Effet Doppler dû à l'oscillation de l'étoile
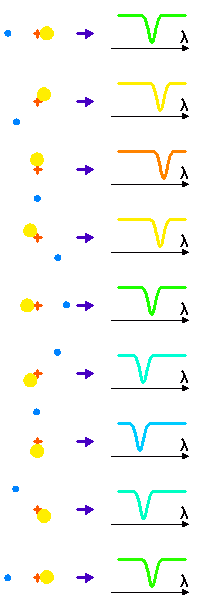
Dans son mouvement, l'étoile tantôt se rapproche, tantôt s'éloigne de l'observateur.
Une raie spectrale est alternativement décalée vers le bleu ou vers le
rouge, selon la vitesse relative entre l'étoile et l'observateur (direction indiquée par une flèche violette).
Crédit :
ASM
Les raies spectrales stellaires qui nous parviennent (à travers un
spectromètre) sont en conséquence tantôt décalées vers le bleu (longueur d'onde plus courte), tantôt vers le rouge (longueur d'onde plus grande), par effet Doppler.
L'orbite de la planète et l'axe de visée
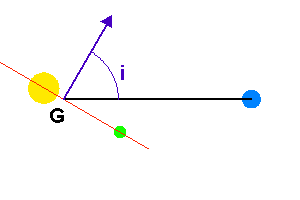
L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
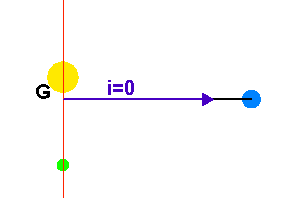
Cas particulier où l'angle

est nul. Pas de mouvement détectable.
Crédit :
ASM
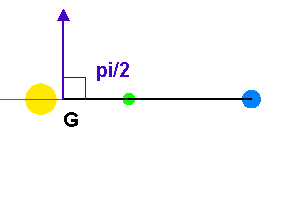
Cas particulier où l'angle

vaut
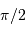
.
Crédit :
ASM
Courbe de vitesse radiale de 51 Peg A
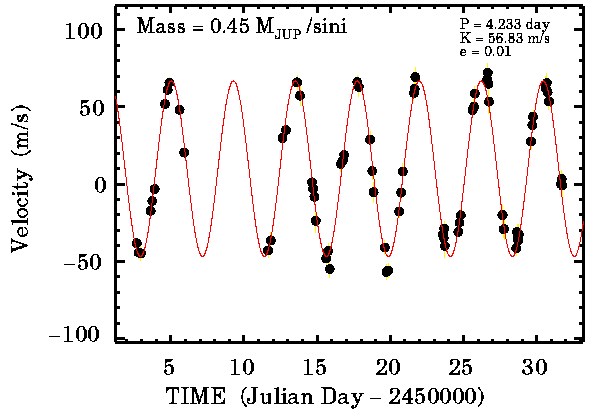
Mesure de vitesse radiale de l'étoile 51Peg.
Crédit :
Butler & Marcy
Vitesse radiale
Animation des mouvements orbitaux planétaires et stellaires, et signature spectrale due à la vitesse radiale de l'étoile.
Effet Doppler dû au mouvement de l'étoile
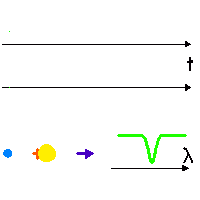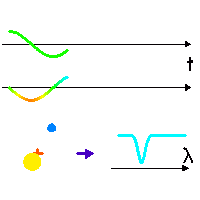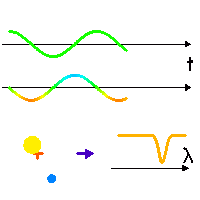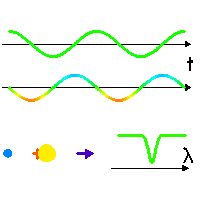
Dans son mouvement (séquence animée), l'étoile en rotation autour du barycentre (croix rouge, fixe) tantôt se rapproche, tantôt s'éloigne (courbe verte) de l'observateur (direction indiquée par la flèche bleu foncé), avec une vitesse donnée par la courbe du milieu (couleur modifiée selon une convention de type
effet Doppler .
Une raie spectrale (courbe du bas) est alternativement décalée vers le bleu ou vers le rouge, selon la vitesse relative entre l'étoile et l'observateur.
Crédit :
ASM

L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
 QCM
QCM
 Le paramètre m sin i
Le paramètre m sin i
Difficulté : ☆☆
Temps : 20 min
On s'intéresse à la distribution du facteur multiplicatif 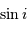 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 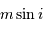 .
.
Question 1)
Rappeler la définition de l'angle 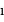 .
.
Question 2)
Statistiquement, trouve-t-on plus de systèmes avec 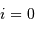 ou bien
ou bien
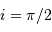 ?
?
Faire un schéma. A quelle condition sur le plan orbital a-t-on
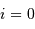 ou
ou 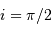 ?
?
Y'a-t-il autant de plans avec 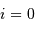 ou
ou 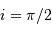 ?
?
Question 3)
Montrer, en faisant un schéma, que la probabilité de voir un
système sous une inclinaison  est proportionnelle à
est proportionnelle à 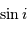 .
.
Question 4)
Calculer la valeur moyenne de 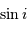 .
.
La définition d'une valeur moyenne conduit à :
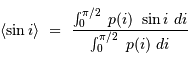
avec 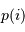 la loi de probabilité associée.
la loi de probabilité associée.
 La vélocimétrie Doppler
La vélocimétrie Doppler
Difficulté : ☆☆
Temps : 45 min
Cette technique permet la détection de planètes, via la perturbation en vitesse (vitesse réflexe) qu'elles induisent sur leur étoile.
On observe un système constitué d'une planète de masse 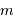 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 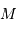 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 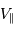 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 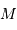 de l'étoile est supposée connue.
de l'étoile est supposée connue.
Schéma du système
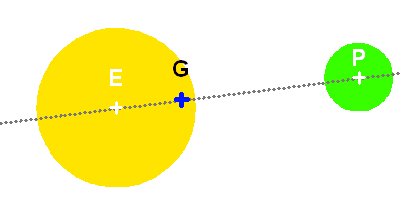
On note respectivement
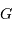
,
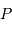
et
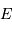
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
Crédit :
ASM
Question 1)
Définir la position du barycentre du système étoile-planète.
Montrer que, dans le référentiel barycentrique, les vitesses 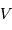 de l'étoile et
de l'étoile et 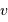 de la planète satisfont à la relation :
de la planète satisfont à la relation :
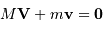
Définir la position du barycentre.
Le barycentre 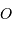 du système obéit à:
du système obéit à:
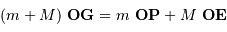
Différencier cette relation pour obtenir l'information en vitesse.
Question 4)
Quelle information inédite apporte cette relation?
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Question 5)
Substituer à l'observable 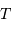 la variable
la variable 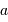 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 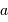 et
et 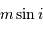 :
:
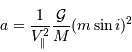
Commencer par réécrire la 3ème loi de Kepler.
- Question 1
Aide :
Revoir le cours !
Solution :
C'est l'angle entre la normale au plan orbital et l'axe de visée.
- Question 2
Aide :
Faire un schéma. A quelle condition sur le plan orbital a-t-on
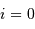 ou
ou 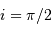 ?
?
Aide :
Y'a-t-il autant de plans avec 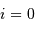 ou
ou 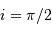 ?
?
Solution :
Il y a un seul plan perpendiculaire à la ligne de visée (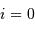 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (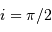 ).
).
- Question 3
Aide :
Il faut estimer toutes les directions  , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 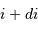 .
.
Solution :
La probabilité est mesurée par l'ouverture du cône de demi-angle
au sommet  . Son angle solide est
. Son angle solide est 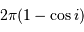 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 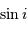 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
La différentielle de l'angle solide aboutit au même résultat.
On retrouve intuitivement que le cas 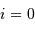 est peu probable.
est peu probable.
- Question 4
Aide :
La définition d'une valeur moyenne conduit à :
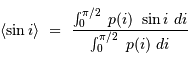
avec 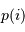 la loi de probabilité associée.
la loi de probabilité associée.
Solution :
Avec 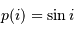 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 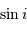 conduit à :
conduit à :
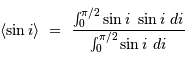
Le numérateur vaut 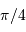 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 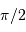 , de
, de 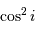 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
Le dénominateur vaut 1.
La valeur moyenne est donc :
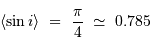
- Question 1
Aide :
Définir la position du barycentre.
Aide :
Le barycentre 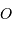 du système obéit à:
du système obéit à:
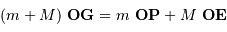
Différencier cette relation pour obtenir l'information en vitesse.
Solution :
Par définition du barycentre, 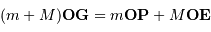 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
Dans le référentiel du centre de masse :
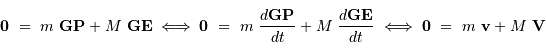
- Question 2
Aide :
Commencer par faire le schéma, pour estimer 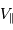 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
Solution :
La relation entre 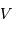 , le module de
, le module de 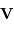 et
et 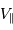 s'écrit :
s'écrit :
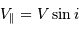
- Question 3
Solution :
La troisième loi de Kepler appliquée à la planète s'écrit :
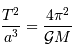
Par ailleurs, la définition du périmètre de l'orbite donne le demi-grand axe en fonction de la période et de la vitesse :
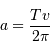
On en déduit :
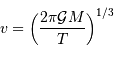
Et on en tire :
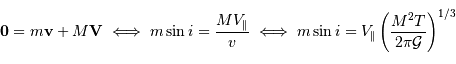
- Question 4
Aide :
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Solution :
A partir des observables, 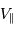 et
et 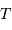 , et de la masse stellaire
, et de la masse stellaire 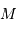 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 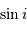 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
- Question 5
Aide :
Commencer par réécrire la 3ème loi de Kepler.
Solution :
La 3ème loi de Kepler... toujours elle, permet d'écrire :
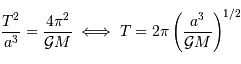
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)
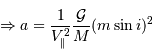


 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.

 est nul. Pas de mouvement détectable.
est nul. Pas de mouvement détectable.

 vaut
vaut 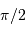 .
.

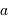 .
.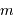 la masse de la planète, et
la masse de la planète, et 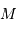 celle de l'étoile.
celle de l'étoile.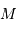 . Mais une variable reste inconnue :
. Mais une variable reste inconnue : 
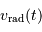 .
Ce type d'observation spectrométrique fournit deux
.
Ce type d'observation spectrométrique fournit deux 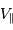 , parallèle à l'axe de visée (car
, parallèle à l'axe de visée (car 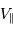 ).
).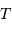 de rotation du système.
de rotation du système.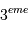 loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
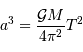
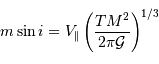
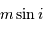 est la masse de la planète
est la masse de la planète 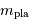 affectée du facteur
géométrique
affectée du facteur
géométrique 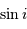 , inconnu.
Le calcul complet est proposé en
, inconnu.
Le calcul complet est proposé en  dépend de l'ouverture du cône de demi-angle au sommet
dépend de l'ouverture du cône de demi-angle au sommet  : elle vaut
: elle vaut 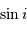 .
La probabilité de voir un système
.
La probabilité de voir un système 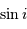 vaut
vaut 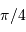 ;
ce calcul est proposé en
;
ce calcul est proposé en 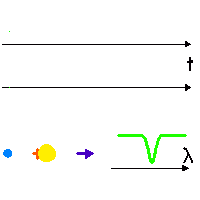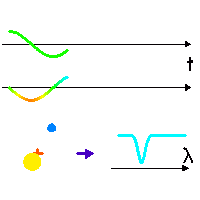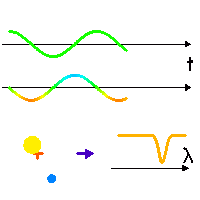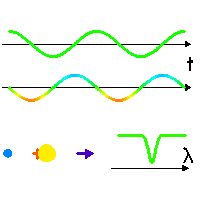
 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
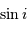 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 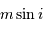 .
.
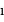 .
.
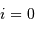 ou bien
ou bien
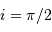 ?
?
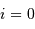 ou
ou 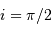 ?
?
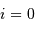 ou
ou 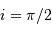 ?
?
 est proportionnelle à
est proportionnelle à 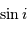 .
.
 , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 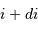 .
.
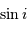 .
.
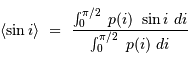
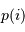 la loi de probabilité associée.
la loi de probabilité associée.
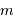 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 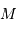 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 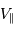 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 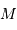 de l'étoile est supposée connue.
de l'étoile est supposée connue.

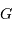 ,
, 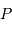 et
et 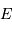 les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
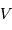 de l'étoile et
de l'étoile et 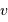 de la planète satisfont à la relation :
de la planète satisfont à la relation :
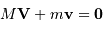
 du système obéit à:
du système obéit à:
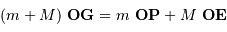
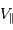 au module
au module 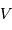 de la vitesse de l'étoile et à l'angle
de la vitesse de l'étoile et à l'angle  entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
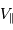 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
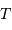 et
et 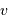 , puis montrer que la masse de la planète s'exprime en fonction des
, puis montrer que la masse de la planète s'exprime en fonction des 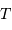 et
et 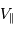 par :
par :
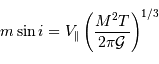
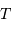 la variable
la variable 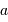 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 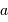 et
et 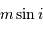 :
:
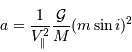
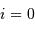 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (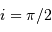 ).
).
 . Son angle solide est
. Son angle solide est 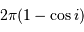 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 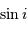 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
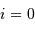 est peu probable.
est peu probable.
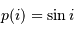 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 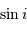 conduit à :
conduit à :
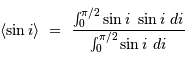
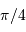 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 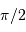 , de
, de 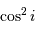 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
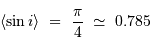
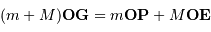 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
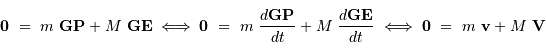
 , le module de
, le module de 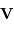 et
et 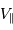 s'écrit :
s'écrit :
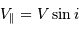
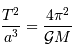
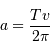
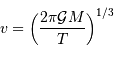
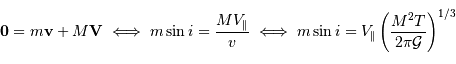
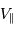 et
et 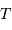 , et de la masse stellaire
, et de la masse stellaire 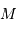 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 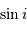 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
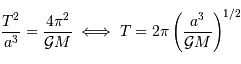
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)