L'effet Doppler-Fizeau est une conséquence directe de la relativité restreinte : la perception d'un signal dépend de la vitesse relative entre la source et le récepteur. En pratique, l'effet Doppler est mis à profit pour mesurer les vitesses radiales de multiples objets, à toutes les échelles dans l'Univers.

Le ciel profond vu par le télescope spatial. Remarquer la corrélation entre la couleur et la luminosité des objets : la lumière des galaxies est décalée vers le rouge suite à l'expansion de l'Univers, et ce d'autant plus qu'elles sont plus lointaines, et donc moins lumineuses.
Crédit :
HST
Décalage spectral
L'effet Doppler module les positions des raies spectrales. En cela, il constitue un traceur de vitesse.

Décalage spectral entre différentes galaxies d'un amas.
Crédit :
ESO
 Objectifs
Objectifs
L'effet Doppler-Fizeau est un effet relativiste, au sens qu'il ne s'explique que dans le cadre de la relativité restreinte. La perception d'un phénomène électromagnétique dépend de la vitesse relative entre la source et le récepteur.
L'effet Doppler
La composante radiale de la vitesse relative entre l'émetteur et l'observateur étant notée 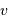 , comptée positivement pour un éloignement de la source au récepteur, l'effet Doppler relie la longueur d'onde reçue
, comptée positivement pour un éloignement de la source au récepteur, l'effet Doppler relie la longueur d'onde reçue 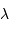 à la longueur d'onde émise
à la longueur d'onde émise 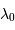 par :
par :
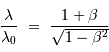
avec la notation relativiste usuelle du terme 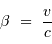 .
.
Le terme 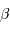 au numérateur correspond à la translation relative entre l'émetteur et l'observateur ; le dénominateur introduit la correction relativiste.
Pour des vitesses non relativistes (typiquement inférieures à c/10), les termes d'ordre supérieur à
au numérateur correspond à la translation relative entre l'émetteur et l'observateur ; le dénominateur introduit la correction relativiste.
Pour des vitesses non relativistes (typiquement inférieures à c/10), les termes d'ordre supérieur à 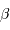 sont négligeables et l'on a simplement :
sont négligeables et l'on a simplement :
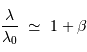
soit le décalage :
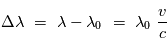
Un éloignement rougit la longueur d'onde perçue, un rapprochement la
bleuit.
Effet Doppler : principe
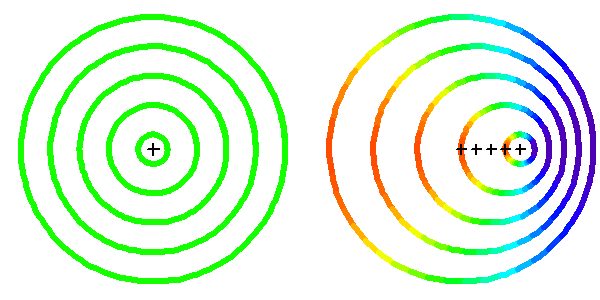
Selon la direction de visée, l'observateur verra ou non la modulation Doppler du rayonnement de la source en mouvement.
Crédit :
ASM
Effet radial
A faible vitesse, l'effet Doppler est du 1er ordre dans sa composante radiale, mais du 2e ordre en vitesse transversale.
 Effet Doppler sismique
Effet Doppler sismique
Difficulté : ☆
Temps : 5 min
Question 1)
Pourquoi l'animation du champ de vitesse Doppler montre-t-elle un gradient de vitesse dans la photosphère ?
Quelle composante de la vitesse est sensible à l'effet Doppler ?
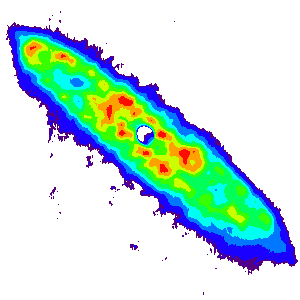
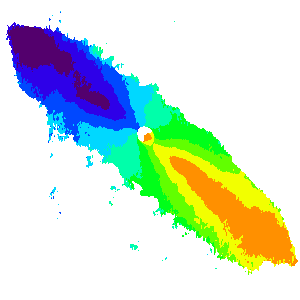
Abondance de l'hydrogène atomique neutre dans la galaxie NGC 253 ; et tracé du champ de vitesse galactique via les modulations de la position de la raie étudiée
Crédit :
IRAM
Champ de vitesse galactique
L'abondance en hydrogène atomique dans une galaxie peut être mesurée par l'observation de raies de l'hydrogène  . Ces raies étant modulées par la vitesse relative entre la source et l'observateur, la mesure de la modulation donne accès au champ de vitesse de l'hydrogène dans la galaxie.
. Ces raies étant modulées par la vitesse relative entre la source et l'observateur, la mesure de la modulation donne accès au champ de vitesse de l'hydrogène dans la galaxie.
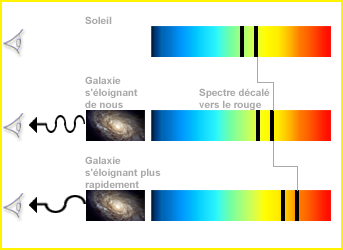

Décalage vers le rouge de raies de galaxies lointaines entraînées par l'expansion de l'Univers. Principe, et observation historique par l'astronome américain Humason.
Crédit :
ASM et Hale Observatories
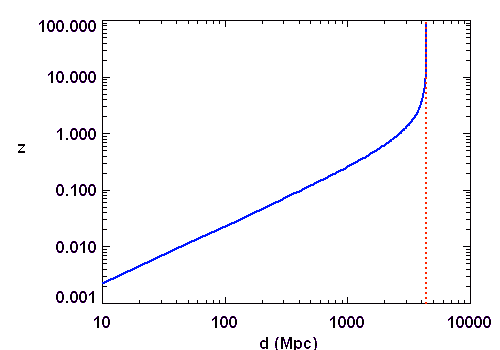
Distance et décalage spectral.
Crédit :
ASM
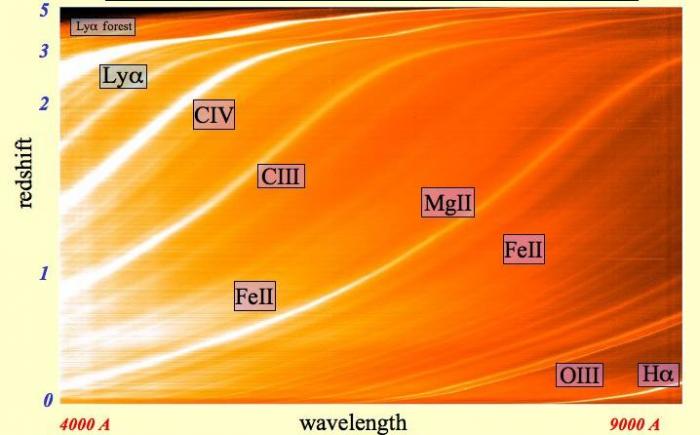
Relevé des décalages spectraux de 46420 quasars observés par le grand relevé
SDSS, sondant des quasars avec des décalages spectraux jusqu'à 5. On note le très grand déplacement des diverses raies identifiées.
Crédit :
SDSSIII
Expansion de l'Univers
Historiquement, la vitesse de fuite des objets lointains, due à l'expansion de l'Univers, a été mise en évidence par le décalage vers le rouge de leurs raies spectrales. Ce décalage augmente avec la distance, selon la loi de Hubble.
C'est ainsi que l'on peut aujourd'hui sonder l'Univers à grande échelle avec les quasars.
 Objectifs
Objectifs
Les champs d'application pratiques de l'effet Doppler en astrophysique sont nombreux :
forts décalages spectraux (ex : loi de Hubble) ;
modulation d'un champ de vitesse, temporelle (ex : astérosismologie)
ou spatiale (ex : champ de rotation galactique).
L'effet Doppler : traceur de vitesses
L'effet Doppler
permet de mesurer des vitesses radiales, càd alignées sur la ligne de visée.
Si l'on dispose d'une observable spectrale
adéquate, on bénéfie par l'effet Doppler d'un traceur de vitesse,
l'effet Doppler reliant la longueur d'onde reçue 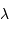 à la longueur d'onde émise
à la longueur d'onde émise 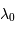 par :
par :
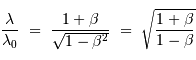
avec la définition usuelle : 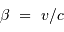 .
.
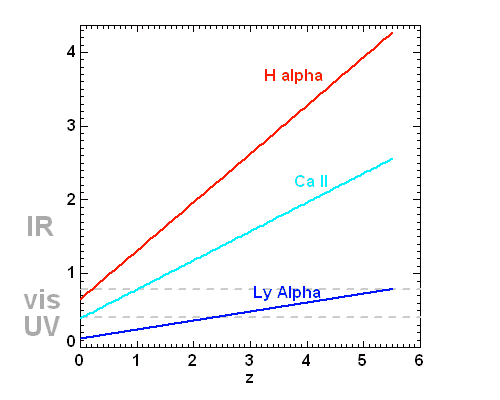
Déplacement de quelques raies en fonction du décalage spectral.
Crédit :
ASM

Image et zoom sur l'objet IOK-1 présentant un décalage spectral z de 6.96. Le traitement des couleurs le fait apparaître extrêmement rougi.
Crédit :
Télescope SUBARU
Décalage spectral
On note 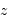 le décalage vers le rouge des objets lointains ("redshift"). Sa définition est relié à la translation en longueur d'onde :
le décalage vers le rouge des objets lointains ("redshift"). Sa définition est relié à la translation en longueur d'onde :
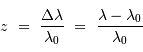
Ceci conduit par exemple au déplacement vers le visible de la raie 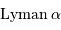 d'objets très lointains.
d'objets très lointains.
Fin 2008, le plus grand décalage spectral mesuré approche la valeur 7. En 2009, l'observation d'une éruption gamma par le satellite Swift de la NASA fut suivie par l'observation à l'ESO du spectre infrarouge de l'objet en cause, qui a mis en évidence un décalage spectral de 8.2. Ce décalage correspondrait à un objet observé dans l'Univers âgé de seulement 600 millions d'années.
Effet Doppler et mesure de vitesse radiale
Voir la page dédiée aux exoplanètes.
Effet Doppler et sismologie
L'astérosismologie étudie la propagation d'ondes mécaniques (ondes sonores, ondes de gravité) dans l'intérieur d'une étoile. Le champ de vitesse sismique dans la photosphère stellaire module les raies spectrales, comme le montre l'animation ci-contre.
Remarquer que vitesse d'oscillation et amplitude sont en quadrature. Les amplitudes et les couleurs codant la modulation par effet Doppler sont très exagérées.
Effet Doppler et sismologie

Amplitude (courbe et image en jaune) et vitesse d'oscillation. Une raie du spectre stellaire est modulée par effet Doppler. Le code des couleurs signale par un rougissement un éloignement, et par un bleuissement un rapprochement.
Crédit :
ASM
Saturne et ses anneaux
A l'aide de l'appliquette, estimer la vitesse de rotation de Saturne, ainsi que la vitesse moyenne des anneaux.
Le spectre a été obtenu en lumière solaire réfléchi, avec un fente sélectionnant la région équatoriale de Saturne et les anneaux de part et d'autre. Les raies d'émission en bordure du spectre correspondent à une lampe spectrale de référence.

 Chaud devant !
Chaud devant !
Difficulté : ☆
Temps : 25 min
Le fond cosmologique présente actuellement une température de l'ordre de 3 K, alors qu'elle était de 3000 K à l'époque de la recombinaison. A cette époque, les électrons et les protons se sont recombinés pour former les atomes neutres d'hydrogène. Avant, l'agitation thermique liée à des températures plus élevées interdisait cette recombinaison et l'Univers était un plasma principalement composé de protons et d'électrons.
Question 1)
Déterminer le décalage spectral 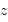 à l'époque de la recombinaison.
à l'époque de la recombinaison.
Appliquer d'abord la loi de déplacement de Wien
Question 2)
Déterminer le facteur 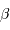 correspondant.
correspondant.
Application directe du cours
 Dispersion de vitesse
Dispersion de vitesse
Difficulté : ☆
Temps : 25 min
Le spectre ci-joint montre les raies de 7 galaxies différentiellement dispersées.
Spectres de galaxies 
Question 1)
Etalonner le spectre, en pm/pixel, en sachant que les 3 raies principales sont identifiées à 580.0, 582.1 et 585.5 nm.
Procéder par règle de 3, avec l'outil proposé.
Question 2)
En déduire l'échelle en 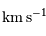 par pixel.
par pixel.
Application directe du cours
Question 3)
En déduire les dispersion en vitesse radiale de chacune des galaxies, par rapport au groupe des 3 galaxies homocinétiques.
 Raie à 21 cm
Raie à 21 cm
Difficulté : ☆
Temps : 25 min
Le spectre ci-joint montre la raie à 21 cm de l'hydrogène d'une galaxie lointaine s'éloignant du Soleil. L'axe des abscisses suppose, ici, qu'une vitesse négative correspond à un éloignement.
Raie à 21 cm
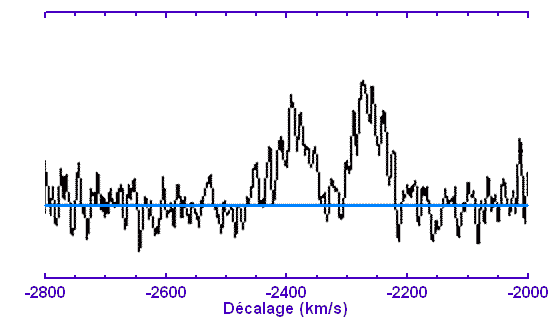
Les 2 composantes de la raies correspondent aux ailes de la galaxie, en rotation, se rapprochant et s'éloignant de l'observateur.
Crédit :
ASM
Question 1)
Estimer la vitesse d'éloignement global de cette galaxie, puis sa distance
(avec 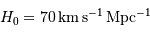 ).
).
[2 points]
Question 2)
A quelle position a été mesurée pour cette galaxie la raie 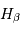 (au repos : 486 nm) ?
(au repos : 486 nm) ?
[1 points]
Question 3)
Estimer la vitesse de rotation moyenne de la galaxie (en précisant le critère de mesure).
[1 points]
 Quasar lointain
Quasar lointain
Difficulté : ☆
Temps : 10 min
Le spectre ci-joint montre la raie Lyman alpha d'un quasar très lointain (longueur d'onde au repos : 121.6 nm). Abscisse : longueur d'onde en nm ; ordonnée : flux en unité arbitraire.

Question 1)
Estimer le décalage spectral de ce quasar.
[1 points]
Question 2)
Traduire le décalage spectral en vitesse d'éloignement.
[1 points]
 Forêt Lyman-alpha
Forêt Lyman-alpha
Difficulté : ☆
Temps : 30 min
Les quasars sont des sources extrêmement lumineuses et éloignées (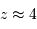 ), de diamètre apparent non-mesurable. Elles émettent un spectre continu, avec peu de raies d'émission. Les nuages de gaz intergalactique froid se trouvant sur la ligne de visée signent leur présence par un spectre de raies d'absorption.
), de diamètre apparent non-mesurable. Elles émettent un spectre continu, avec peu de raies d'émission. Les nuages de gaz intergalactique froid se trouvant sur la ligne de visée signent leur présence par un spectre de raies d'absorption.
Le constituant principal de ce gaz intergalactique étant l'hydrogène, dont le spectre est parfaitement connu (raies 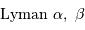 , ...) rend possible l'identification pour chaque nuage, de son décalage spectral
, ...) rend possible l'identification pour chaque nuage, de son décalage spectral 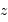 et sa profondeur optique. Il faut évidemment pour cela un spectromètre à haute résolution.
et sa profondeur optique. Il faut évidemment pour cela un spectromètre à haute résolution.
Le quasar HE 2217-2818 présente une forêt de raies en absorption (voir l'appliquette basée sur des données de l'instrument UVES du VLT, avec en abscisse la longueur d'onde en nm et en ordonnée le flux en unité arbitraire), correspondant aux nuages d'hydrogène rencontrés sur la ligne de visée.

Question 1)
Déterminer les principales raies d'absorption, et en déduire les décalages spectraux 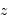 de ces nuages, en supposant que la raie au repos est la raie
de ces nuages, en supposant que la raie au repos est la raie
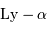 de longueur d'onde au repos
de longueur d'onde au repos 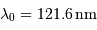 . En déduire les vitesses de fuite.
. En déduire les vitesses de fuite.
[3 points]
Question 2)
Quelle information apporte la profondeur optique du nuage (retranscrite par la profondeur de la raie), et que peut-on en tirer ?
[2 points]
Elargissement rotationnel
La rotation de l'étoile mélange, sauf à résoudre spatialement ou spectralement l'objet, les diverses régions qui toutes contribuent au flux stellaire. Il s'ensuit un élargissement des raies.


La rotation de l'étoile, en codage Doppler : une couleur rouge signe un éloignement radial ; le bleu un rapprochement. Un axe de rotation quasi perpendiculaire au plan du ciel entraîne une très faible signature, car la projection géométrique amoindrit la composante radiale de la vitesse de rotation.
Crédit :
ASM
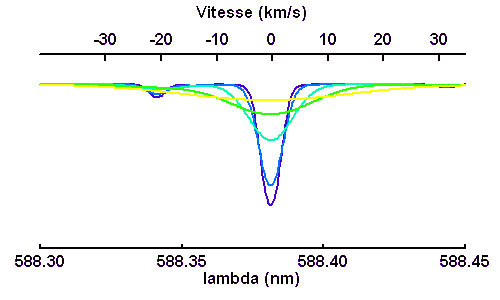
Elargissement rotationnel (vitesse équatoriale de 1, 2, 5, 10, 20 ou 40 km/s. La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
Crédit :
ASM
Elargissement en température et rotationnel
L'élargissement des raies due à la rotation de l'étoile modifie drastiquement l'allure d'un spectre, comme le montre les simulations d'observation à
faible ou
grande résolution spectrale.
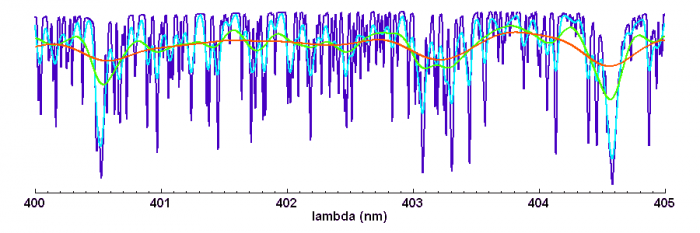
Elargissement rotationnel (
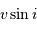
de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)
Crédit :
ASM
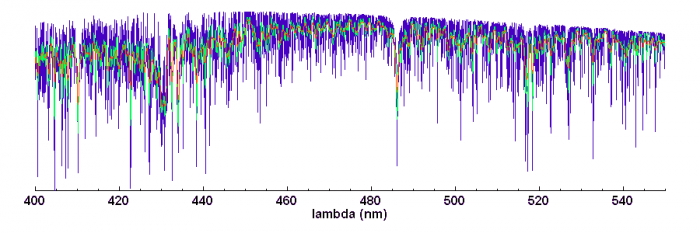
Elargissement rotationnel (
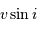
de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
Crédit :
ASM
 Objectifs
Objectifs
La largeur des raies stellaires est liée aux champs de vitesse Doppler.
Agitation thermique
Dans le cadre de la théorie cinétique du gaz parfait, la distribution de vitesse est donnée par :
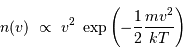
avec 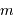 la masse atomique moyenne et
la masse atomique moyenne et 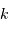 la constante de Boltzmann.
la constante de Boltzmann.
La largeur à mi-hauteur de cette distribution est de l'ordre de 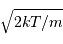 , du même ordre de grandeur que les vitesses moyenne ou la plus probable.
, du même ordre de grandeur que les vitesses moyenne ou la plus probable.
Avec une température stellaire entre typiquement 4000 et 40000 K, les vitesses
d'agitation thermique sont de l'ordre de 8 à 25 km/s : elles concourent à un sensible élargissement des raies.
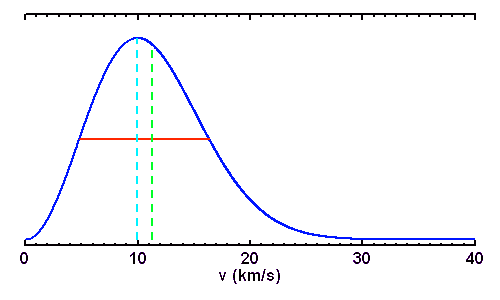
Distribution de vitesse de Boltzman. La vitesse la plus probable (bleu clair) est voisine de la vitesse moyenne (vert), et elles sont toutes deux du même ordre de grandeur que la dispersion caractéristique en vitesse (rouge).
Crédit :
ASM
Rotation stellaire
La rotation stellaire participe également à l'élargissement des raies stellaires.
Le paramètre important pour mesurer cet effet est donné par la projection du vecteur vitesse de rotation équatorial sur la ligne de visée :
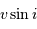 .
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
.
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
En effet, une raie fine à vitesse rotationnelle non nulle s'élargit par effet Doppler. Par application de la conservation de l'énergie, le manque de photons dans la raie est conservé, et donc l'élargissement de la raie s'accompagne d'une moindre profondeur.
Élargissement des raies stellaires selon la vitesse de rotation stellaire
La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
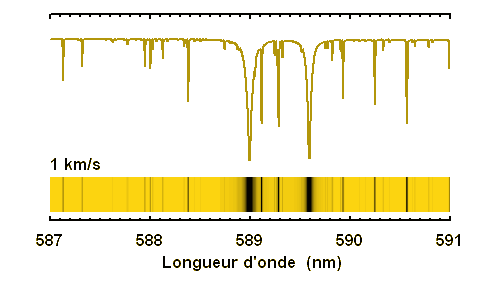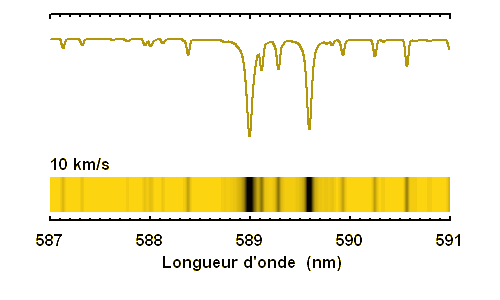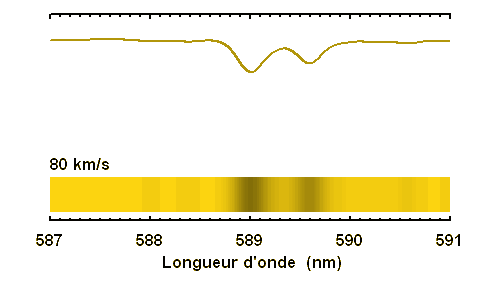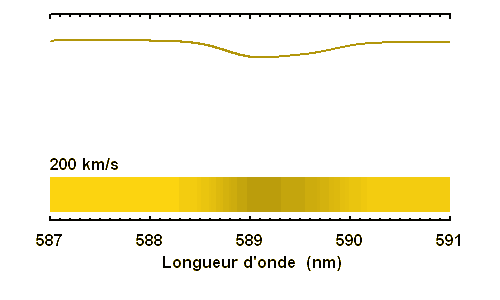
La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
Crédit :
ASM
Elargissement des raies stellaires selon la direction de l'inclinaison
L'animation montre comme varie l'élargissement rotationnel des raies stellaires avec l'angle d'inclinaison  . Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
. Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
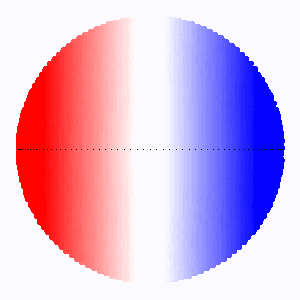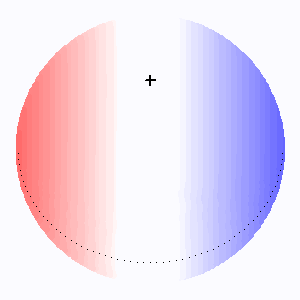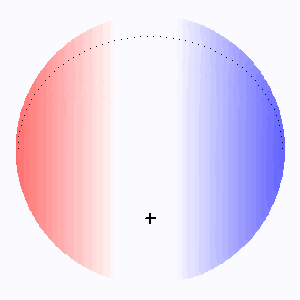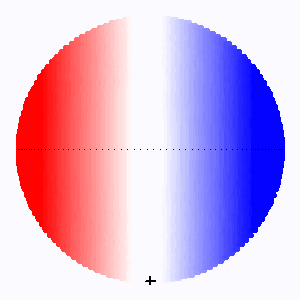
L'élargissement rotationnel (codé ici en couleur d'autant plus rouge/bleue que la vitesse d'éloignement/rapprochement est grande) dépend du facteur
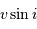
, et varie ici avec l'inclinaison

sur l'axe de visée.
Crédit :
ASM
Mesure de rotation par sondage radar
Les sondages radar permettent de mesurer la rotation d'un corps, comme le montre l'animation ci-jointe.
L'onde plane incidente parcourt l'objet du point subterrestre jusqu'au limbe, en une durée 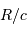 (
(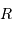 est le rayon de l'objet,
est le rayon de l'objet, 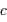 la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
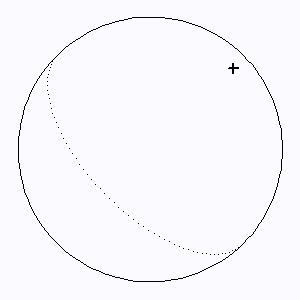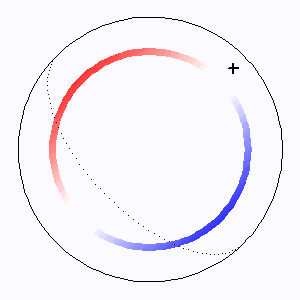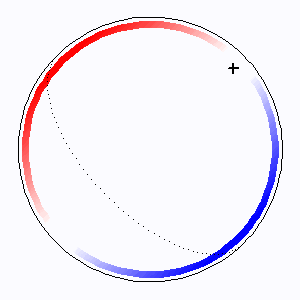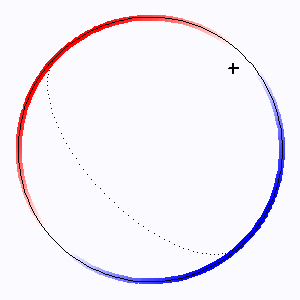
Sondage d'un objet, supposé sphérique, par une onde plane radar. L'animation suppose un pas de temps équidistant. Les premières mesures, en projection sur le plan du ciel, parcourent
rapidement l'objet, plus lentement ensuite pour les régions proches du limbe, mais alors l'excursion en vitesse Doppler devient maximale
Crédit :
ASM
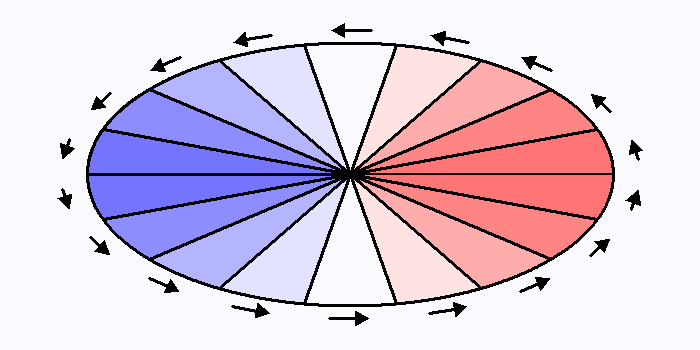
Disque en rotation.
Crédit :
ASM
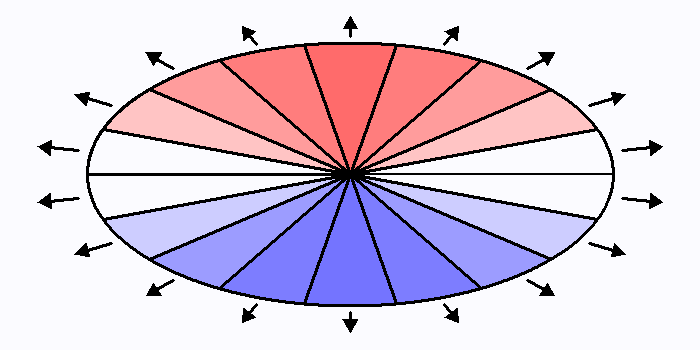
Disque en expansion
Crédit :
ASM
 Mesure de la période de rotation de Mercure
Mesure de la période de rotation de Mercure
Difficulté : ☆☆
Temps : 1.5 heure
Le but de l'exercice est d'interpréter les observations radio de la planète Mercure, menées au radio-télescope d'Arecibo en 1965
(Dyce et al. 1965, Astronomical Journal 72, 351-359). Il s'agissait alors de mesurer la période de rotation propre de Mercure, et de déterminer si elle était égale ou non à la période de rotation orbitale.
| demi-grand axe | 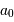 | 0.39 UA |
| révolution sidérale | 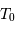 | 88 j |
| rayon | 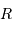 | 2420 km |
| diamètre du radiotél. | 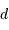 | 305 m |
| fréquence émise | 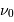 | 430 MHz |

Question 1)
Propagation :
L'écho d'un signal radio émis par le télescope d'Arecibo et
réfléchi par Mercure est réceptionné 616.125 s après son
émission. En déduire la distance Terre-Mercure 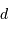 lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
L'onde radio parcourt le vide à la célérité de la lumière.
Attention au doublement de la distance par aller-retour.
Question 4)
L'écho :
Le document ci-joint (Dyce et al. 1965)
montre l'étalement en fréquence de l'écho en
fonction du retard à la réception.
Comparer le retard maximal théorique à celui enregistré, et interpréter
le désaccord. En déduire, que la relation entre 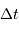 et
et 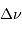 se réduit, pour les mesures effectuées, à
se réduit, pour les mesures effectuées, à 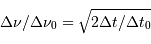 Comment interpréter les variations temporelles d'intensité du signal ?
Comment interpréter les variations temporelles d'intensité du signal ?
Estimer 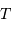 , la période de rotation propre de Mercure.
, la période de rotation propre de Mercure.
On pose 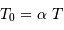 . Quelle signification donner à
. Quelle signification donner à 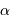 ?
De quelle fraction simple
?
De quelle fraction simple 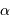 est-il proche ? Est-ce un hasard ?
est-il proche ? Est-ce un hasard ?
Pourquoi les données présentant un plus fort retard ne sont-elles pas
facilement exploitables ?
Etudier les conditions de réflexion de l'onde, en supposant valide l'optique géométrique.
Montrer que les dates effectives d'observations vérifient 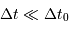 , et en tirer les conséquences.
, et en tirer les conséquences.
Question 5)
La puissance de l'écho :
Quelle fraction du signal Mercure intercepte-t-il ? [on se contentera d'un ordre de grandeur grossier, en supposant que le flux radar est homogène dans un champ d'angle solide égal au lobe principal de diffraction ; un calcul précis est hors de portée de la modélisation proposé].
Estimer, à l'aide d'un modèle simple, le nombre de photons incidents nécessaires pour réceptionner 1 photon en retour après réflexion au point subterrestre.
Une puissance d'émission de 2 MW vous étonne-t-elle ?
[l'impulsion radar incidente est très brève : 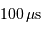 ; on se contentera également d'un ordre de grandeur grossier]
; on se contentera également d'un ordre de grandeur grossier]
La diffraction conduit à un lobe d'antenne de taille angulaire commensurable 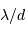 .
.
Pour le flux réfléchi : proposer un modèle simple pour les conditions de réflexion au point subterrestre.
 Spectres observé et théorique
Spectres observé et théorique
Difficulté : ☆
Temps : 10 min
La figure ci-jointe donne une portions des spectres observé et théorique d'une étoile de type F2, classe V.
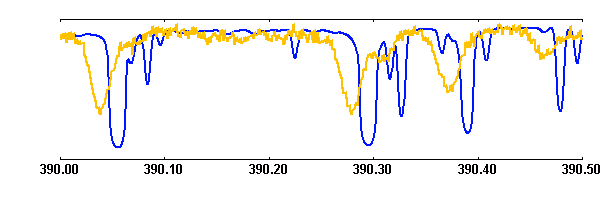
Spectres théorique (bleu) et observé (orange)
Crédit :
ESO/ASM
Question 1)
Expliquer les différences entre les 2 spectres
[1 points]
Question 2)
Donner un ordre de grandeur de 2 vitesses caractéristiques du spectre observé.
[2 points]
Retenir de cette section les multiples domaines où l'effet Doppler-Fizeau influence très sensiblement la signature spectrale des objets. Comme à l'accoutumée, les astrophysiciens en ont tiré parti pour avoir accès à des observables inaccessibles par ailleurs.
La relation 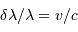 (à faible vitesse) est tellement prégnante que l'on peut très bien, en l'appliquant, définir une grandeur spectrale en vitesse et non en longueur d'onde.
(à faible vitesse) est tellement prégnante que l'on peut très bien, en l'appliquant, définir une grandeur spectrale en vitesse et non en longueur d'onde.
L'utilisation de l'effet Doppler pour avoir accès à la cinématique des objets a motivé le développement de différentes catégories de spectromètres (voir la section dédiée à l'instrumentation).

- Question 1
Aide :
Procéder par règle de 3, avec l'outil proposé.
Solution :
Les raies sont repérées aux positions (en pixel) :
132, 178, 253
Les intervalles spectraux, respectivement de 2100 et 5500 pm entre les raies 1 et 2 puis 1 et 3, correspondent à une mesure de 46 et 121 pixels.
La conversion et donc de l'ordre de l'ordre de 45.5 pm/px.
- Question 2
Aide :
Application directe du cours
Solution :
A 582 nm, un décalage de 45.5 pm représente une vitesse 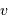 telle que :
telle que :
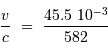
Soit environ 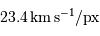 .
.
- Question 3
Solution :
Les décalages spectraux mesurent respectivement, en pixels :
-10, +3, +14, -6.
D'où les décalages en vitesse de -230, 70, 330, -140 km/s
- Question 1
Aide :
L'onde radio parcourt le vide à la célérité de la lumière.
Attention au doublement de la distance par aller-retour.
Solution :
Un trajet de 616.125 s correspond à une distance aller-retour de 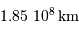 , soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
, soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
Dans ces conditions, Mercure est trop proche du Soleil pour être observé en lumière visible.
- Question 2
Aide :
Faire un schéma
Aide :
Un point 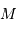 possède une vitesse de rotation
possède une vitesse de rotation 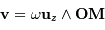
Solution :
La vitesse d'entraînement rotationnel vérifie :
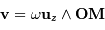
avec 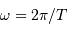 la rotation angulaire.
la rotation angulaire.
Soit, pour un point de coordonnées cartésiennes 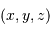 (avec bien sûr
(avec bien sûr 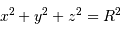 :
:
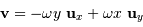
La projection radiale est la composante selon 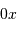 , càd
, càd 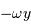
- Question 3
Aide :
Faire un schéma, avec les axes indiqués.
S'inspirer de l'animation sondage rotationnel .
Dans les applications numériques, ne pas oublie un facteur 2 temporel (aller-retour de l'onde) ou fréquentiel (double décalage Doppler à l'absorption et à la réémission de l'onde)
Solution :
La région de la surface hermienne contribuant au début du signal d'écho est le point le plus proche de la Terre : le point subterrestre. La fin correspond aux dernières régions touchées : au limbe.
La durée totale théorique 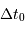 de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
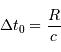
Les lignes d'iso-retard 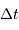 sur la carte
de Mercure [
sur la carte
de Mercure [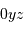 ] sont des lignes à coordonnée
] sont des lignes à coordonnée 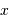 fixée. Analytiquement, à la surface de la planète et dans le plan du ciel
fixée. Analytiquement, à la surface de la planète et dans le plan du ciel 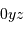 , l'équation
, l'équation
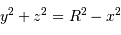
représente un cercle.
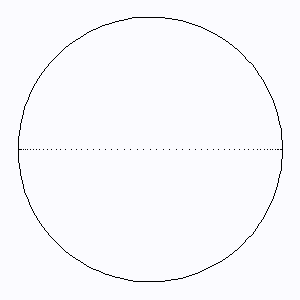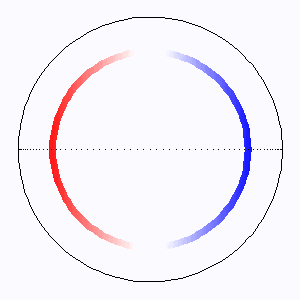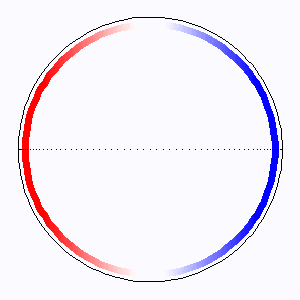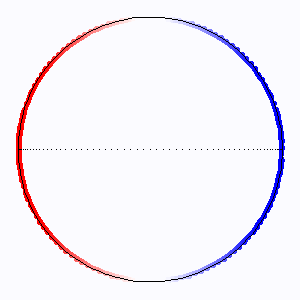
L'élargissement Doppler extrêmal est atteint au limbe, où l'entraînement rotationnel est le plus fort.
Les lignes d'iso-fréquence correspondent aux lignes isovitesses : ce sont des droites parallèles à l'axe de rotation.
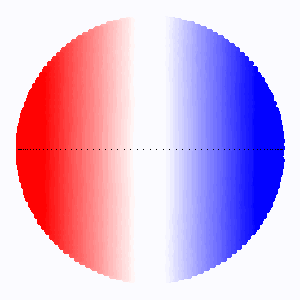 Pour un point de Mercure de coordonnées
Pour un point de Mercure de coordonnées
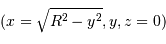 , le retard
, le retard 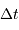 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 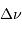 vérifient :
vérifient :
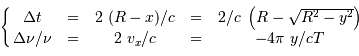
Les valeurs extrêmes du délai et du décalage sont :
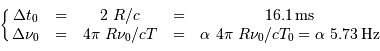
en ayant posé  .
On en déduit, pour un point du plan équatorial (
.
On en déduit, pour un point du plan équatorial (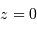 ) :
) :
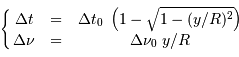
En éliminant la variable 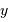 , il sort la relation demandée :
, il sort la relation demandée :
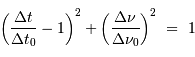
- Question 4
Aide :
Etudier les conditions de réflexion de l'onde, en supposant valide l'optique géométrique.
Aide :
Montrer que les dates effectives d'observations vérifient 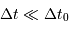 , et en tirer les conséquences.
, et en tirer les conséquences.
Aide :
Pour calculer 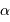 avec l'appliquette, la relation entre
avec l'appliquette, la relation entre 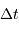 et
et 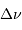 se traduit par :
= (B1/5.73) * sqrt(16.1 / (2*A1)), à faire calculer en ayant sélectionné la case C1
se traduit par :
= (B1/5.73) * sqrt(16.1 / (2*A1)), à faire calculer en ayant sélectionné la case C1
Solution :
Le retard maximal théorique est bien plus long que celui enregistré. Le
désaccord s'interprète par l'absence de signal réfléchi dans les régions proches du limbe.
Les lois de l'optique géométrique permettent d'interpréter les variations temporelles d'intensité du signal : la réflexion renvoie de moins en moins d'énergie vers la Terre dès lors que le signal s'éloigne du point subterrestre.
Et donc, les données présentant un grand retard par rapport au point subterrestre ne pas exploitables.
Les dates effectives d'observations vérifient alors 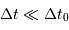 . Il s'ensuit que la relation entre
. Il s'ensuit que la relation entre 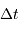 et
et 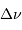 se simplifie en
se simplifie en
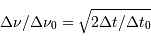
en ayant procédé au développement limité : 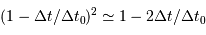 . Il en sort l'estimation de
. Il en sort l'estimation de 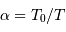 :
:
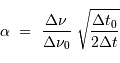
A l'aide de l'appliquette, on trouve 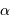 de l'ordre de 1.65, voisin de 5/3.
de l'ordre de 1.65, voisin de 5/3. 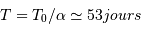 .
.
La rotation propre de Mercure est en résonance avec la révolution autour du Soleil. Mais elle est ici mesurée dans le référentiel tournant : la rotation propre sidérale découle du changement de référentiel, ici mesurée avec pour unité la révolution sidérale :
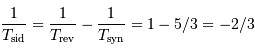
La rotation sidérale propre est plus lente que la révolution sidérale, est dans un rapport 3/2.
- Question 5
Aide :
La diffraction conduit à un lobe d'antenne de taille angulaire commensurable 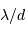 .
.
Aide :
Pour le flux réfléchi : proposer un modèle simple pour les conditions de réflexion au point subterrestre.
Solution :
La diffraction conduit à un lobe d'antenne de taille angulaire 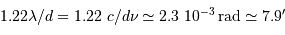 . En regard, Mercure intercepte une fraction angulaire
. En regard, Mercure intercepte une fraction angulaire 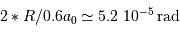 . La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit
. La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit 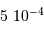 .
.


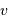 , comptée positivement pour un éloignement de la source au récepteur, l'effet Doppler relie la longueur d'onde reçue
, comptée positivement pour un éloignement de la source au récepteur, l'effet Doppler relie la longueur d'onde reçue 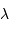 à la longueur d'onde émise
à la longueur d'onde émise 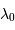 par :
par :
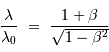
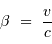 .
.
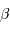 au numérateur correspond à la translation relative entre l'émetteur et l'observateur ; le dénominateur introduit la correction relativiste.
Pour des vitesses non relativistes (typiquement inférieures à c/10), les termes d'ordre supérieur à
au numérateur correspond à la translation relative entre l'émetteur et l'observateur ; le dénominateur introduit la correction relativiste.
Pour des vitesses non relativistes (typiquement inférieures à c/10), les termes d'ordre supérieur à 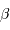 sont négligeables et l'on a simplement :
sont négligeables et l'on a simplement :
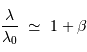
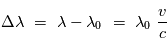

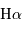 , au repos à 656.3 nm.
, au repos à 656.3 nm.


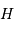 . Ces raies étant modulées par la vitesse relative entre la source et l'observateur, la mesure de la
. Ces raies étant modulées par la vitesse relative entre la source et l'observateur, la mesure de la 



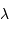 à la longueur d'onde émise
à la longueur d'onde émise 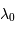 par :
par :
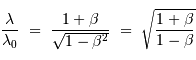
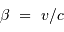 .
.


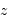 le décalage vers le rouge des objets lointains ("redshift"). Sa définition est relié à la translation en longueur d'onde :
le décalage vers le rouge des objets lointains ("redshift"). Sa définition est relié à la translation en longueur d'onde :
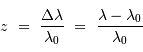
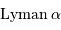 d'objets très lointains.
d'objets très lointains.


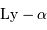 du quasar PKS 2000-330 est observée à la longueur d'onde
du quasar PKS 2000-330 est observée à la longueur d'onde 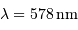 , et non à la longueur d'onde au repos
, et non à la longueur d'onde au repos 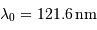 .
.
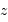 de ce quasar, ainsi que son facteur relativiste
de ce quasar, ainsi que son facteur relativiste 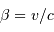 .
.
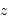 à
à 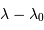 ... allez, on est sympa :
... allez, on est sympa :
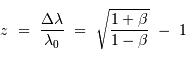
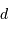 , en appliquant la relation de Hubble
, en appliquant la relation de Hubble 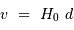 .
avec
.
avec 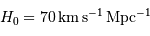 .
.
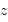 à l'époque de la recombinaison.
à l'époque de la recombinaison.
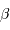 correspondant.
correspondant.
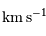 par pixel.
par pixel.

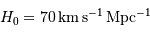 ).
).
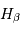 (au repos : 486 nm) ?
(au repos : 486 nm) ?
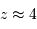 ), de diamètre apparent non-mesurable. Elles émettent un spectre continu, avec peu de raies d'émission. Les nuages de gaz intergalactique froid se trouvant sur la ligne de visée signent leur présence par un spectre de raies d'absorption.
), de diamètre apparent non-mesurable. Elles émettent un spectre continu, avec peu de raies d'émission. Les nuages de gaz intergalactique froid se trouvant sur la ligne de visée signent leur présence par un spectre de raies d'absorption.
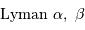 , ...) rend possible l'identification pour chaque nuage, de son décalage spectral
, ...) rend possible l'identification pour chaque nuage, de son décalage spectral 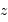 et sa profondeur optique. Il faut évidemment pour cela un spectromètre à haute résolution.
et sa profondeur optique. Il faut évidemment pour cela un spectromètre à haute résolution.
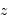 de ces nuages, en supposant que la raie au repos est la raie
de ces nuages, en supposant que la raie au repos est la raie
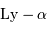 de longueur d'onde au repos
de longueur d'onde au repos 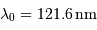 . En déduire les vitesses de fuite.
. En déduire les vitesses de fuite.




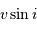 de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)
de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)

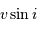 de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
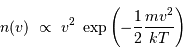
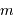 la masse atomique moyenne et
la masse atomique moyenne et 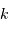 la constante de Boltzmann.
la constante de Boltzmann.
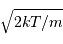 , du même ordre de grandeur que les vitesses moyenne ou la plus probable.
, du même ordre de grandeur que les vitesses moyenne ou la plus probable.

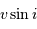 .
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
.
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.

 . Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
. Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.

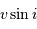 , et varie ici avec l'inclinaison
, et varie ici avec l'inclinaison  sur l'axe de visée.
sur l'axe de visée.
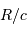 (
(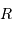 est le rayon de l'objet,
est le rayon de l'objet, 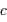 la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.



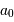
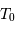
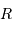
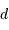
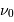
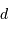 lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
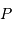 de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
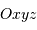 , où
, où 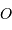 est le barycentre de la planète,
est le barycentre de la planète,
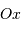 pointe vers la Terre et
pointe vers la Terre et 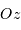 est parallèle à l'axe de rotation de la
planète. On note
est parallèle à l'axe de rotation de la
planète. On note 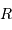 le rayon de la planète Mercure,
le rayon de la planète Mercure, 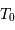 sa période de révolution sidérale, et
sa période de révolution sidérale, et 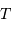 sa période de rotation propre.
sa période de rotation propre.
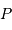 .
.
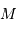 possède une vitesse de rotation
possède une vitesse de rotation 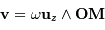
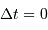 ) et à la fin (
) et à la fin (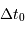 ) du signal d'écho.
Déterminer la durée totale théorique
) du signal d'écho.
Déterminer la durée totale théorique 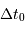 de l'écho ?
Représenter l'allure des lignes d'iso-retard
de l'écho ?
Représenter l'allure des lignes d'iso-retard 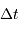 sur la carte
de Mercure [
sur la carte
de Mercure [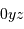 ].
].
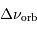 le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
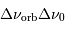 du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence
du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence 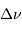 (à
(à 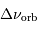 près).
près).
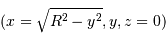 , le retard
, le retard 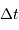 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 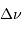 . Montrer que l'on a :
. Montrer que l'on a :
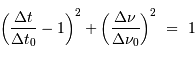
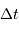 et
et 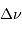 se réduit, pour les mesures effectuées, à
se réduit, pour les mesures effectuées, à 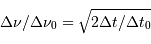 Comment interpréter les variations temporelles d'intensité du signal ?
Comment interpréter les variations temporelles d'intensité du signal ?
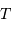 , la période de rotation propre de Mercure.
, la période de rotation propre de Mercure.
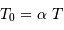 . Quelle signification donner à
. Quelle signification donner à 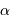 ?
De quelle fraction simple
?
De quelle fraction simple 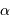 est-il proche ? Est-ce un hasard ?
est-il proche ? Est-ce un hasard ?
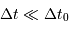 , et en tirer les conséquences.
, et en tirer les conséquences.
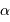 avec l'appliquette, la relation entre
avec l'appliquette, la relation entre 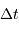 et
et 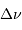 se traduit par :
se traduit par :
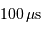 ; on se contentera également d'un ordre de grandeur grossier]
; on se contentera également d'un ordre de grandeur grossier]
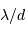 .
.

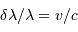 (à faible vitesse) est tellement prégnante que l'on peut très bien, en l'appliquant, définir une
(à faible vitesse) est tellement prégnante que l'on peut très bien, en l'appliquant, définir une 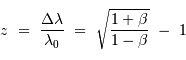
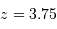 et
et 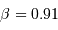 .
.
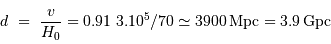
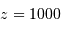
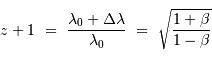
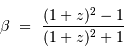
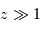 , le développement limité conduit à :
, le développement limité conduit à :
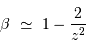
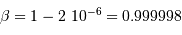 , ce qui est très rapide !
, ce qui est très rapide !
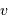 telle que :
telle que :
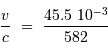
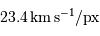 .
.
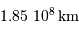 , soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
, soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
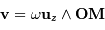
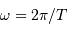 la rotation angulaire.
la rotation angulaire.
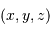 (avec bien sûr
(avec bien sûr 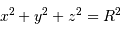 :
:
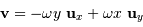
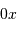 , càd
, càd 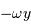
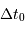 de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
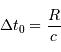
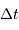 sur la carte
de Mercure [
sur la carte
de Mercure [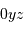 ] sont des lignes à coordonnée
] sont des lignes à coordonnée 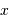 fixée. Analytiquement, à la surface de la planète et dans le plan du ciel
fixée. Analytiquement, à la surface de la planète et dans le plan du ciel 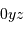 , l'équation
, l'équation
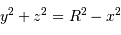

 Pour un point de Mercure de coordonnées
Pour un point de Mercure de coordonnées
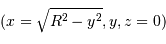 , le retard
, le retard 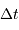 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 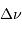 vérifient :
vérifient :
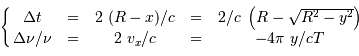
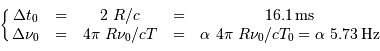
 .
On en déduit, pour un point du plan équatorial (
.
On en déduit, pour un point du plan équatorial (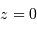 ) :
) :
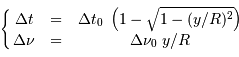
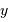 , il sort la relation demandée :
, il sort la relation demandée :
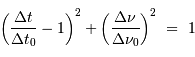
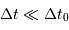 . Il s'ensuit que la relation entre
. Il s'ensuit que la relation entre 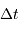 et
et 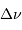 se simplifie en
se simplifie en
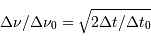
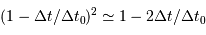 . Il en sort l'estimation de
. Il en sort l'estimation de 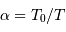 :
:
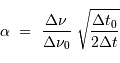
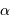 de l'ordre de 1.65, voisin de 5/3.
de l'ordre de 1.65, voisin de 5/3. 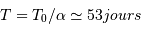 .
.
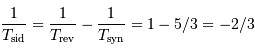
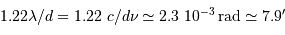 . En regard, Mercure intercepte une fraction angulaire
. En regard, Mercure intercepte une fraction angulaire 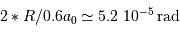 . La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit
. La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit 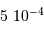 .
.