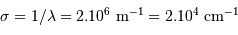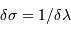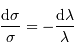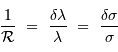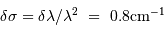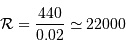Analyser spectralement la lumière est à la base de l'astrophysique. Cette section a pour but de rappeler quelques principes de physique permettant une analyse spectrale efficace. L'instrumentation nécessaire s'appuie sur le réseau de diffraction, bien plus efficace pour disperser la lumière qu'un prisme. Mais la mise en oeuvre du réseau nécessite un environnement précis.
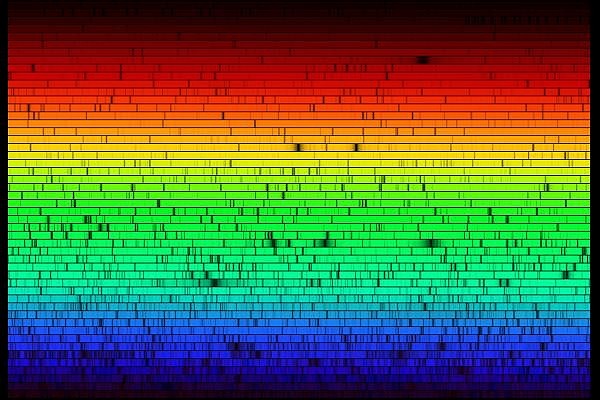
Le spectre solaire à haute résolution spectrale, obtenu avec un spectromètre échelle. Les couleurs comme l'aspect du spectre résultent d'un traitement d'image complexe.
Crédit :
NOAO
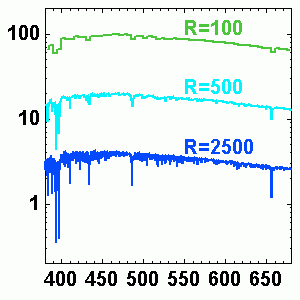
Spectre stellaire visible théorique à diverses résolutions spectrales
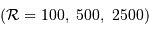
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
Crédit :
ASM
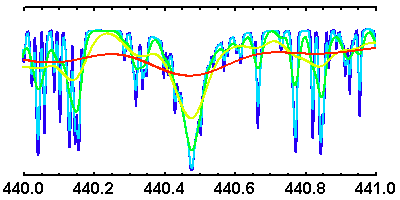
Échantillon d'un spectre stellaire observé à diverses résolutions spectrales
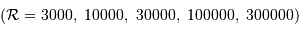
, avec renormalisation du flux.
Crédit :
ASM
Résolution spectrale
Plus la résolution d'un spectre stellaire théorique est élevée :
 Objectifs
Objectifs
Définir les notions de résolution spectrale : élément de résolution ; pouvoir de résolution ; intervalle spectral élémentaire.
Le pouvoir de résolution
Le pouvoir de résolution spectrale mesure la capacité à distinguer deux longueurs d'onde différentes 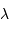 et
et 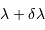 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
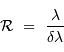
Le pouvoir de résolution est d'autant plus élevé que l'élément de résolution 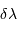 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
Conversions
Le pouvoir de résolution peut être exprimé avec les diverses grandeurs spectrales (longueur d'onde 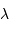 , fréquence
, fréquence 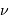 ) :
) :
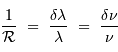
Il peut également être traduit en une vitesse, via l'équivalent Doppler:
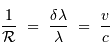
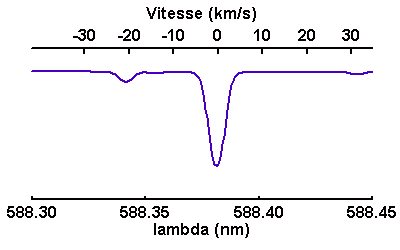
Raie stellaire représentée en fonction de la longueur d'onde ou de la vitesse repérée par rapport au centre de la raie.
Crédit :
ASM
Diverses résolutions
| Instrument | Pouvoir de résolution typique | 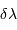 @ 500 nm (nm) @ 500 nm (nm) | vitesse (km/s) |
| Prisme | 500 | 1 | 600 |
| Réseau | 5000 | 0.1 | 60 |
| Réseau blazé | 50000 | 0.01 | 6 |
Le doublet du sodium
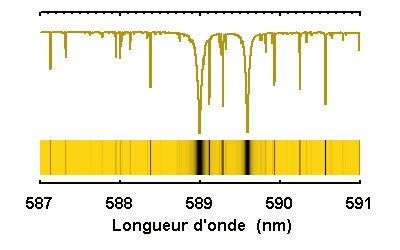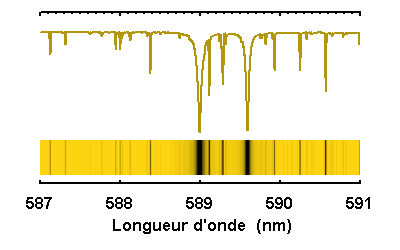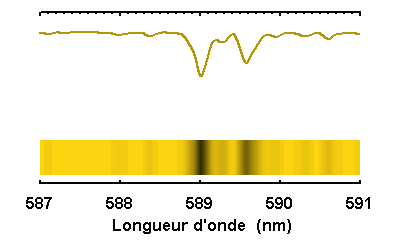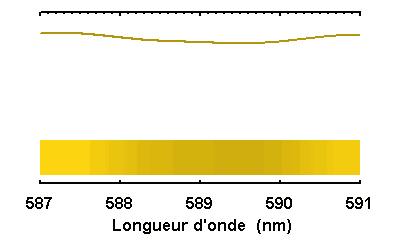
Le doublet jaune du sodium du spectre solaire,
simulé à diverses résolutions spectrales.
Crédit :
ASM
Résolution variable
Selon la résolution spectrale, des raies bien marquées, comme celles du sodium à 589.0 et 589.6 nm, apparaîtront plus ou moins clairement, avec l'identification de raies fines entre les 2 éléments du doublet, ou bien noyées dans le flux continu.
 Résolution et variable spectrale
Résolution et variable spectrale
Difficulté : ☆
Temps : 10 min
Un spectromètre assure un pouvoir de résolution 25 000 dans le visible à 500 nm.
Question 1)
Déterminer la largeur d'un élément spectral élémentaire.
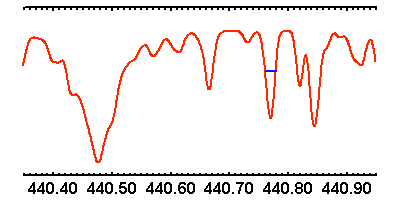
 Quelle résolution ?
Quelle résolution ?
Difficulté : ☆
Temps : 20 min
Le spectre ci-joint (voir l'appliquette) a été enregistré aux
alentours de 440.5 nm. Il s'agit d'estimer sa résolution, en fait
limitée par la résolution instrumentale.

Question 1)
Vaut-il mieux effectuer la mesure sur une raie fine ou une raie large ?
Réfléchir aux causes d'élargissement de la raie.
Question 2)
Estimer alors la résolution instrumentale
Estimer la largeur d'une raie à mi-hauteur
 Prérequis
Prérequis
Même s'il reprend les bases théoriques, ce cours suppose que le réseau a déjà été étudié en physique. Un réseau est alimenté en faisceau parallèle par une fente source, et en donne une série d'images colorées.
 Objectifs
Objectifs
Caractériser les interférences constructives d'un réseau ; voir la distribution de l'énergie dans la figure d'interférence.
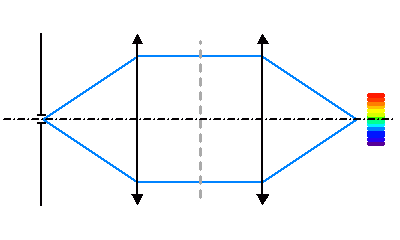
Le réseau donne une série d'images colorées de la fente source.
Crédit :
ASM
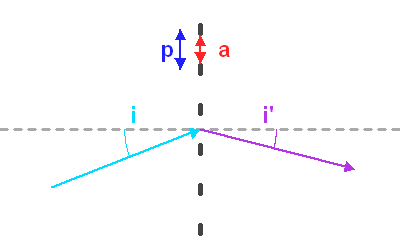
Paramètres du réseau, et définition des angles des faisceaux incident et diffracté.
Crédit :
ASM
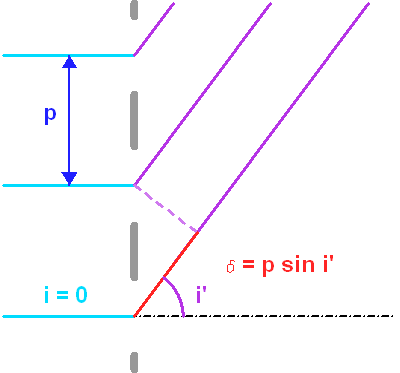
À incidence nulle, la différence de marche entre 2 rayons consécutifs, vaut
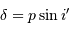
. Elle correspond au déphasage
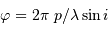
.
Crédit :
ASM
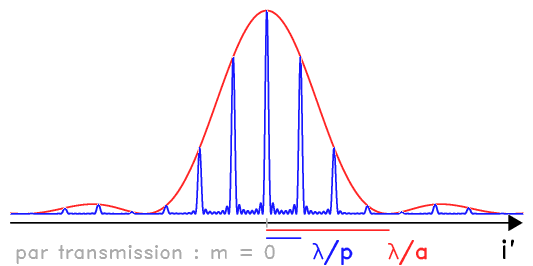
Les interférences se construisent principalement dans le lobe principal de la tache de diffraction d'une fente du réseau (en rouge).
Crédit :
ASM
Le rôle de la diffraction puis des interférences
La diffraction par une fente du réseau détermine les différentes directions vers lesquelles la lumière est envoyée, chacun des fentes du réseau se comportant comme une source secondaire.
Les interférences entre ces différentes sources secondaires construisent les franges d'interférences, d'autant plus fines que le réseau comporte un nombre important de traits (cf. calcul de l'intensité de la figure d'interférence).
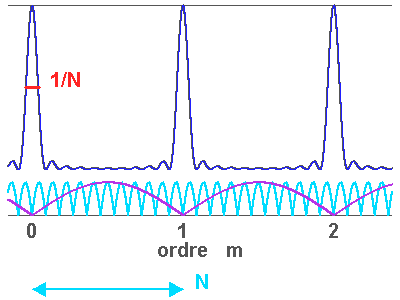
Représentation des numérateur (bleu ciel) et dénominateur (violet) de l'intensité diffractée par le réseau (en bleu). Les pics d'interférence apparaissent pour chaque annulation du terme
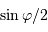
du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits
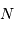
.
Crédit :
ASM
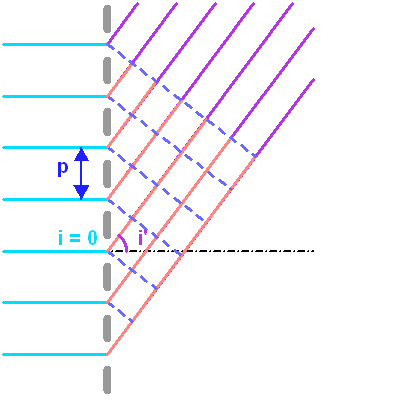
Sommation des différentes amplitudes.
Crédit :
ASM
Intensité de la figure d'interférence
L'intensité de la figure d'interférence est issue du double effet de la
diffraction par une seule fente et des interférences par 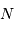 fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note
fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note 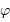 le déphasage entre 2 fentes consécutives, et
le déphasage entre 2 fentes consécutives, et 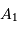 l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
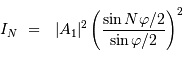
 Démonstration
Démonstration
La sommation des amplitudes conduit à :
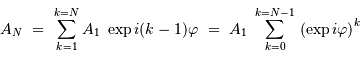
Le traitement de la somme des termes d'une suite en progression géométrique
donne :
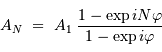
On calcule l'intensité en factorisant le numérateur et le dénominateur
par l'exponentielle complexe de l'angle moitié (de module unité), pour
aboutir à :
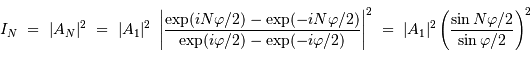
Le terme d'intensité est important uniquement lorsque le dénominateur s'annule. Dans ce cas, le numérateur s'annule également et, par continuité du rapport,
le pic d'intensité tend vers 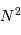 . Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille
. Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille 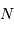 fois plus rapidement que le dénominateur ; elle est donc
fois plus rapidement que le dénominateur ; elle est donc 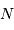 fois inférieure à la largeur entre 2 ordres consécutifs.
fois inférieure à la largeur entre 2 ordres consécutifs.
Inefficacité du réseau par transmission
L'inconvénient du réseau par transmission ici décrit est qu'il n'est a priori pas efficace : l'essentiel de l'énergie passe dans l'ordre 0, inintéressant pour la dispersion. Un concept technologique spécifique pare cet inconvénient : le réseau blazé.
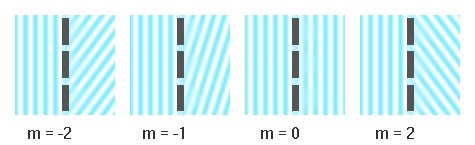
Variation de l'angle de dispersion en fonction de l'ordre d'interférence.
Crédit :
ASM
Dispersion du réseau / ordre d'interférence
La déviation des ordres diffractés par le réseau dépend de l'ordre d'interférence.

Variation de l'angle de dispersion en fonction de la couleur de l'onde plane monochromatique incidente.
Crédit :
ASM
Dispersion du réseau / couleur
La déviation des ordres diffractés par le réseau dépend de la longueur d'onde de l'onde plane
incidente.
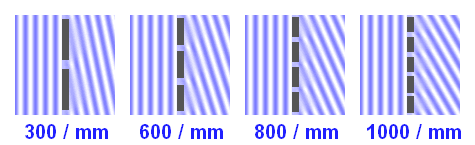
Variation de l'angle de dispersion en fonction du nombre de traits du réseau, donné en traits par millimètre, l'ordre (ici m = 1) et la longueur d'onde étant fixés.
Crédit :
ASM
 Prérequis
Prérequis
Etude du réseau en physique.
 Objectifs
Objectifs
Caractériser la dispersion d'un réseau, càd sa capacité à distinguer les différentes couleurs.
Relation du réseau
Rappel : la condition d'interférences constructives s'écrit :
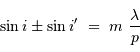
avec 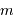 l'ordre d'interférence (entier),
l'ordre d'interférence (entier), 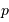 le pas du réseau,
le pas du réseau, 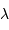 la longueur d'onde d'étude.
la longueur d'onde d'étude.
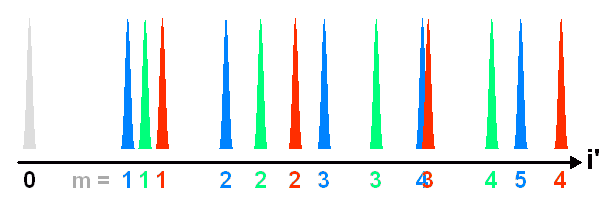
Les ordres d'interférences des différentes couleurs progressent d'autant plus vite que la longueur d'onde est petite. Très rapidement, les différents ordres des différentes couleurs se mêlent.
Crédit :
ASM
Ordres d'interférences
A couleur fixée, mais ordre d'interférence 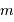 variable, la différentiation de la relation constitutive du réseau s'écrit :
variable, la différentiation de la relation constitutive du réseau s'écrit :
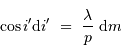
Un pas d'interférence, correspondant à 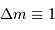 , correspond à un
intervalle angulaire :
, correspond à un
intervalle angulaire :
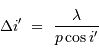
Ce pas varie directement avec la couleur de l'onde considérée.
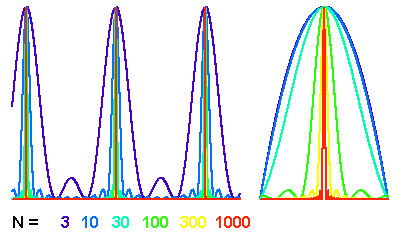
Diffraction et interférences à
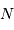
ondes
![(N = [3, 10, 30, 100, 300, 1000])](../pages_interference/equations_reseau-dispersion/equation20.png)
. La largeur de la tache principale varie comme
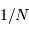
. La figure de droite
zoome sur un ordre donné.
Crédit :
ASM
Le pouvoir de résolution théorique
Le nombre 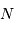 de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire
de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire 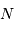 fois moindre qu'un ordre :
fois moindre qu'un ordre :
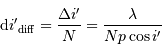
Le pouvoir de résolution théorique du réseau s'écrit, s'il est limité par la seule diffraction, en application de ce qui précède 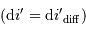 :
:
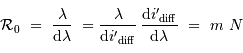
Le pouvoir de résolution théorique augmente avec le nombre de traits éclairés et avec l'ordre d'interférence.
AN : avec un réseau blazé de 100 mm, 100 traits/mm et travaillant à l'ordre 40, le pouvoir de résolution théorique atteint 400 000.
Inefficacité du réseau par transmission
L'inconvénient du réseau par transmission ici décrit est qu'il n'est toujours pas efficace : la dispersion spectrale est d'autant plus grande que l'ordre du réseau est élevé, mais l'essentiel de l'énergie reste dans l'ordre 0, inintéressant pour la dispersion. De plus, la superposition des ordres mélange les couleurs.

Lumière rouge, ordre 1
Crédit :
ASM

Lumière verte, ordre 1
Crédit :
ASM

Lumière bleue, ordre 1
Crédit :
ASM

Lumière verte, ordre 2
Crédit :
ASM

Lumière verte, ordre -1
Crédit :
ASM

Lumière verte, ordre 1, grand pas
Crédit :
ASM

Lumière verte, ordre 1, petit pas
Crédit :
ASM
La déviation du réseau
Les animations montrent la création des ordres d'interférence par interférences constructives, pour différents ordres et couleurs.
Attention : ces animations supposent indûment valide à courte distance l'approximation de Fraunhofer, qui décrit la diffraction uniquement à grande distance de l'objet diffractant.
Voir comme la déviation varie avec :
- l'ordre d'interférence : cf animations pour différents ordres,
1,
2 ,
-1
- la longueur d'onde : cf animations pour différentes couleurs,
rouge,
vert,
bleu
- le pas du réseau : cf animations pour différents pas,
grand, ou
petit

Le double réseau de l'instrument HARPS (ESO, télescope de 3.6 m). Les 2 réseaux côte à côte couvrent une surface de
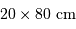
.
Crédit :
HARPS/ESO
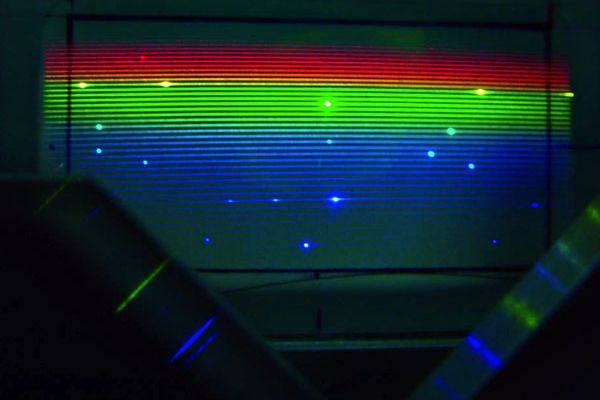
Image projetée sur un écran translucide d'un spectre-échelle
obtenu avec un spectromètre (SOPHIE, OHP) incluant un réseau blazé
et un post-disperseur.
Crédit :
OHP/CNRS
Un réseau efficace
Un réseau-échelle ou réseau blazé (a blaze of color =
resplendissant de couleur) traite efficacement la dispersion : il envoie la puissance lumineuse incidente dans des ordres élevés du spectre, avec une grande dispersion spectrale. Il s'agit d'un réseau par réflexion, très couramment utilisé en instrumentation astrophysique.

Image d'un
spectre-échelle à haute résolution spectrale obtenu avec une caméra CCD. Le spectre de l'étoile apparaît ici sous l'aspect de bandes sombres. L'étalonnage en longueur d'onde est apporté par les raies en émission d'une lampe spectrale (Thorium Argon), dont le spectre est intercalé avec celui de l'étoile, et enregistré simultanément.
Crédit :
ESO/ASM
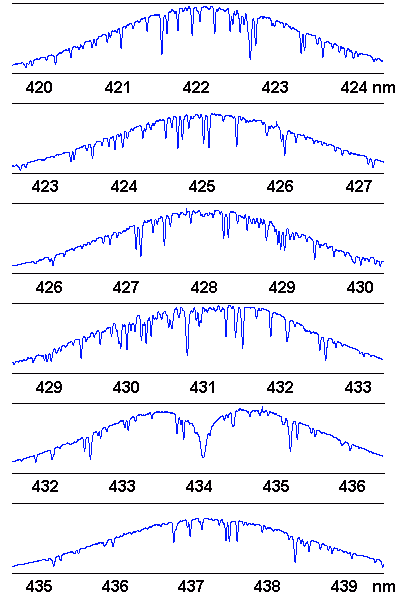
Aperçu de 6 ordres du spectre obtenu avec le spectromètre Harps. La diffraction par chaque trait du réseau est responsable du profil d'étalement du flux ; la séparation des ordres est obtenue grâce à un deuxième élément dispersif, dans une direction perpendiculaire à celle du premier réseau.
Crédit :
ESO/ASM

La dispersion croisée du spectromètre Harps est assurée par un
grisme, qui correspond à un réseau par transmission gravé sur un
prisme.
Crédit :
ESO
Les ordres d'un réseau blazé
Une deuxième dispersion, dite
dispersion croisée, des ordres diffractés par un
réseau blazé permet d'obtenir un spectre sur un large intervalle
spectral divisé en plusieurs
ordres.
L'intensité dans chaque
ordre est modulée par la fonction d'Airy de la fente d'entrée.
 Objectifs
Objectifs
Introduire les propriétés du réseau blazé, dont l'intérêt est d'envoyer l'énergie diffractée dans un ordre d'interférence non nul.
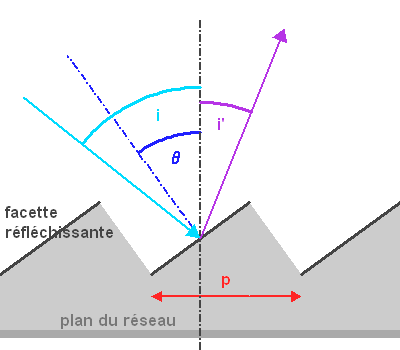
Profil d'un réseau blazé ou réseau échelle, et définition des angles. Les facettes réfléchissantes du réseau sont gravées avec une inclinaison
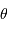
par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
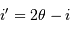
. Les angles

et
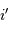
restent définis par rapport au plan du réseau.
Crédit :
ASM
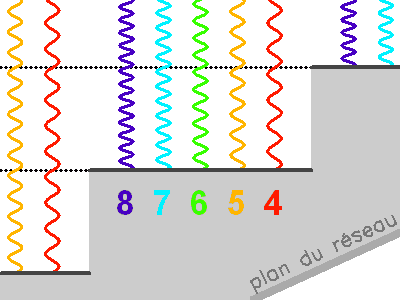
Le maximum d'énergie renvoyée (dans la direction de l'optique géométrique) correspond à un ordre non nul, d'autant plus grand que la longueur d'onde est petite. Dans la pratique, l'inclinaison du faisceau est le plus souvent très proche de la normale aux facettes.
Crédit :
ASM
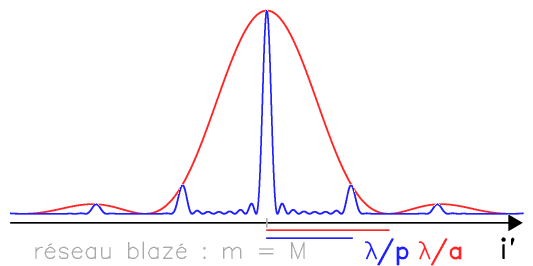
Pour un réseau blazé, les interférences se construisent principalement dans le lobe principal de la tache de diffraction, centré sur une frange d'ordre non nul.
Crédit :
ASM
Le réseau blazé
Le réseau par transmission n'est pas efficace. La diffraction envoie essentiellement l'énergie dans l'ordre 0, qui n'est pas dispersif, ce qui n'est guère intéressant.
L'intérêt du réseau blazé est d'envoyer le flux dans un ordre d'interférence non nul dans les conditions de l'optique géométrique (les conditions usuelles d'utilisation sont proches du cas 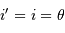 , où
, où 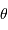 est l'angle de blaze). Cet ordre dépend de la couleur étudié.
est l'angle de blaze). Cet ordre dépend de la couleur étudié.
D'un point de vue énergétique, le montage optique d'un réseau blazé s'arrange pour voir essentiellement la tache de diffraction du réseau (déterminée par une facette élémentaire).
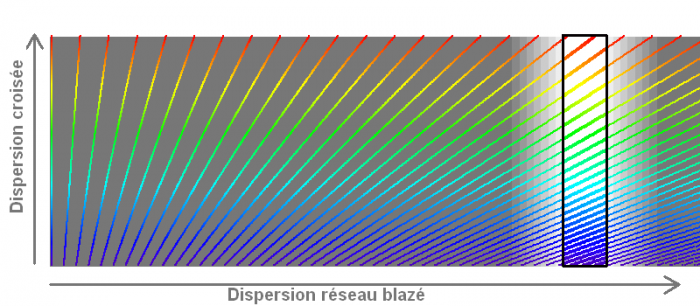
Avec un réseau blazé, l'image diffractée de la fente d'entrée correspond à un ordre d'interférences non nul. Cet ordre d'interférence varie d'une couleur à l'autre. Une dispersion à basse résolution spectrale, perpendiculaire à la haute résolution apportée par le réseau blazé, permet de séparer ces ordres et d'obtenir une image d'un large intervalle spectral constitué d'une succession d'ordres.
Crédit :
ASM
Nécessité d'une dispersion croisée
Par rapport au réseau par transmission, le réseau blazé permet un
travail dans un ordre d'interférence élevé, assurant un pouvoir de
résolution théorique élevé. Mais, à lui seul, le réseau blazé
n'assure pas une dispersion optimale : les ordres restent
superposés, aboutissant à la confusion des couleurs si chèrement
dispersées. Il faut adjoindre au
réseau blazé un deuxième
élément dispersif, assurant une dispersion dans une direction
perpendiculaire, qui permet de distinguer les différents ordres.
Avec 2 dispersions à angle droit, la source doit nécessairement
être ponctuelle (en pratique, souvent une fibre).
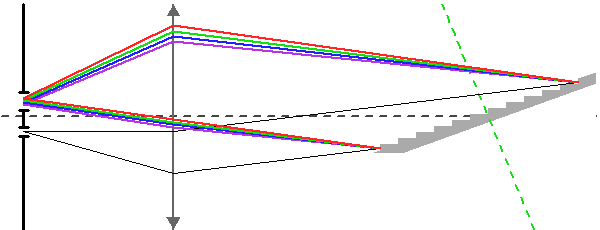
Montage de Littrow avec réseau blazé. Le plan du réseau est incliné par rapport à l'axe optique de telle sorte que les facettes du réseau sont quasi perpendiculaires à l'axe optique.
Crédit :
ASM

Le réseau donne une série d'images colorées de la fente source.
Crédit :
ASM
Montage de principe
Le réseau est alimenté en faisceau parallèle par une fente source ou un trou source. Le
montage de principe est donc simplement un montage conjuguant la source à son image en passant via 2 lentilles équivalentes par un faisceau parallèle. Le réseau donne en fait une série d'images colorées de la
fente source.
Spectromètre et réseau
En pratique, c'est évidemment plus complexe.
L'insertion du réseau dans le spectromètre nécessite :
- Une fente d'entrée, ou tout dispositif réduisant le champ (un trou source dans le cas du réseau blazé).
- Une bonne illumination de la fente ou du trou source.
- Une optique assurant un bon éclairement du réseau.
L'appliquette ci-joint permet de lire le schéma optique de l'instrument CRIRES
(CRyogenic high-resolution IR Echelle Spectrometer) du VLT.

Montage de Littrow
Un montage optique couramment utilisé avec un réseau blazé est celui de type Littrow, où une optique unique alimente le réseau en lumière parallèle et collecte le faisceau dispersé. Les facettes du réseau blazé sont éclairées sous une incidence quasi-nulle (mais correspondant à une incidence élevée par rapport au plan du réseau).
 Prérequis
Prérequis
Etude du réseau en physique.
 Objectifs
Objectifs
Lier le pouvoir de résolution spectrale d'un instrument disperseur avec réseau aux conditions de formation d'image.
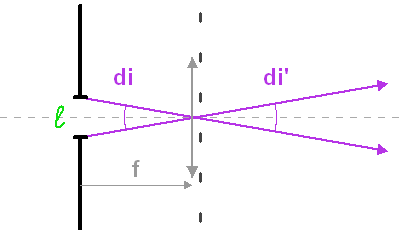
Fente du réseau et collimation.
Crédit :
ASM
La taille de la fente d'entrée
Le rôle de l'optique géométrique ne doit pas être oublié : il peut dimensionner la résolution effective du réseau. Avec 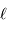 la largeur de la fente et
la largeur de la fente et 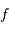 la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
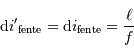
Le pouvoir de résolution limité par la largeur de la fente d'entrée 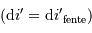 s'écrit :
s'écrit :
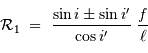
où subsistent les conditions géométriques de l'éclairement du réseau. Dans les conditions d'un réseau blazé éclairé quasi normalement aux facettes, 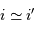 et avec le signe + correspondant au réseau par réflexion :
et avec le signe + correspondant au réseau par réflexion :
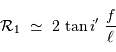
Un pouvoir de résolution optimal nécessite une source de petite taille et une grande focale. Avec une focale de l'ordre du mètre, une fente de 100 micromètres (en fait une fibre), et 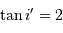 , le pouvoir de résolution géométrique vaut 40 000.
, le pouvoir de résolution géométrique vaut 40 000.
La finesse de la fente d'entrée assure la finesse des images monochromatiques ; mais fermer la fente est réalisé au détriment de la luminosité. Assurer une longue focale nécessite un grand réseau, ce qui a un coût.
 Le réseau du spectromètre HARPS
Le réseau du spectromètre HARPS
Difficulté : ☆☆
Temps : 20 min
Question 1)
Le montage du spectromètre HARPS assure un pouvoir de résolution
de l'ordre de 120 000. La focale de l'optique de chambre valant
1.56 m, en déduire la taille de la fente d'entrée, sachant que par
ailleurs l'illumination du réseau a lieu dans les conditions 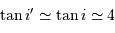 .
.
[1 points]
Question 2)
Le flux collecté par le télescope a un diamètre de 3.6 m, qui devient dans l'instrument 20 cm. En déduire le grossissement.
[1 points]
Question 3)
Déduire de ce qui précède l'ordre de grandeur du champ de vue sur le ciel.
[2 points]


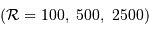 . La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.

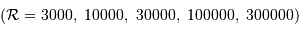 , avec renormalisation du flux.
, avec renormalisation du flux.
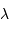 et
et 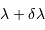 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
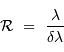
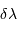 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
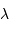 , fréquence
, fréquence 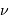 ) :
) :
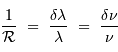
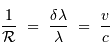

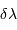 @ 500 nm (nm)
@ 500 nm (nm) 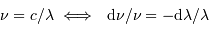 .
.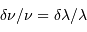 .
.
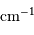 . Exprimer le nombre d'onde
. Exprimer le nombre d'onde 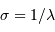 et la résolution
et la résolution 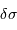 dans ce système d'unité.
dans ce système d'unité.
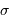 , c'est simple. Pour
, c'est simple. Pour 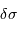 , il faut revenir à la définition.
, il faut revenir à la définition.
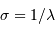 , calculer la différentielle
, calculer la différentielle 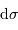 .
.




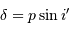 . Elle correspond au déphasage
. Elle correspond au déphasage 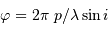 .
.
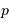 la
la 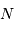 le nombre de traits,
le nombre de traits, 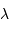 la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
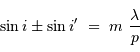
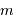 , entier, l'ordre d'interférence. Le signe
, entier, l'ordre d'interférence. Le signe 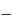 dans cette relation concerne un réseau par transmission, le signe
dans cette relation concerne un réseau par transmission, le signe  un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du
un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du 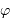 entre les amplitudes complexes issues de 2 traits consécutifs, vaut
entre les amplitudes complexes issues de 2 traits consécutifs, vaut 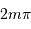 (ou bien, de façon équivalente, que la différence de marche vaut
(ou bien, de façon équivalente, que la différence de marche vaut 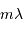 ).
).


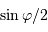 du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits
du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits 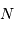 .
.

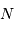 fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note
fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note 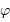 le déphasage entre 2 fentes consécutives, et
le déphasage entre 2 fentes consécutives, et 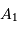 l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
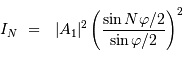
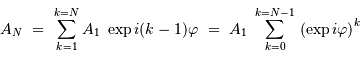
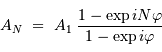
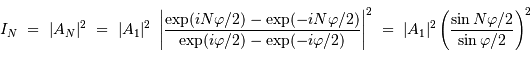
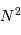 . Chaque
. Chaque 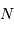 fois plus rapidement que le dénominateur ; elle est donc
fois plus rapidement que le dénominateur ; elle est donc 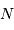 fois inférieure à la largeur entre 2 ordres consécutifs.
fois inférieure à la largeur entre 2 ordres consécutifs.



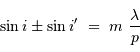
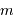 l'ordre d'interférence (entier),
l'ordre d'interférence (entier), 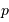 le pas du réseau,
le pas du réseau, 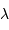 la longueur d'onde d'étude.
la longueur d'onde d'étude.
 fixée, les variations de
l'angle de sortie
fixée, les variations de
l'angle de sortie 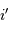 avec
avec 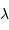 . Elle est obtenue par différentiation de la relation du réseau :
. Elle est obtenue par différentiation de la relation du réseau :
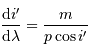
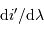 croît avec l'ordre
croît avec l'ordre 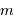 et la fréquence spatiale du réseau
et la fréquence spatiale du réseau 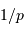 .
La résolution
.
La résolution 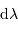 dépend des paramètres du réseau, mais aussi de la précision
dépend des paramètres du réseau, mais aussi de la précision 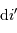 avec laquelle on peut déterminer l'angle
avec laquelle on peut déterminer l'angle 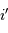 .
.

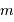 variable, la différentiation de la
variable, la différentiation de la 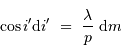
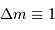 , correspond à un
intervalle angulaire :
, correspond à un
intervalle angulaire :
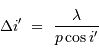

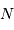 ondes
ondes ![(N = [3, 10, 30, 100, 300, 1000])](../pages_interference/equations_reseau-dispersion/equation20.png) . La largeur de la tache principale varie comme
. La largeur de la tache principale varie comme 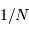 . La figure de droite
zoome sur un ordre donné.
. La figure de droite
zoome sur un ordre donné.
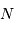 de traits du réseau
de traits du réseau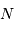 fois moindre qu'un ordre :
fois moindre qu'un ordre :
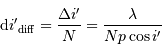
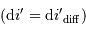 :
:
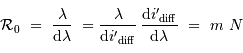







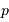 et la largeur de fente
et la largeur de fente 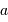 sont très proches pourra travailler efficacement dans combien d'ordres :
sont très proches pourra travailler efficacement dans combien d'ordres :

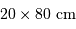 .
.





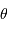 par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
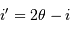 . Les angles
. Les angles  et
et 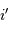 restent définis par rapport au plan du réseau.
restent définis par rapport au plan du réseau.


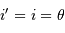 , où
, où 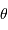 est l'angle de blaze). Cet ordre dépend de la couleur étudié.
est l'angle de blaze). Cet ordre dépend de la couleur étudié.

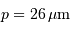 et d'angle
et d'angle 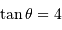 observe dans le rouge (600 nm) dans l'ordre
observe dans le rouge (600 nm) dans l'ordre


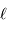 la largeur de la fente et
la largeur de la fente et 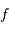 la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
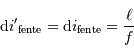
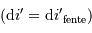 s'écrit :
s'écrit :
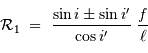
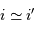 et avec le signe + correspondant au réseau par réflexion :
et avec le signe + correspondant au réseau par réflexion :
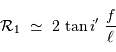
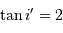 , le pouvoir de résolution géométrique vaut 40 000.
, le pouvoir de résolution géométrique vaut 40 000.
![{\cal R} \ = \mathrm{min}\ [ {\cal R}_0, \ {\cal R}_1]](../pages_interference/equations_spectro-reseau/equation9.png)
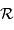 du réseau, inférieur au pouvoir de résolution théorique, dépend :
du réseau, inférieur au pouvoir de résolution théorique, dépend :
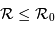 , qui varie comme
, qui varie comme 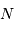
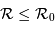 , qui varie comme
, qui varie comme 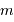
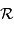 varie comme
varie comme 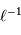
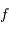 de l'optique et la largeur
de l'optique et la largeur 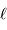 de la fente d'entrée comme
de la fente d'entrée comme
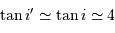 .
.
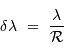
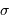 donne :
donne :