
|
Etude du réseau en physique.
Caractériser la dispersion d'un réseau, càd sa capacité à distinguer les différentes couleurs.
Rappel : la condition d'interférences constructives s'écrit :
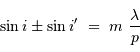
avec 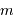 l'ordre d'interférence (entier),
l'ordre d'interférence (entier), 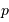 le pas du réseau,
le pas du réseau, 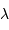 la longueur d'onde d'étude.
la longueur d'onde d'étude.
La dispersion angulaire relie, à incidence  fixée, les variations de
l'angle de sortie
fixée, les variations de
l'angle de sortie 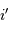 avec
avec 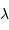 . Elle est obtenue par différentiation de la relation du réseau :
. Elle est obtenue par différentiation de la relation du réseau :
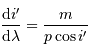
La dispersion 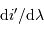 croît avec l'ordre
croît avec l'ordre 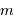 et la fréquence spatiale du réseau
et la fréquence spatiale du réseau 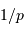 .
La résolution
.
La résolution 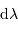 dépend des paramètres du réseau, mais aussi de la précision
dépend des paramètres du réseau, mais aussi de la précision 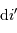 avec laquelle on peut déterminer l'angle
avec laquelle on peut déterminer l'angle 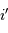 .
.
A couleur fixée, mais ordre d'interférence 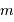 variable, la différentiation de la relation constitutive du réseau s'écrit :
variable, la différentiation de la relation constitutive du réseau s'écrit :
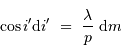
Un pas d'interférence, correspondant à 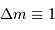 , correspond à un
intervalle angulaire :
, correspond à un
intervalle angulaire :
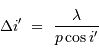
Ce pas varie directement avec la couleur de l'onde considérée.
Le nombre 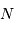 de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire
de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire 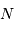 fois moindre qu'un ordre :
fois moindre qu'un ordre :
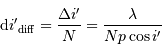
Le pouvoir de résolution théorique du réseau s'écrit, s'il est limité par la seule diffraction, en application de ce qui précède 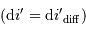 :
:
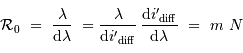
Le pouvoir de résolution théorique augmente avec le nombre de traits éclairés et avec l'ordre d'interférence.
AN : avec un réseau blazé de 100 mm, 100 traits/mm et travaillant à l'ordre 40, le pouvoir de résolution théorique atteint 400 000.
L'inconvénient du réseau par transmission ici décrit est qu'il n'est toujours pas efficace : la dispersion spectrale est d'autant plus grande que l'ordre du réseau est élevé, mais l'essentiel de l'énergie reste dans l'ordre 0, inintéressant pour la dispersion. De plus, la superposition des ordres mélange les couleurs.