
|
Etude du réseau en physique.
Lier le pouvoir de résolution spectrale d'un instrument disperseur avec réseau aux conditions de formation d'image.
Le rôle de l'optique géométrique ne doit pas être oublié : il peut dimensionner la résolution effective du réseau. Avec 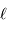 la largeur de la fente et
la largeur de la fente et 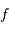 la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
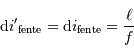
Le pouvoir de résolution limité par la largeur de la fente d'entrée 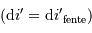 s'écrit :
s'écrit :
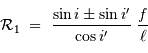
où subsistent les conditions géométriques de l'éclairement du réseau. Dans les conditions d'un réseau blazé éclairé quasi normalement aux facettes, 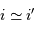 et avec le signe + correspondant au réseau par réflexion :
et avec le signe + correspondant au réseau par réflexion :
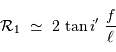
Un pouvoir de résolution optimal nécessite une source de petite taille et une grande focale. Avec une focale de l'ordre du mètre, une fente de 100 micromètres (en fait une fibre), et 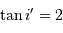 , le pouvoir de résolution géométrique vaut 40 000.
, le pouvoir de résolution géométrique vaut 40 000.
La finesse de la fente d'entrée assure la finesse des images monochromatiques ; mais fermer la fente est réalisé au détriment de la luminosité. Assurer une longue focale nécessite un grand réseau, ce qui a un coût.
Le pouvoir de résolution réel est conditionné par la plus petite valeur du pouvoir théorique ou limité par l'image géométrique de la fente d'entrée :
![{\cal R} \ = \mathrm{min}\ [ {\cal R}_0, \ {\cal R}_1]](../pages_interference/equations_spectro-reseau/equation9.png)
Un instrument bien dimensionné est conçu de façon à accorder la taille de la fente et la résolution optimale définie par la diffraction.
Des informations sur le réseau, on conclut que le pouvoir de résolution 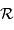 du réseau, inférieur au pouvoir de résolution théorique, dépend :
du réseau, inférieur au pouvoir de résolution théorique, dépend :
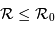 , qui varie comme
, qui varie comme 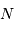
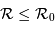 , qui varie comme
, qui varie comme 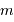
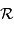 varie comme
varie comme 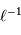
Un pouvoir de résolution élevé nécessite une fente d'entrée très étroite.