Exercice

Evolution du nuage proto-solaire

Dans cet exercice, nous allons essayer de comprendre pourquoi le nuage proto-solaire s'est aplati au cours de son évolution et pourquoi il s'est mis à tourner.

Question 1)

Dans le cas où les forces sont conservatives (pas de perte d'énergie sous forme de chaleur), comme c'est le cas pour la gravitation, pour tout objet en rotation, il y a conservation d'une grandeur que l'on appelle «moment cinétique» L (ou moment angulaire). Son expression est :

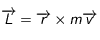
$\overrightarrow{L} = \overrightarrow{r} \times m\overrightarrow{v}$

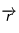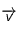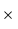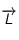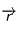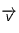où $\overrightarrow{r}$ est le rayon vecteur entre l'axe de rotation et l'objet, et $\overrightarrow{v}$ la vitesse de rotation de l'objet. Ce sont des grandeurs vectorielles (donc orientées en sens et direction). Le produit vectoriel $\times$ signifie que $\overrightarrow{L}$ est perpendiculaire à la fois à $\overrightarrow{r}$ et à $\overrightarrow{v}$ . Pour connaître son orientation, faites l'expérience suivante :

Avec votre main gauche (laissons la droite pour écrire*), pointez votre pouce selon une direction qui sera 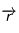$\overrightarrow{r}$ (disons de droite à gauche), votre majeur qui sera 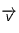$\overrightarrow{v}$ (perpendiculaire à 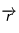$\overrightarrow{r}$ , vers vous pour simplifier le mouvement), votre index (tendu perpendiculairement aux deux autres doigts) pointera alors la direction de 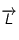$\overrightarrow{L}$ (axe de rotation de votre système). Quelle est cette direction ?

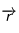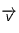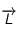(* si vous êtes gaucher, prenez votre main droite avec le majeur pour $\overrightarrow{r}$ , le pouce pour $\overrightarrow{v}$ ,votre index pointe vers $\overrightarrow{L}$ )

Question 2)

Revenons à notre nuage en rotation. On supposera 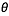theta , angle entre le rayon vecteur 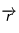$\overrightarrow{r}$ et le vecteur vitesse 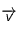$\overrightarrow{v}$ , égal à 90˚. Sachant que le rayon du nuage proto-solaire se réduit (à cause de la gravitation) au cours de son évolution, comment la vitesse évolue-t-elle au cours du temps ?

Aide

Orbites des planètes

Question 1)

Vous avez déjà rencontré une application du principe de conservation du moment cinétique dans votre cours sur les orbites des planètes. Savez-vous de quelle loi il s'agit ?