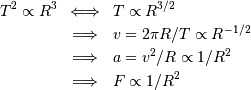Quel point de vue adopter ?
Comme le montrent les observations de Kepler, le mouvement de Mars, vu de la Terre et décrit dans un référentiel géocentrique, n'est pas des plus simples à comprendre. Ce qui ne va pas ? Le référentiel !
Mouvement de Mars vu de la Terre
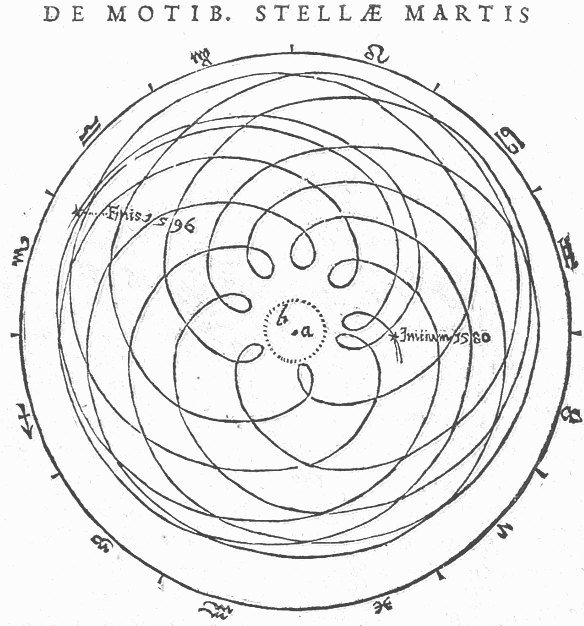
L'orbite de Mars vue dans le référentiel géocentrique. Schémas de Kepler de 1580 à 1596. La Terre est au centre, le soleil orbite sur le cercle en pointillés. Au cours de l'année martienne, la distance Terre-Mars peut varier dans des proportions de 1 à 6.
Crédit :
Bibliothèque de l'Observatoire de Paris
Mouvement de Mars vu de la Terre et du Soleil

L'orbite de Mars au voisinage de
l'
opposition planétaire, vue de la Terre ou dans le référentiel héliocentrique
Crédit :
ASM
Vue de la Terre, l'orbite apparente de Mars dessine une boucle.
Cette vision géocentrique complique la perception du phénomène. Vue du Soleil, à la conjonction planétaire, la Terre se contente de doubler Mars.
Problème : comment avoir, lorsque l'on est observateur terrestre, autre chose qu'une vision géocentrique ?
Point de vue héliocentrique
Les astronomes Copernic et Kepler ont résolu ce problème, en
conceptualisant ces mouvements, Copernic, en mettant le soleil au centre
du système solaire, Kepler en décrivant les mouvements planétaires par
ses 3 lois.
 Objectifs
Objectifs
La page "Des lois de Newton aux lois de
Kepler" montre comment l'on dérive aujourd'hui les lois de Kepler des lois de la gravitation et du formalisme de mécanique classique. Mais historiquement, les 3 lois de Kepler sont antérieures au formalisme newtonien, comme le plus souvent le fait observationnel précède la formalisation théorique. Il est important de voir comment les lois de Kepler portent en elles les germes de la loi de gravitation.
Ce qu'induit la première loi
La 1ère loi de Kepler donne
un rôle particulier
au soleil, qui peut être doublement interprété.
Du point de vue dynamique, le rôle central du soleil est clairement énoncé. Si
aujourd'hui la prépondérance du soleil au sein du système solaire
est un fait avéré et reconnu, il
n'en était rien au XVIIe siècle. Le Soleil est centre de force, et ce
d'autant plus que toute masse dans le système solaire est négligeable
devant la masse du soleil.
En terme de référentiel d'étude, la 1ère loi
introduit clairement le référentiel héliocentrique, qui est le "bon"
référentiel d'étude, car bien mieux galiléen que le référentiel
géocentrique. La première loi identifie donc clairement un centre de force supposé
immobile, ainsi que le bon référentiel associé.
Définition des coordonnées et vecteurs unitaires polaires
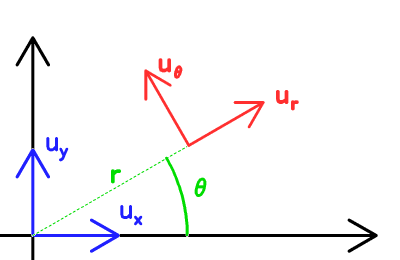
La base polaire plane est bien adaptée au problème képlérien : la 1ère
loi de Kepler énonce en effet que la trajectoire s'inscrit dans un plan,
et la 2ème loi que la force est centrale.
Crédit :
ASM
Ce qu'induit la deuxième loi
La 2ème loi de Kepler énonce la loi des aires,
càd la conservation du moment cinétique du système. Ceci est spécifique
des forces centrales. Des 1ère et 2ème lois ressort donc
l'idée que le soleil est centre de force. Cette force peut s'écrire
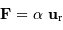 ,
le vecteur
,
le vecteur 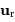 étant un vecteur
unitaire radial défini par
rapport au centre de force.
étant un vecteur
unitaire radial défini par
rapport au centre de force.
Ce qu'induit la troisième loi
Le lien entre la période et le
demi-grand axe donné
par la 3ème loi de Kepler est spécifique à une
dépendance particulière du module de la force vis à vis de la variable
radiale. Cette loi n'apparaît que pour une force variant en 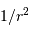 .
.
L'ensemble des lois de Kepler conduit finalement à une force s'écrivant de
la forme :
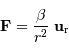
Les lois de Kepler n'en disent pas plus sur ce paramètre 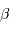 .
Ce sont les lois de la gravitation, dues à Isaac Newton, qui permettent d'expliciter sa forme.
.
Ce sont les lois de la gravitation, dues à Isaac Newton, qui permettent d'expliciter sa forme.
Des lois de Kepler à une force centrale variant comme l'inverse du carré de la distance
 Démonstration
Démonstration
En coordonnées polaires planes, définies dans le plan de l'orbite par rapport au foyer décrit par la 1ère loi de Kepler, on exprime les rayon vecteur, vitesse et accélération de l'objet par :
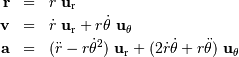
La composante orthoradiale de l'accélération s'identifie, à une constante près, à la dérivée temporelle du moment cinétique (perpendiculaire au plan de la trajectoire) :
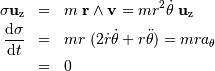
La nullité de la composante orthoradiale de l'accélération est bien la
signature d'une force centrale.
La démonstration de la 3ème loi de Kepler,
dans le cas d'un mouvement circulaire, dérive du jeu d'écriture suivant,
avec 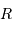 le rayon de l'orbite,
le rayon de l'orbite, 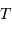 la période et
la période et 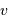 la vitesse de l'objet :
la vitesse de l'objet :
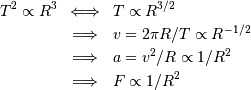



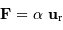 ,
le vecteur
,
le vecteur 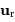 étant un
étant un 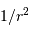 .
.
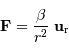
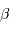 .
Ce sont les
.
Ce sont les 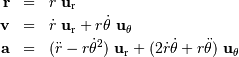
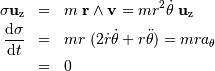
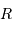 le rayon de l'orbite,
le rayon de l'orbite, 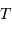 la période et
la période et 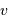 la vitesse de l'objet :
la vitesse de l'objet :