Un nouveau centre de force
En 1610, Galileo Galilei utilise, pour la première fois, une lunette pour l'observation du ciel. Il découvre un étrange ballet autour de Jupiter, qui évolue au fil des nuits. Cette découverte conforte les idées coperniciennes : il existe visiblement
d'autres centres de force que le Soleil ou la Terre.
Cahier d'observation

Comme le montrent les différents croquis établis au fil des nuits, l'environnement de Jupiter présente un décor changeant. Alors que le déplacement apparent de la planète par rapport aux étoiles entraîne un renouvellement permanent du "décor de fond", quatre objets (les principaux satellites de Jupiter, dit galiléens) évoluent autour de Jupiter.
Leurs périodes de révolution (de 1.7 j pour Io à 16 j pour Callisto) assurent une nouvelle configuration de nuit en nuit.
Crédit :
Bibliothèque de l'Observatoire de Paris
A deux c'est mieux !
L'approximation du système à 2 corps consiste à supposer le système isolé du reste de l'univers, càd à négliger toute autre interaction. Cette approximation est souvent vérifiée, au moins en première approximation, à ne nombreuse échelles.
Cette prégnance du système à 2 corps est ici illustrée à diverses
échelles :
Le système Terre-Lune

Le système Terre-Lune. La dynamique du système relève essentiellement du
problème à 2 corps, perturbé par le caractère non ponctuel des objets
(
effet de marée), et les
autres potentiels gravitationnels du système solaire.
Crédit :
NASA
Etoile double

Le couple Sirius A - Sirius B : Sirius A est une étoile de type A1V,
Sirius B une naine blanche. Leur séparation est de l'ordre de 20 AU,
pour une période orbitale de 50 ans.
L'image en X obtenue par le satellite Chandra (NASA) permet de visualiser les 2 composantes, qui dans le visible présentent un contraste de 10
magnitudes.
Crédit :
NASA
Etoile double
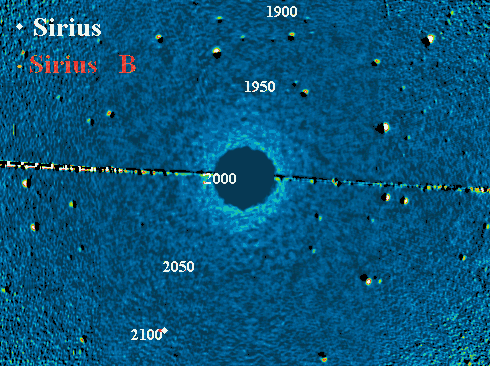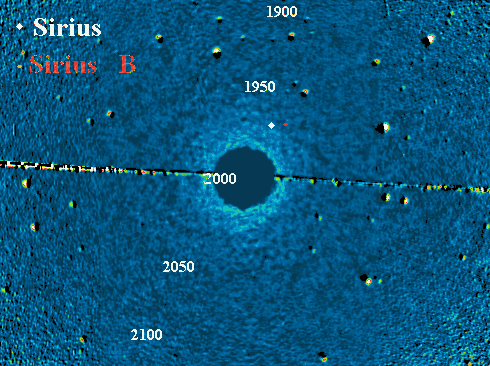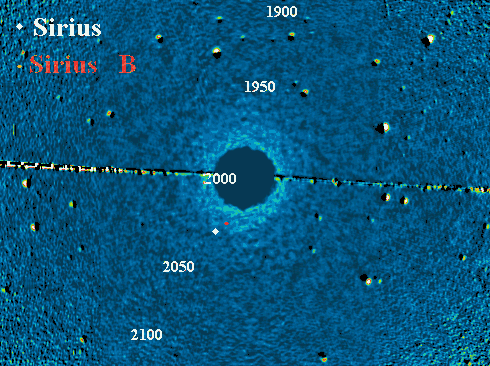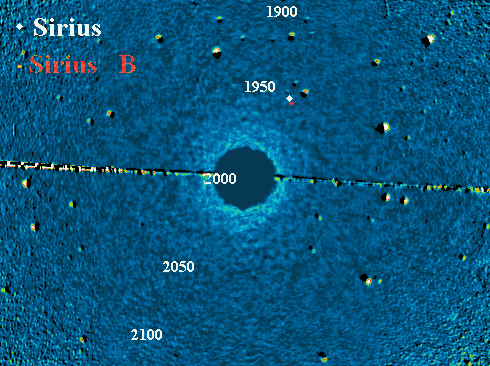
La dynamique de ce système stellaire Sirius A et B relève du problème à 2-corps.
La révolution orbitale (période de 50.1 ans, excentricité 0.59) se
superpose au mouvement apparent du système.
Crédit :
Observatoire du Pic du Midi
La galaxie M51 et son satellite

L'étude du mouvement relatif des 2 galaxies (M51 et son satellite)
relève en première approximation du problème à 2 corps, contrairement à la compréhension fine des
trajectoires stellaires individuelles.
Crédit :
CFHT
 Prérequis
Prérequis
Mécanique newtonienne ; interaction gravitationnelle
 Objectifs
Objectifs
Le but de cette page n'est pas de reprendre le formalisme du système à 2
corps (se référer à un cours de physique), mais de voir en quoi il est
fécond, et cerner son domaine de validité.
Le système à 2 corps : une approximation féconde
- Le problème à 2 corps peut être traité dans le référentiel
barycentrique du système. Comme le système est supposé isolé, ce
référentiel barycentrique est bien galiléen.
- La rotation des 2 corps l'un autour de l'autre, ou autour du
barycentre, peut être décrite
analytiquement
- Si un corps est de masse négligeable, on confond souvent le
barycentre du système avec le corps massif. Mais ça ne marche pas
toujours. La détection des exoplanètes
en est un contrexemple flagrant.
- Le problème à 2 corps, c'est le paradis des
lois de Kepler
Le problème à 2 corps : caractéristiques
- Le problème à 2 corps dénie toute structure aux 2 objets : ils
doivent être considérés comme de simples points matériels.
L' effet de marée ne se comprend qu'en introduisant la structure interne du corps qui subit la marée, càd un champ gravitationnel non uniforme.
- Le problème à 2 corps n'est qu'une approximation : sa validité peut être exemplaire à court terme, mais inopérante à long terme. Par exemple, l'avenir du système Terre-Lune ne peut être
précisément déterminé qu'en tenant compte des perturbations extérieures dues aux objets massifs du système solaire.
 La trajectoire de la Lune
La trajectoire de la Lune
Difficulté : ☆
Temps : 20 min
Le tableau ci-dessous présente
les caractéristiques orbitales de la Lune et de la Terre, ainsi que
| objet | masse 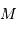 | distance 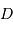 | distance 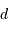 |
| (kg) | au soleil (km) | à la Terre (km) |
| Soleil | 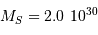 | | |
| Terre | 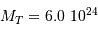 | 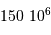 | |
| Lune | 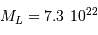 | 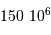 | 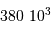 |
Question 1)
Déterminer l'énergie potentielle et la force d'interaction gravitationnelle entre le Soleil et la
Lune, puis entre la Terre et la Lune. Les calculer et les comparer.
Énergie d'interaction gravitationnelle : 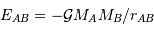 .
.
Force :
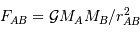
Question 2)
Autour de quel corps la Lune tourne-t-elle ?
Ne pas se laisser impressionner par la question.
Quel système apparaît le plus énergétiquement lié ?
- Question 1
Aide :
Énergie d'interaction gravitationnelle : 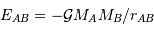 .
.
Force :
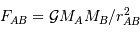
Solution :
En calculant les expressions des énergies d'interaction gravitationnelle entre 2 corps A et B :
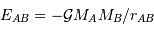
et de la force d'interaction gravitationnelle :
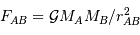
On peut remplir le tableau suivant :
| Interaction | Énergie d'interaction | Force |
| (J) | (N) |
| Soleil-Lune | 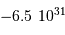 | 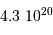 |
| Terre-Lune | 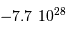 | 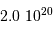 |
- Question 2
Aide :
Ne pas se laisser impressionner par la question.
Aide :
Quel système apparaît le plus énergétiquement lié ?
Solution :
La comparaison des énergies potentielles d'interaction gravitationnelle
montre que la Lune est plus liée au Soleil qu'à la Terre. On en déduit
que la Lune tourne autour du Soleil... comme la Terre. Et si l'on regarde
plus dans le détail, elle tourne aussi
autour de la Terre.
D'un point de vue "galiléen", la Lune est plus
liée au Soleil qu'à la Terre. Et sa trajectoire dans le référentiel héliocentrique est très proche d'un cercle (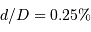 ).
).
D'un point de vue géocentrique, la Lune tourne autour de la Terre.





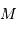
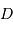
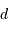
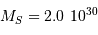
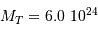
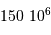
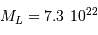
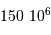
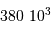
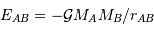 .
.
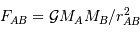
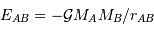
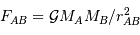
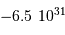
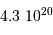
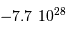
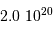
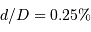 ).
).