 Objectifs
Objectifs
Les exemples de trajectoires quasi-circulaires autour d'un centre de force
sont légions, et méritent d'être étudiés de près. D'autant
plus que l'observation de paramètres liés au mouvement circulaire
autour d'un centre de force est un des nombreux moyens de peser les
objets de l'univers.
Vitesse orbitale
On considère un objet de masse négligeable, placé dans un potentiel
central de masse 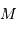 , sur une orbite circulaire de rayon
, sur une orbite circulaire de rayon 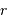 parcourue à la vitesse
parcourue à la vitesse
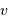 .
.
Le principe fondamental de la dynamique donne directement le lien entre
la vitesse 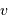 et le rayon
et le rayon 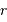 , en évaluant l'accélération centrale :
, en évaluant l'accélération centrale :
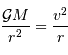
D'où la relation entre la vitesse et le rayon orbital :
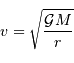
 QCM
QCM
 Phobos et Deimos
Phobos et Deimos
Difficulté : ☆
Temps : 20 min
Le tableau ci-dessous présente les caractéristiques orbitales des 2
satellites de Mars, Phobos et Deimos.
Satellites martiens
| Phobos | 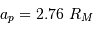 |
| Deimos | 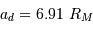 |
| Mars | 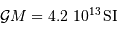 |
| 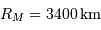 |
Question 1)
Calculer les vitesses orbitales des 2 satellites.
Question 2)
En déduire leurs périodes orbitales. Comparer à la journée martienne
(24.5 h) et conclure.
 Survol d'un satellite
Survol d'un satellite
Difficulté : ☆☆
Temps : 30 min
On cherche à évaluer la durée de transit d'un satellite artificiel en
orbite basse. On suppose l'horizon totalement dégagé, et
le satellite visible dès lors qu'il surmonte l'horizon.
On donne :
Données
| rayon terrestre | 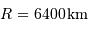 |
| masse de la Terre | 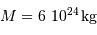 |
| altitude du satellite | 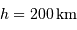 |
Question 1)
Estimer la vitesse et la période orbitale du satellite.
Voir le cours : c'est une des notions les plus importantes !
Question 2)
Faire un schéma montrant quelle portion de la trajectoire du satellite est visible.
Représenter la Terre, circulaire, et l'horizon, plan, de l'observateur, puis l'orbite du satellite.
Question 3)
Estimer la taille angulaire de cet arc de trajectoire. En déduire la
durée de visibilité du satellite.
Représenter la Terre, circulaire, et l'horizon de l'observateur.
 Vitesse circulaire / 3e loi de Kepler
Vitesse circulaire / 3e loi de Kepler
Difficulté : ☆
Temps : 10 min
Question 1)
Reprendre les expressions de la 3e loi de Kepler et de la vitesse
d'un objet en orbite circulaire autour d'un centre de force de
masse 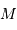 , et montrer, comme il s'agit de la même physique, que l'on peut les déduire l'une de l'autre.
, et montrer, comme il s'agit de la même physique, que l'on peut les déduire l'une de l'autre.
[2 points]
 Objets de Kuiper
Objets de Kuiper
Difficulté : ☆☆☆
Temps : 30 min
La recherche des objets lointains du système solaire, p.ex. les objets de Kuiper, est basée sur la détection de leur mouvement par rapport aux étoiles.

Mouvement apparent d'un objet de Kuiper sur 5 heures.
Crédit :
CFHT
Question 1)
Déterminer les vitesses orbitales, linéaire puis angulaire, d'un objet de Kuiper sur une orbite circulaire à 40 UA. Donner sa période de révolution sidérale.
[2 points]
Question 2)
Cette question s'intéresse au mouvement orbital autour du Soleil.
Déterminer la vitesse angulaire relative de l'objet par rapport à la Terre. Quel terme domine dans ce mouvement apparent ?
[3 points]
Question 3)
Déterminer le déplacement angulaire apparent sur fond de ciel de cet objet de Kuiper en 2 heures.
Quel est l'intérêt d'observer à l'opposition ?
[3 points]
Faire un schéma du triangle et notez qu'à l'opposition, la vitesse de la Terre est perpendiculaire à la direction de l'objet.
 Rotation dans une galaxie
Rotation dans une galaxie
Difficulté : ☆☆
Temps : 40 min
Un grand nombre de galaxies présentent un profil de luminosité qui varie en loi de puissance en fonction de la distance 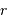 au centre galactique :
au centre galactique :
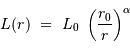
Cette donnée observationnelle permet d'écrire le profil de masse volumique de la galaxie sous la forme:
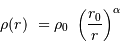
Question 2)
Déduire de 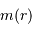 le champ gravitationnel
le champ gravitationnel 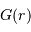 , ainsi que la vitesse de rotation circulaire au sein de la galaxie s'écrit :
, ainsi que la vitesse de rotation circulaire au sein de la galaxie s'écrit :
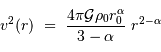
[2 points]
Le champ 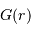 est sensible à la masse
est sensible à la masse 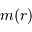 .
.
Question 3)
La plupart des galaxies montrent, pour large intervalle en rayon, un profil de vitesse plat. Quelle valeur de l'exposant 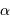 cette donnée observationnelle privilégie-t-elle ? Quelle conséquence pour le champ gravitationnel et la masse au rayon
cette donnée observationnelle privilégie-t-elle ? Quelle conséquence pour le champ gravitationnel et la masse au rayon 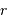 ?
?
[2 points]
Un profil plat est un profil indépendant de 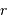 .
.
Question 4)
Dans le voisinage solaire, à 8.5 kpc du centre galactique, la vitesse de rotation est de l'ordre de 220 km.s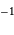 . En déduire la valeur de la masse galactique comprise
dans la sphère de rayon 8.5 kpc. La traduire en masse solaire. Cette valeur vous semble-t-elle plausible ?
. En déduire la valeur de la masse galactique comprise
dans la sphère de rayon 8.5 kpc. La traduire en masse solaire. Cette valeur vous semble-t-elle plausible ?
[3 points]
Quelle relation entre masse et rayon ?
Ce n'est ensuite qu'une application numérique !
- Question 1
Aide :
Voir le cours : c'est une des notions les plus importantes !
Solution :
Le rayon de la trajectoire est 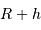 , d'où la vitesse orbitale
, d'où la vitesse orbitale
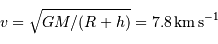 , et la période
, et la période
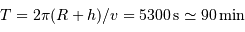 .
.
- Question 2
Aide :
Représenter la Terre, circulaire, et l'horizon, plan, de l'observateur, puis l'orbite du satellite.
Solution :
Le satellite est visible sur la portion de trajectoire située au-dessus de l'horizon.
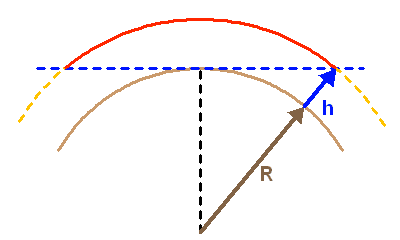
Crédit :
ASM
- Question 3
Aide :
Représenter la Terre, circulaire, et l'horizon de l'observateur.
Solution :
L'extension angulaire est 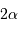 , avec
, avec 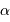 vérifiant
vérifiant
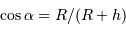 , d'où
, d'où 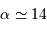 .
.
L'arc de cercle couvre 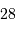 , soit 28/360 = 7.8% de la trajectoire
totale.
, soit 28/360 = 7.8% de la trajectoire
totale.
La durée du survol est donc de 7 minutes environ.
 Objectifs
Objectifs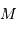 , sur une orbite circulaire de rayon
, sur une orbite circulaire de rayon 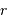 parcourue à la vitesse
parcourue à la vitesse
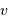 .
.
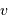 et le rayon
et le rayon 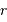 , en évaluant l'accélération centrale :
, en évaluant l'accélération centrale :
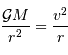
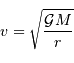
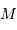 du centre de force. Rien d'étonnant à cela, il s'agit de la
même loi réécrite sous une autre forme (voir
exercice).
La mesure des 2 observables
du centre de force. Rien d'étonnant à cela, il s'agit de la
même loi réécrite sous une autre forme (voir
exercice).
La mesure des 2 observables 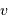 et
et 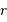 permet de déterminer la masse
permet de déterminer la masse 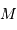 du centre de force, qui doit rendre compte de la relation:
du centre de force, qui doit rendre compte de la relation:
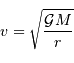
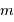 , dans le potentiel d'un corps
sphérique de masse
, dans le potentiel d'un corps
sphérique de masse 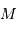
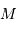 s'exprime ainsi:
s'exprime ainsi:
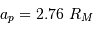
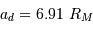
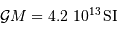
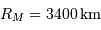
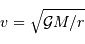
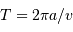
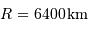
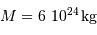
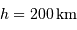
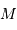 , et montrer, comme il s'agit de la même physique, que l'on peut les déduire l'une de l'autre.
, et montrer, comme il s'agit de la même physique, que l'on peut les déduire l'une de l'autre.

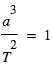 , où
, où 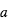 est le rayon de l'orbite et
est le rayon de l'orbite et 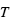 est la période.
est la période.
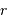 au centre galactique :
au centre galactique :
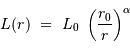
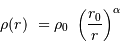
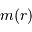 de la sphère galactique de rayon
de la sphère galactique de rayon 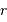 .
Montrer d'une part que la constante
.
Montrer d'une part que la constante 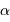 doit vérifier
doit vérifier 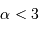 , d'autre part que le profil de masse volumique doit nécessairement être tronqué au delà d'un certain rayon.
, d'autre part que le profil de masse volumique doit nécessairement être tronqué au delà d'un certain rayon.
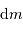 d'une coquille de rayon
d'une coquille de rayon 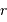 et épaisseur
et épaisseur 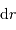 s'écrit
s'écrit 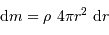
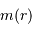 le champ gravitationnel
le champ gravitationnel 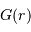 , ainsi que la vitesse de rotation circulaire au sein de la galaxie s'écrit :
, ainsi que la vitesse de rotation circulaire au sein de la galaxie s'écrit :
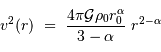
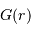 est sensible à la masse
est sensible à la masse 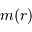 .
.
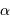 cette donnée observationnelle privilégie-t-elle ? Quelle conséquence pour le champ gravitationnel et la masse au rayon
cette donnée observationnelle privilégie-t-elle ? Quelle conséquence pour le champ gravitationnel et la masse au rayon 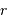 ?
?
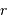 .
.
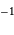 . En déduire la valeur de la masse galactique comprise
dans la sphère de rayon 8.5 kpc. La traduire en masse solaire. Cette valeur vous semble-t-elle plausible ?
. En déduire la valeur de la masse galactique comprise
dans la sphère de rayon 8.5 kpc. La traduire en masse solaire. Cette valeur vous semble-t-elle plausible ?
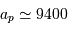 km pour Phobos et
km pour Phobos et 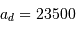 km pour Deimos.
Et leur vitesses orbitales sont alors respectivement, par application
de la loi
km pour Deimos.
Et leur vitesses orbitales sont alors respectivement, par application
de la loi  .
.
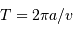 ,
respectivement 7h50 et 30h30. Phobos a une période orbitale plus courte
que la période de rotation propre de la planète : Phobos se lève à
l'ouest et se couche à l'est.
,
respectivement 7h50 et 30h30. Phobos a une période orbitale plus courte
que la période de rotation propre de la planète : Phobos se lève à
l'ouest et se couche à l'est.
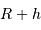 , d'où la vitesse orbitale
, d'où la vitesse orbitale
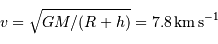 , et la période
, et la période
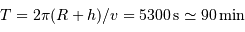 .
.

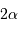 , avec
, avec 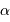 vérifiant
vérifiant
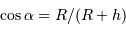 , d'où
, d'où 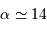 .
.
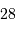 , soit 28/360 = 7.8% de la trajectoire
totale.
, soit 28/360 = 7.8% de la trajectoire
totale.