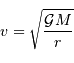|
Les exemples de trajectoires quasi-circulaires autour d'un centre de force sont légions, et méritent d'être étudiés de près. D'autant plus que l'observation de paramètres liés au mouvement circulaire autour d'un centre de force est un des nombreux moyens de peser les objets de l'univers.
On considère un objet de masse négligeable, placé dans un potentiel
central de masse 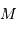 , sur une orbite circulaire de rayon
, sur une orbite circulaire de rayon 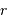 parcourue à la vitesse
parcourue à la vitesse
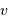 .
.
Le principe fondamental de la dynamique donne directement le lien entre
la vitesse 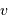 et le rayon
et le rayon 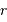 , en évaluant l'accélération centrale :
, en évaluant l'accélération centrale :
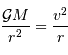
D'où la relation entre la vitesse et le rayon orbital :
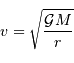
La relation donnant la vitesse orbitale en fonction du rayon d'une
orbite circulaire permet, comme la 3e loi de Kepler, de "peser" la
masse 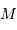 du centre de force. Rien d'étonnant à cela, il s'agit de la
même loi réécrite sous une autre forme (voir
exercice).
La mesure des 2 observables
du centre de force. Rien d'étonnant à cela, il s'agit de la
même loi réécrite sous une autre forme (voir
exercice).
La mesure des 2 observables 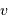 et
et 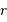 permet de déterminer la masse
permet de déterminer la masse 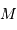 du centre de force, qui doit rendre compte de la relation:
du centre de force, qui doit rendre compte de la relation: