|
Nous venons de voir qu'il existait 2 types de miroirs sphériques : des miroirs concaves, comme un miroir de poche par exemple, qui ont la propriété de faire converger un faisceau lumineux ; des miroirs convexes, comme un rétroviseur, qui ont la propriété de faire diverger un faisceau lumineux.
Nous avons défini quatre points particuliers pour un miroir. Ces points sont appelés éléments cardinaux du miroir.
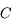 , centre de la sphère dans laquelle est découpé le miroir.
, centre de la sphère dans laquelle est découpé le miroir.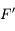 , image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet
, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet 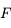 , antécédent d'un point situé à l'infini sur l'axe optique. Ils sont confondus dans le cas du miroir sphérique.
, antécédent d'un point situé à l'infini sur l'axe optique. Ils sont confondus dans le cas du miroir sphérique.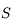 , intersection du miroir avec l'axe optique.
, intersection du miroir avec l'axe optique.
Les distances entre les points 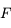 et
et 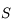 sont appelées distances focales. Ce sont des données du miroir. Elles caractérisent la vergence du miroir, c'est-à-dire son pouvoir de dévier les rayons lumineux.
sont appelées distances focales. Ce sont des données du miroir. Elles caractérisent la vergence du miroir, c'est-à-dire son pouvoir de dévier les rayons lumineux.
À l'aide de quatre rayons, il nous est désormais possible de tracer l'image d'un objet se reflétant sur le miroir. Le rayon lumineux passant par le centre revient sur lui-même, celui arrivant parallèle à l'axe optique ressort en croisant le foyer principal image, et celui passant par le foyer principal objet ressortira parallèle à l'axe optique. Enfin, le rayon frappant le miroir au sommet aura pour image son symétrique par rapport à l'axe optique.
Enfin, nous avons quelques relations qui nous permettront de calculer des tailles d'images, les distances où elles se forment et pourquoi pas des champs de vue et des grossissements. Ce sera pour bientôt.
Et on vient de voir en prime qu'un miroir plan est un miroir sphérique de rayon de courbure infini.