Complément : le cas limite du miroir plan

Auteur: Benjamin Mollier

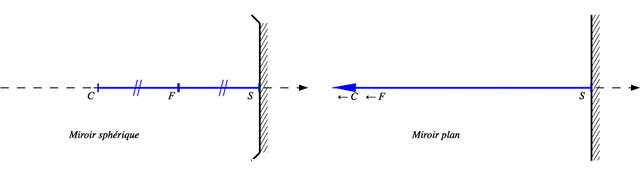
Que se passe-t-il si on prend un miroir sphérique et qu'on fait tendre son rayon de courbure vers l'infini ? Il devient plat.

Nous devrions donc pouvoir retrouver les propriétés du miroir plan à partir de celle du miroir sphérique, en faisant tendre 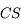vers l'infini.

La première conséquence est que la distance focale tend également vers l'infini, puisqu'elle vaut la moitié de 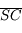$\overline{SC}$ .

Miroir plan

Un miroir plan est un miroir sphérique de rayon de courbure infini.

Crédit : ASM/B. Mollier

Grandissement

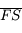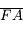$\overline{FS}$ et $\overline{FA}$ tendent vers l'infini. Or comme 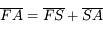$\overline{FA} = \overline{FS} + \overline{SA}$ , la longueur 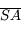$\overline{SA}$ devient très vite négligeable devant les deux autres. D'où 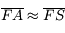$\overline{FA} \approx \overline{FS}$ et donc le grossissement tend vers 1.

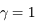
$\gamma = 1$

On retrouve bien le fait que notre image dans un miroir a la même taille et est dans le même sens.

Position de l'image

Où se situe l'image ? Prenons la relation de conjugaison de Descartes. Si la distance focale tend vers l'infini, alors 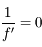$\frac{1}{f'} = 0$ . On a donc :

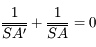
$\frac{1}{\overline{SA'}} + \frac{1}{\overline{SA}} = 0$

soit

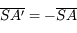$\overline{SA'} = -\overline{SA}$ .

L'objet et l'image sont équidistants du miroir.

Conclusion

En faisant tendre le rayon de courbure vers l'infini, nous venons de démontrer que le miroir plan possède un grandissement de 1, et que image et objet sont équidistants du miroir, autrement dit, ils sont symétriques l'un de l'autre.