Relation de conjugaison de Descartes |
Nous pouvons également obtenir une relation similaire, avec origine au sommet du miroir cette fois-ci. En partant de la formule du grandissement :
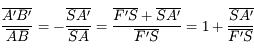
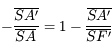
On obtient ainsi la relation de conjugaison de Descartes :
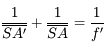
Remarque, on note parfois les distances 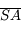 et
et 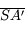 respectivement
respectivement 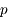 et
et 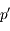 .
.
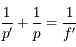
Là encore, les 2 relations de Descartes pour les lentilles et les miroirs ne se distinguent que par un signe  . Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc
. Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc 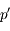 en
en 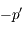 et
et 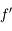 en
en 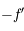 ...
...