Relation de conjugaison de Newton

Auteur: Benjamin Mollier

Grandissement : origines aux foyers

Et si on ne connaît pas la position de l'image ? Nous allons utiliser les foyers. En appliquant cette fois-ci le théorème de Thalès deux fois avec deux rayons différents, on obtient :

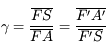
$\gamma = \frac{\overline{FS}}{\overline{FA}} = \frac{\overline{F'A'}}{\overline{F'S}}$

En introduisant les distances focale objet 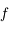et image 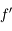, on obtient :

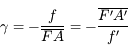
$\gamma = -\frac{f}{\overline{FA}} = -\frac{\overline{F'A'}}{f'}$

Crédit : ASM/B. Mollier

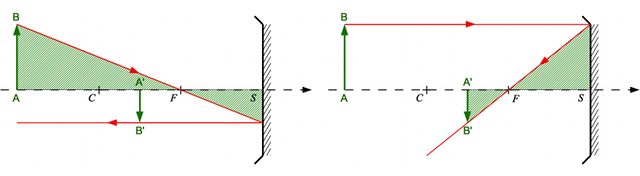
Et voilà, connaissant la distance focale et la distance de l'objet, on peut calculer le grandissement.

Relation de conjugaison de Newton (origines aux foyers)

Remarquons qu'à partir de ces deux formules, on va pouvoir calculer la distance de l'image.

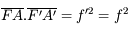
$\overline{FA}.\overline{F'A'} = f'^2 = f^2$

Nous venons d'établir la relation de conjugaison de Newton. Elle est aussi appelée relation de conjugaison avec origine au foyer, car les distances de l'objet et de l'image sont comptées à partir des foyers principaux.

Remarque

Au signe près, elle est identique à celle des lentilles minces.

Aurait-on pu retrouver cette relation justement à partir de celle établie au chapitre sur les lentilles ? Oui, si on se souvient qu'il suffit de "plier" notre dessin pour passer des lentilles aux miroirs. Le pliage change le signe de 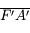$\overline{F'A'}$ . Ce qui explique la perte du signe dans la relation de conjugaison de Newton.