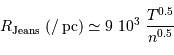 |  |  |  |  |  |
|
ObjectifsÀ quelles conditions un nuage se condense-t-il ? Le critère de Jeans donne une réponse liant la masse ou le rayon limite du nuage à sa densité particulaire et sa température.
Un nuage s'effondre si, perturbé, son énergie mécanique devient négative :
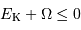
On en déduit une relation sur la masse limite du nuage, fonction de la température (pour l'agitation cinétique) et de la densité (pour la tendance à la contraction). Une masse supérieure à cette masse limite va conduire à la contraction du nuage.
On suppose le milieu homogène et uniforme, et donc le lien entre masse et rayon est simplement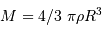 
. On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
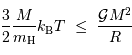
On poursuit le calcul en ne s'intéressant qu'à la dépendance en fonction des variables (ceci permet d'alléger les calculs, et de s'affranchir des constantes numériques qui ne sont de toutes façons pas correctement estimées dans une approche simplifiée). En substituant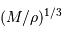 
à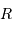 
, le cas limite de l'égalité précédente donne une dépendance :
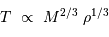
On en déduit la masse limite du nuage, appelée masse de Jeans, qui dépend de la température et de la densité du nuage, au-delà de laquelle un nuage est amené à s'effondrer :
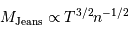
Plus le nuage est chaud, plus il peut être massif avant de s'effondrer : la pression cinétique l'aide à se maintenir. A contrario, plus il est dense, plus la masse de Jeans baisse, en raison d'un potentiel gravitationnel, attractif, croissant avec la masse.
En unité de masse solaire, la masse de Jeans devient :
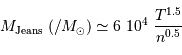
La limite d'effondrement peut également s'exprimer via le rayon du nuage, toujours en fonction de la température du nuage et de sa densité.
 |  |
Apprendre