Avant d'aborder des systèmes optiques plus complexes, il est temps de faire un point sur les notions de source de lumière, d'objet et d'image.
Sources primaires ou secondairesL'oeil voit les objets parce qu'ils nous envoient de la lumière. Il est nécessaire que cette dernière parte d'eux et arrive jusqu'à notre oeil. Certains objets, comme une lampe, une bougie ou une étoile, produisent leur propre lumière. On parle de source primaire. D'autres sources, comme un livre, un tableau, une photo... ne produisent pas de lumière. Pourtant nous parvenons à les voir. C'est parce qu'ils réfléchissent ou diffusent la lumière environnante. Si on éteint la lumière, ils deviennent invisibles. On parle alors de source secondaire, car ils réfléchissent la lumière d'une source primaire.
| Sources primaires | Sources secondaires |
| Soleil, étoile | Lune, planètes |
| Lampe, bougie | Mur, plafond |
| Écran de téléviseur | Tableau, photo |
| Laser |
Attention, un miroir, une lentille, ou tout autre instrument d'optique n'est pas considéré ici comme un objet. S'ils sont propres, ils sont parfaitement transparents et invisibles. Ils ne diffusent pas la lumière et on ne les voit pas.
Sources ponctuelles ou étenduesUn objet peut être ponctuel (on en voit donc qu'un point, comme une étoile par exemple) ou étendu (c'est alors un ensemble de point, comme la Lune).
Sources proches ou à l'infiniUn objet peut être à distance finie, proche de nous (l'oeil doit alors accommoder pour le voir net, mais nous y reviendrons au chapitre consacré aux instruments) ou à l'infini (tous les rayons lumineux issus d'un point nous arrivent parallèles entre eux. On n'a plus besoin d'accommoder pour le voir net).
Un objet à distance finie peut être défini par sa taille. Pour un objet à l'infini, cela n'a plus vraiment de sens. La Lune et le Soleil, tous deux à l'infini, nous apparaissent comme ayant la "même taille" (ce qu'on vérifie aisément lors des éclipses solaires), pourtant le Soleil est bien plus grand que la Lune. Mais comme il est beaucoup plus loin... Il est pertinent d'introduire une nouvelle notion, celle de taille angulaire (ou diamètre apparent). Il est défini comme étant l'angle sous lequel on voit l'objet :
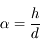
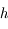étant la taille de l'objet, et 
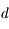sa distance. Cette relation n'est valable que lorsque 
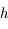est très petit devant 
(
).
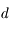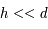Le diamètre apparent de la Lune vaut :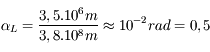 
° et celui du Soleil 
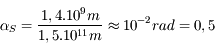° d'où 
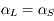et c'est pour cela qu'il y a des éclipses totales !
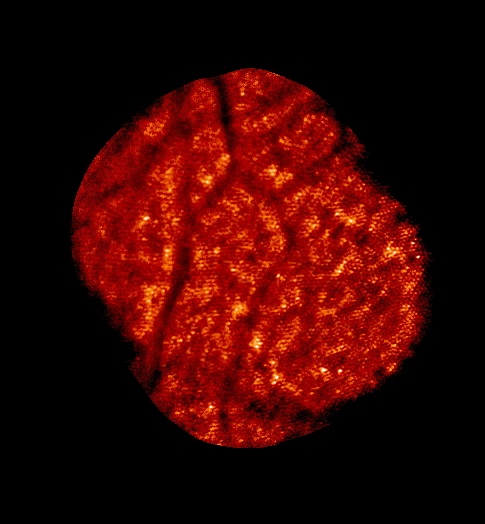
Un récepteur est constitué d'éléments photosensibles, c'est-à-dire d'éléments qui délivrent un signal en fonction de l'éclairement dans un domaine spectral donné.
La rétine de l'oeil, une photodiode ou un capteur CCD sont quelques exemples de récepteurs. La bonne vieille pellicule photo aussi. Mais contrairement aux autres ci-dessus, ce n'est pas un signal électrique qui est délivré, mais un réaction chimique qui "imprime" le négatif.
Ces récepteurs simples peuvent être couplés avec des systèmes optiques : l'objectif d'un appareil photo ou le cristallin de l'oeil par exemple.
.
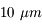Servons nous d'un miroir plan, que nous avons étudié précédemment, pour définir les notions d'objet et d'image pour un système optique.
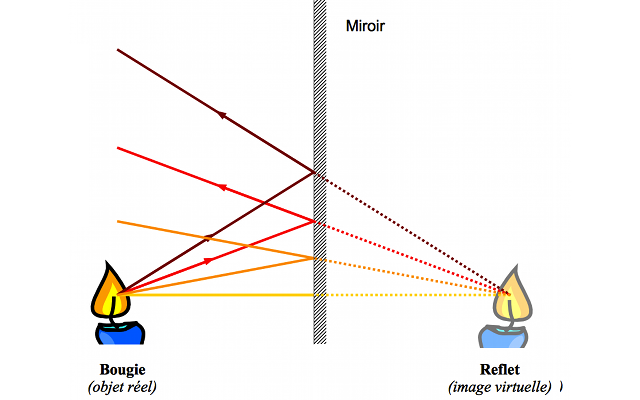
Nous disposons d'une bougie et d'un miroir plan. On place celle-ci devant le miroir. On peut voir la bougie ainsi que son reflet, son image, à travers le miroir. Pour simplifier notre étude, nous assimilerons la bougie à un unique point lumineux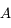 
. La bougie constitue un objet par rapport au système optique "miroir". Les rayons lumineux issus de cet objet divergent au niveau du plan du miroir. Nous qualifierons cet objet, placé en amont du système optique, de réel. On peut le toucher (mais ça brûle...).
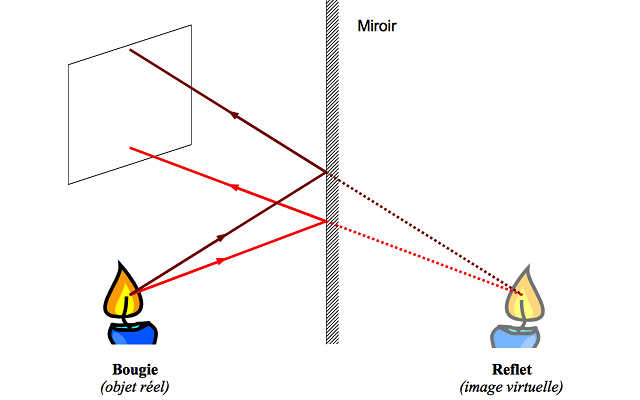
Objet réelTout objet placé en amont d'un système optique, dans le sens de propagation de la lumière, est un objet réel.
Intéressons nous maintenant à son reflet dans le miroir. Les rayons lumineux issus de la bougie sont réfléchis par la surface du miroir et semblent provenir d'un point point situé derrière le miroir. Le faisceau issu de ce point diverge. Il est impossible de faire l'image de ce point sur un écran. L'image est qualifiée de virtuelle.
Image virtuelleToute image placée en amont du système optique est virtuelle.
On troque notre bougie contre une lampe torche, dont le faisceau converge en un point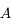 
. Le point sera notre objet. Si on place un écran là où converge le faisceau, on voit une petite tache lumineuse.
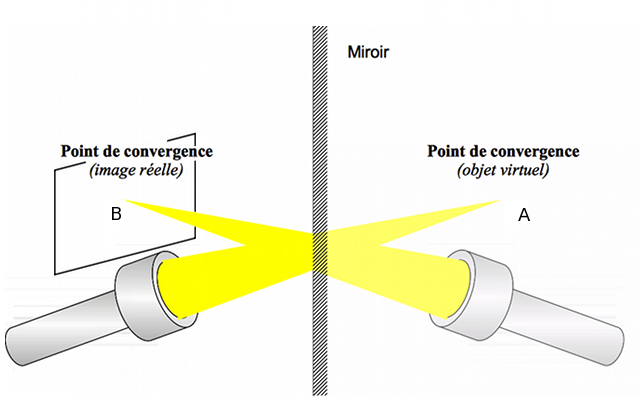
Objet virtuelSi on intercale le miroir entre notre lampe et cet écran, la tache disparaît. Mais malgré le miroir, le faisceau semble converger vers cet écran, vers un point situé à l'arrière du miroir. Ce point est toujours notre objet, mais il est désormais virtuel, car situé en aval du système optique. On ne peut plus le toucher.
Image réelle
Le faisceau réfléchi par le miroir converge en un point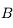 
. Si on place un écran au niveau de celui-ci, nous voyons s'y former une tache lumineuse. L'image est cette fois-ci réelle.
Soit un système optique quelconque. Le sens de propagation de la lumière nous permettra de définir l'espace en amont du système optique (avant que la lumière n'y rentre) et en aval (une fois qu'elle y est ressortie).
En traçant le prolongement des rayons réfractés, on s'aperçoit que l'image est virtuelle, car située en amont du dioptre. On remarque cependant, qu'en traçant de nombreux rayons, tous ne convergent pas au même point, mais dans une petite zone. Par contre, la même expérience avec un miroir plan nous montre que tous les rayons convergent en un seul point. Nous venons de mettre le doigt sur la notion de stigmatisme, très importante en optique lorsqu'on cherche à obtenir des images nettes.
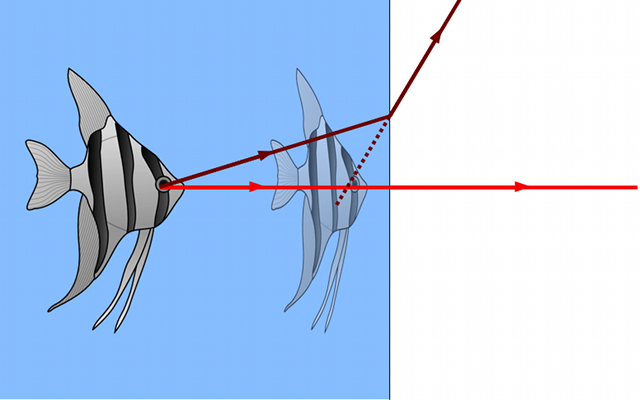
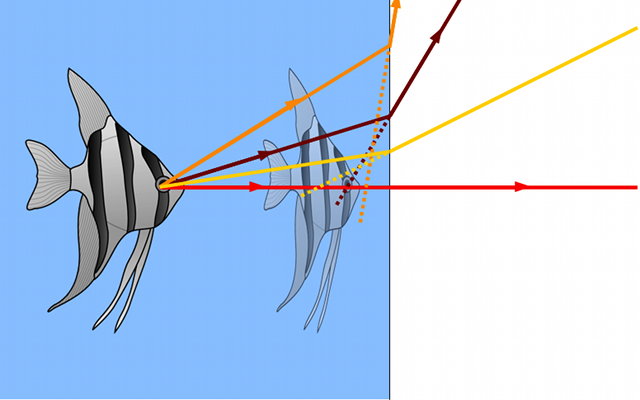
Nous venons de voir qu'en fonction des systèmes optiques, l'image d'un point est soit exactement un point (tous les rayons issus d'un point convergent en un seul point image), ou soit une tache (tous les rayons ne convergent pas tous en un seul point, mais dans une petite zone).
StigmatismeLorsque, à travers un système optique, l'image de chaque point objet est un point, on dit que le système est rigoureusement stigmatique. On parle de stigmatisme approché si l'image d'un point est une petite tache. La notion de stigmatisme approché est assez subjective. Elle dépend également du récepteur utilisé pour voir l'image. On tolérera plus facilement un système avec un stigmatisme approché si le récepteur possède de gros pixels (surtout s'ils sont plus gros que la tache image) que s'il possède de petits pixels.
Un système est dit aplanétique si l'image d'un objet perpendiculaire à l'axe optique (l'axe de symétrie du système) est elle aussi perpendiculaire à ce dernier.
Cette définition ne vous parle pas pour l'instant, mais elle prendra tout son sens au chapitre suivant.
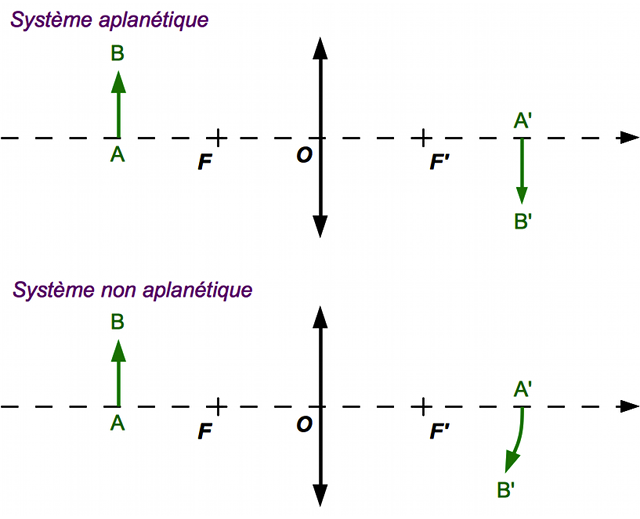
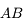est perpendiculaire à l'axe optique. Dans le cas du haut, l'image 
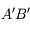est elle aussi perpendiculaire à l'axe optique, le système est aplanétique. Dans le cas du bas, elle n'est pas perpendiculaire à l'axe, elle est tordue. Le système n'est pas aplanétique.
Mise en évidenceSoit un faisceau de lumière constitué de plusieurs rayons lumineux. Si on les fait traverser une lentille, on constate qu'ils convergent. Ils convergent, certes, mais pas tous au même point. Nous ne sommes pas en condition de stigmatisme rigoureux.
Si on diaphragme le faisceau lumineux, c'est-à-dire si on l'ampute de ses rayons extérieurs, on constate que la condition de stigmatisme est beaucoup mieux respectée.
Nous venons de mettre en évidence les conditions de Gauss.
Conditions de GaussLes conditions de Gauss, ou l'approximation de Gauss, sont obtenues lorsque les rayons lumineux possèdent un angle d'incidence très faible par rapport à l'axe optique, et en sont peu éloignés. Ils sont dits paraxiaux.
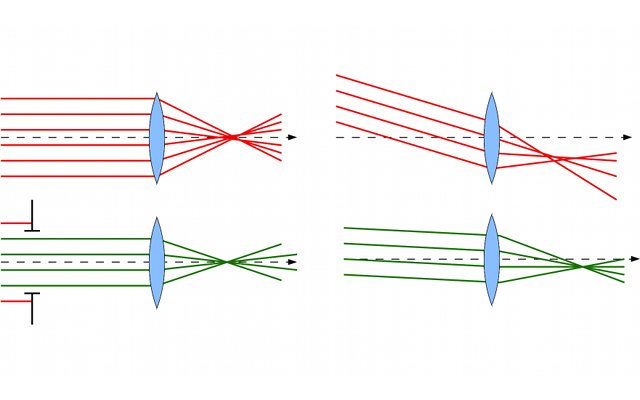
Dans ces conditions, les conditions de stigmatisme et d'aplanétisme sont en général respectées.
Pour les obtenir, il suffit en général de placer un fort diaphragme en entrée du système.
RemarquesDans les chapitres suivants, nous nous placerons dans ces conditions.
Si ces conditions permettent d'obtenir un bon stigmatisme et aplanétisme, elles ne sont en général pas recherchées par les opticiens. Le grand inconvénient de ces conditions est qu'à cause du diaphragme, on obtient peu de lumière et un champ de vue très restreint. C'est le contraire que l'on recherche en astronomie et en photographie. Toute la difficulté consiste donc à corriger toutes les aberrations optiques pour retrouver du stigmatisme et de l'aplanétisme. C'est pour cela qu'il y a tant de lentilles (une dizaine) dans un simple objectif photo.
Système optique
appelé axe optique du système.ObjetObjet primaire/secondaireUn objet n'est visible que s'il émet ou diffuse la lumière.
ponctuel/étenduObjet réel/virtuelImage
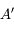est l'image de 
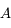à travers un système optique, alors 
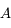est l'antécédent de 
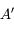par ce même système. Dans des conditions de stigmatisme, 
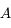et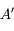 
sont des points. Ils sont conjugués l'un de l'autre.Image ponctuelle/étendueImage réelle/virtuelleConditions de GaussOn se placera par la suite dans les conditions de Gauss : les rayons entrant dans les systèmes optiques seront paraxiaux.
Prérequis