L'équilibre hydrostatique global

Auteur: Arnaud Beck

Pour obtenir une équation globale, multiplions chaque membre de l'équation par le volume

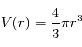
$V(r)=\frac{4}{3}\pi r^3$

et intégrons le résultat entre r=0 et r= 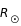R_soleil .

Le membre de droite donne :

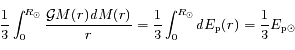
$\frac{1}{3}\int_0^{R_{\odot}}\frac{\mathcal{G}M(r)dM(r)}{r}=\frac{1}{3}\int_0^{R_{\odot}}dE_{\rm p}(r)=\frac{1}{3}E_{\rm p \odot}$

Où E_p est l'énergie potentielle gravitationnelle et 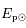$E_{\rm p\odot}$ l'énergie potentielle gravitationnelle totale du Soleil.

Le membre de gauche donne :

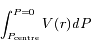
$\int_{P_{\rm centre}}^{P=0} V(r)dP$

où P_centre est la pression au centre du Soleil et en supposant que la pression est nulle à sa surface. Une intégration par partie donne :

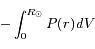
$-\int_{0}^{R_{\odot}}P(r)dV$

En faisant l'hypothèse des gaz parfaits on a : PV=Nk_BT où N est le nombre totale de particules dans le système et k_B la constante de Boltzman. En remarquant que l'énergie interne du système s'écrit 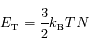$E_{\rm T}=\frac{3}{2}k_{\rm B}TN$ , on peut récrire l'équation des gaz parfaits en :

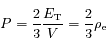
$P=\frac{2}{3}\frac{E_{\rm T}}{V}=\frac{2}{3}\rho_{\rm e}$

où ρ_e est la densité volumique d'énergie interne. En la réinjectant dans l'équation précédente le membre de gauche donne finalement :

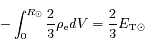
$-\int_0^{R_{\odot}}\frac{2}{3}\rho_{\rm e}dV=\frac{2}{3}E_{\rm T\odot}$

où 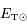$E_{\rm T \odot}$ est l'énergie interne totale du Soleil. Au final, l'équation d'équilibre hydrostatique intégrée donne donc :

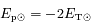$E_{\rm p\odot}=-2E_{\rm T\odot}$ .

Cela signifie que si le Soleil se contracte et que son énergie potentielle diminue de ΔE_p, son énergie thermique augmente de ΔE_T=ΔE_p/2 et le Soleil se réchauffe. Pendant une contraction, la moitié de l'énergie potentielle gravitationnelle en jeu est donc convertie en énergie interne. L'autre moitié est en fait évacuée sous forme de rayonnement.