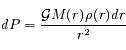L'équilibre hydrostatique local de l'intérieur

Auteur: Arnaud Beck

Supposons que le Soleil soit tout simplement une boule de gaz à l'équilibre hydrostatique. C'est-à-dire que le Soleil est une boule de rayon 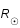R_soleil , au repos, et dont la température T , la densité ρ et la pression P ne dépendent que du rayon r où l'on se place.

Étudions un élément infinitésimal cylindrique de cette boule. Cet élément, situé à une distance r du centre du Soleil, est de section ds et de hauteur dr. Sa densité est celle du milieu environnant, ρ(r), et sa masse vaut dm = ρ(r) dr ds (voir figure ci dessous) :

Crédit : Arnaud Beck, LESIA

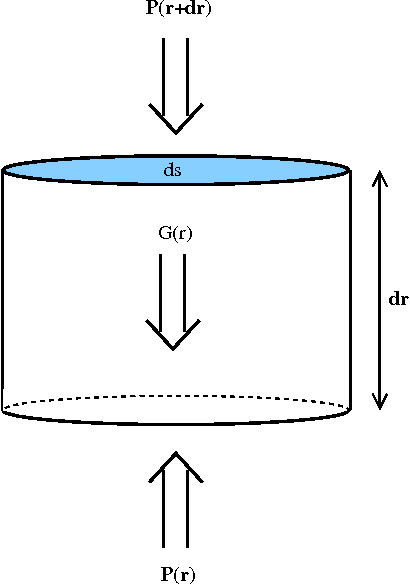
Trois forces s'exercent sur ce cylindre de gaz. Deux forces de pression P(r)ds et P(r+dr)ds ainsi que le poids du cylindre :

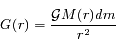
$G(r)=\frac{\mathcal{G}M(r)dm}{r^2}$

où 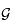$\mathcal{G}$ est la constante universelle de gravitation et M(r) est la masse totale contenue dans la sphère de rayon r, soit :

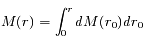
$M(r)=\int_0^r dM(r_0)dr_0$

avec

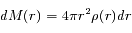
$dM(r)=4\pi r^2\rho(r)dr$

Supposer que le Soleil est au repos implique que la somme des forces s'exerçant sur ce cylindre est nulle. C'est-à-dire que la différence entre les forces de pression est exactement équilibrée par la force de gravité. On a donc l'équation d'équilibre hydrostatique locale :

$dP=\frac{\mathcal{G}M(r)\rho (r)dr}{r^2}$