Force de Coriolis

Auteurs: Thomas Navarro, Arianna Piccialli

Dans un référentiel en rotation, une autre force apparente est à prendre en compte lors d'un déplacement. Il s'agit de la force de Coriolis, qui tient compte du fait que le déplacement d'une particule génère une accélération apparente supplémentaire. Par exemple, le mouvement rectiligne d'une particule est apparement dévié pour un observateur situé dans un référentiel tournant.

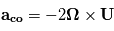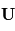L'accélération de la force de Coriolis s'exprime $\mathbf{a_{co}}}=-2\mathbf{\Omega}\times\mathbf{U}$ avec $\mathbf{U}$ le vecteur vitesse de la parcelle d'air considérée.

La vitesse 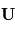$\mathbf{U}$ d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en général petite par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :

A l'équateur l'accélération de Coriolis est orientée selon l'axe radial, c'est-à-dire vers le haut ou vers le bas.
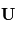
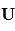
Dans l'hémisphère Nord, sa projection sur le plan de la surface locale est orientée à droite du vecteur vitesse $\mathbf{U}$
Dans l'hémisphère Sud, sa projection sur le plan de la surface locale est orientée à gauche du vecteur vitesse $\mathbf{U}$

Ceci explique pourquoi certaines structures atmosphériques, tels les ouragans ou les anticyclones, tournent toujours dans le sens des aiguilles d'une montre dans l'hémisphère Nord, et dans le sens contraire dans l'autre hémisphère.

Exercice de démonstration et d'acquisition du cours

Question 1)

Démontrer par l'analyse ou par un schéma en 3D les 3 points ci-dessus.