
Coordonnées sphériques |
Comme toute équation de la physique, les équations régissant la dynamique atmosphérique doivent s'exprimer dans un système de coordonnées et un référentiel choisis arbitrairement. Un tel système naturellement adapté à une sphère, et donc à une planète, sont les coordonnées sphériques 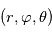 , où
, où 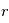 est la distance au centre de la sphère,
est la distance au centre de la sphère, 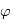 est la l'angle de la longitude, et
est la l'angle de la longitude, et 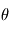 est l'angle de la latitude.
est l'angle de la latitude.
On définit également un repère local pour tout point de l'espace de coordonnées 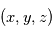 , avec comme base le triplet
, avec comme base le triplet 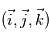 où
où 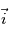 est dirigé vers l'Est,
est dirigé vers l'Est, 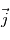 dirigé vers le Nord, et
dirigé vers le Nord, et 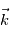 selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
Pour résumer, on travaille dans deux référentiels différents, ce qui donne trois systèmes de coordonnées différents :
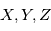 ).
).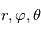 ).
).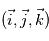 , qui est un système de coordonnées cartésiennes.
, qui est un système de coordonnées cartésiennes.L'exercice suivant permet de se familiariser avec la manipulation mathématique des coordonnées et des repères. Les resultats serviront à établir l'équation fondamentale de la dynamique.
Montrer que dans le référentiel de la planète, un point de coordonnées sphériques 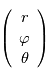 a pour coordonnées cartésiennes
a pour coordonnées cartésiennes 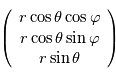
Exprimer 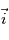 ,
, 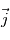 et
et 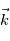 dans le repère de la planète en fonction des angles
dans le repère de la planète en fonction des angles 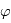 et
et 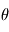
Montrer qu'une vitesse dans le référentiel local 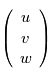 au point de coordonnées sphériques
au point de coordonnées sphériques 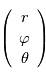 s'exprime par
s'exprime par 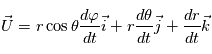 .
.
Exprimer 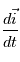 ,
, 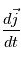 et
et 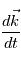 en fonction de
en fonction de 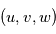 ,
, 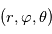 et
et 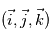 .
.