 |  |  |  |  |  |
Appliquette Migration |
En raison de la grande volatilité de la glace, les surfaces glacées sans atmosphère sont soumises à un phénomène de migration/ségrégation thermique. L’appliquette ci-dessous vise à évaluer l’efficacité de ce phénomène par rapport à d’autres processus d’érosion spatiale sur les principaux satellites glacés du Système Solaire. Elle s’inspire du travail de thèse de J.R. Spencer: The surfaces of Europa, Ganymède, and Callisto- An investigation using Voyager IRIS Thermal Infrared Specta, Ph.D dissertation by John R. Spencer, 1999.
Lisez l’essentiel à savoir ci-dessous et essayez de répondre aux questions.
Le taux instantané de sublimation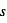 
de la glace peut, en première approximation, s’exprimer de la façon suivante : 
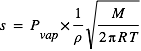où 
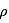est la densité volumique de la glace (
), 
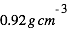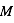est la masse molaire de l'eau (
), 
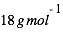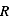est la constante universelle des gaz parfaits (
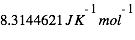) et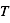 
, la température instantanée (en K).
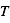s’obtient en égalisant le flux solaire (entrant) et le flux émis par la surface (sortant) : 
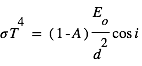où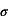 
est la constante de Stefan-Boltzmann (
), 
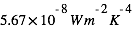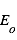est la constante solaire (c’est-à-dire la puissance reçue du Soleil par unité de surface normale aux rayons solaires à la distance héliocentrique de 1 UA) (
), 
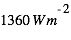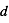est la distance héliocentrique en UA du corps glacé, 
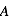est est l’albédo de la surface et 
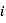est l’angle d’illumination du Soleil à la surface (l’angle entre la normale à la surface et la direction de l’ensoleillement). Il dépend de la latitude, de l’heure locale et éventuellement de la saison. Ici on considère que 
.
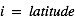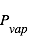est la pression de vapeur saturante de la glace en Pascal, c’est-à-dire la pression à laquelle la phase gazeuse de l’eau est à l’équilibre avec sa phase solide à la température 
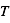. Dans la gamme de températures des satellites glacés du système solaire (130-150 K), il a été établi semi-empiriquement que : 
.
Questions
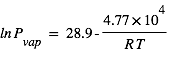Mise en jambe : par une analyse dimensionnelle, retrouvez la dimension de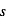 
?
Comparez l’amplitude du phénomène de ségrégation thermique entre les satellites galiléens (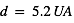
), les satellites saturniens (
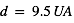) et ceux d’Uranus (
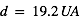). Vous vous placerez à l’Equateur, à midi, en été et prendrez un albédo de 
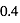pour la glace équatoriale.
Tracez le taux de sublimation lié au phénomène de ségrégation thermique en fonction de la latitude et de l’albédo de la glace pour un satellite galiléen. Comparez son intensité sur Europa (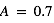
), Ganymède (
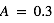) et Callisto (
).
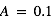À quelle(s) latitude(s) ce phénomène est-il le plus actif ?
Dans le système de Jupiter, la vitesse de « laboure » des régolithes par impacts micro-météoritiques est de quelques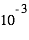 
mm/an. L’intensité du phénomène de « sputtering », quant à elle, décroit avec la distance à Jupiter : 
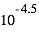mm/an sur Europe, 
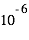mm/an sur Ganymède et 
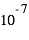mm/an sur Callisto. Que peut-on en déduire sur l’efficacité du phénomène de ségrégation thermique sur Europe, Ganymède et Callisto ? Discutez.
 |  |
où 
est la dimension d'une distance et 
celle d'un temps.