
|
Cette page développe de façon quantitative les notions vues de façon qualitative ici.
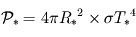
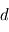 la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice)
la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice) 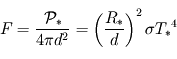
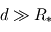 ), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux
), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux 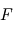 par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon
par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon 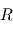 de la planète, d'où
de la planète, d'où 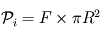
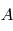 , la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit
, la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit 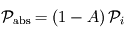 .
.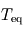 se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors
se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors 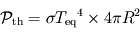 puisque l'ensemble de la planète rayonne.
puisque l'ensemble de la planète rayonne.Le bilan radiatif à l'équilibre imposant l'égalité entre la puissance rayonnée par la planète et la puissance absorbée par la planète, on obtient alors l'équation suivante :
![\[ \pi R^2 \left(1 - A \right) F = 4 \pi R^2 \sigma {T_{\mathrm{eq}}^4 \]](../pages_planetologie-thermique/equations_fluide-temperature-comprendre-noatm/equation50.png)
qui se résout directement, après simplification du rayon 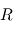 de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
![T_{\mathrm{eq}} = \left[ \frac{\left(1 - A\right) F}{4 \sigma} \right]^{1/4} = \sqrt{\frac{R_*}{d}} \left( \frac{1-A}{4} \right)^{1/4} T_*](../pages_planetologie-thermique/equations_fluide-temperature-comprendre-noatm/equation52.png)
ce qui permet de constater que cette température décroît avec la distance à l'étoile, et est proportionnelle à celle de l'étoile. Ainsi, toutes choses égales par ailleurs, pour une étoile naine rouge d'une température moitié de celle du Soleil, il faut pour conserver une température d'équilibre donnée se rapprocher de l'étoile d'un facteur quatre : on peut d'ores et déjà affirmer que les zones habitables autour des petites étoiles de faible température (naines rouges) sont très proches de ces dernières. Notons au passage que la température d'équilibre d'une planète est bornée par celle de son étoile, plus précisément comprise entre 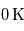 (à très grande distance) et
(à très grande distance) et 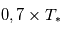 à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).
à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).