
|
Nombre de sources astrophysiques présentent un diamètre angulaire qui ne peut pas être résolu par une pupille unique. Mais l'interférométrie permet d'affiner la résolution angulaire, et de mesurer des diamètres stellaires.
Le diamètre d'une étoile du proche environnement solaire sous-tend un angle de l'ordre d'une milliseconde d'arc. Ce diamètre est, sauf exception, très inférieur à la largeur de la tache de diffraction dans le visible d'un télescope, même de grand diamètre. En revanche, par interférométrie, on peut avoir accès indirectement à ce diamètre, si l'on dispose d'une base suffisamment grande.
On suppose une source de brillance uniforme, circulaire de diamètre angulaire
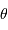 , observée par 2 télescopes identiques séparés d'une base
, observée par 2 télescopes identiques séparés d'une base
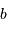 (base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
(base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
Le facteur de cohérence établi dans le cas général est usuellement dénommé visibilité. La fonction de visibilité s'écrit :
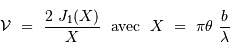
où 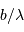 est la fréquence spatiale.
est la fréquence spatiale.
Chaque base 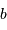 conduit à une mesure de la visibilité pour la fréquence spatiale
conduit à une mesure de la visibilité pour la fréquence spatiale 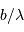 . Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour
. Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour 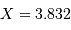 , et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
, et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
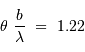
Finalement, une mesure du diamètre stellaire 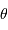 revient à une mesure de visibilité de la figure d'interférence.
revient à une mesure de visibilité de la figure d'interférence.
Le calcul précédent a supposé que la source présente un profil de brillance uniforme : en fait le phénomène d'assombrissement centre-bord complique un peu l'analyse. Le rôle de la diffraction ne peut bien sûr pas être négligé : toute mesure de visibilité doit être corrigée de la fonction d'appareil des collecteurs (dont la diffraction), que l'on détermine expérimentale sur une source vraiment ponctuelle (en pratique : très lointaine).
Une pupille unique est un filtre passe-bas, coupant à la fréquence spatiale 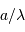 , et donnant une résolution angulaire de
, et donnant une résolution angulaire de 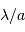 .
.
Un interféromètre est donc un filtre passe-bande, qui fournit une information à la fréquence 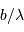 ; sa résolution angulaire est
; sa résolution angulaire est 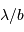 .
.
On retrouve ces propriétés par une analyse en terme de Fourier : le théorème de Wiener-Khintchine relie la fonction de transfert optique à la TF inverse de l'autocorrélation de la pupille.
Une mesure du facteur de cohérence complexe fournit une composante de fréquence spatiale de la source. La mesure de ce facteur à plusieurs fréquences spatiales permet la reconstruction de la distribution spatiale d'intensité de la source.