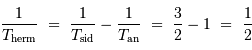Les observations du ciel sont effectuées, pour la plupart, depuis la Terre.
Les mesures qui en résultent sont analysées, pour la plupart, dans un référentiel héliocentrique, le référentiel géocentrique n'offrant pas un cadre suffisamment galiléen (référentiel dans lequel un corps soumis à aucune force est en mouvement rectiligne uniforme) .
Les pages de cette section traitent des changements entre les différents référentiels utiles à l'astronomie et à l'astrophysique.
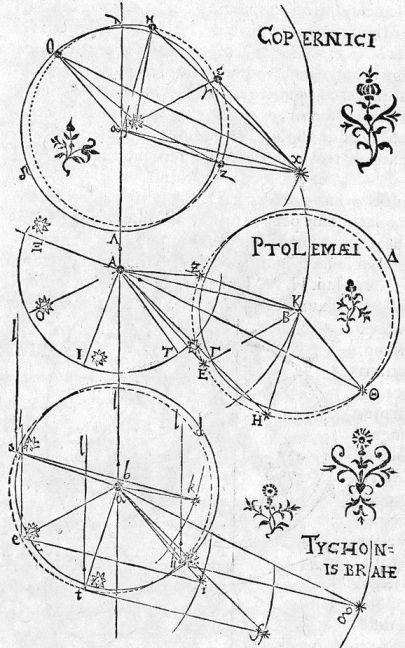
Trois façons de voir l'Univers, selon les astronomes Copernic, Ptolémée et Tycho Brahe.
Crédit :
Bibliothèque de l'Observatoire de Paris
 Objectifs
Objectifs
Passer des coordonnées équatoriales, données par les catalogues, aux coordonnées azimutales, liées au lieu d'observation.
 Visibilité
Visibilité
Difficulté : ☆
Temps : 40 min
D'après les équations de changement de système de coordonnées, un astre est levé si sa hauteur 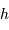 est positive, ce qui signifie :
est positive, ce qui signifie :
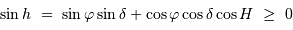
(voir la page cours pour le rappel de la définition des symboles).
Ceci conduit à une condition sur l'angle horaire :
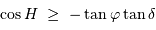
qui doit pouvoir être satisfaite.
Question 1)
Dans quel cas cette équation n'admet-elle jamais de solution ?
Dans quel domaine de valeurs 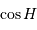 peut-il varier ?
peut-il varier ?
Question 2)
Dans quel cas cette équation admet-elle toujours une solution ?
Se baser sur la question précédente
Question 3)
Représenter, pour un lieu de latitude 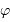 moyenne, un diagramme avec les étoiles circumpolaires (une étoile circumpolaire est suffisamment proche du pôle pour ne jamais descendre sous l'horizon) et les étoiles toujours invisibles.
moyenne, un diagramme avec les étoiles circumpolaires (une étoile circumpolaire est suffisamment proche du pôle pour ne jamais descendre sous l'horizon) et les étoiles toujours invisibles.
 Objectifs
Objectifs
Un référentiel, c'est aussi une horloge. La période apparente d'un phénomène périodique dépend donc de cette horloge.
Changer de référentiel, c'est changer de point de vue !
Comme ici, les différents référentiels concernés s'appuyant sur la rotation de la Terre autour du Soleil, ou sur la rotation de la Terre sur elle-même ou sur les étoiles fixes, sont en rotation angulaire les uns par rapport aux autres, il est nécessaire de s'intéresser à la composition des vitesses angulaires.
Composition des vitesses angulaires
Les mesures d'une vitesse angulaire exprimée dans deux référentiels différents 1 et 2, identifiées par les indices /1 et /2, vérifient la "relation de Chasles" :
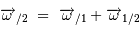
En considérant des mouvements de rotation coplanaires, l'égalité pour
les périodes devient :
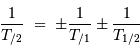
Les signes  dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
Sidéral versus synodique
Dans les cas des référentiels terrestre tournant et sidéral, la rotation propre et la révolution étant le plus souvent sur des axes parallèles et dans le même sens, on a :
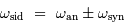
et donc :
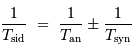
le signe 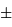 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
Par exemple, on retrouve la relation entre le jour synodique moyen (temps qui sépare deux passages du Soleil au méridien) et le jour sidéral (temps pour que la Terre fasse un tour exact sur elle-même):
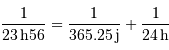
Ces 4 minutes de différence entre 23h56 et 24h00, en fait plutôt 3min56.3s, représente de l'ordre d'une fraction 1/365 de 24h.
Conversion
A l'aide de l'appliquette, convertir les périodes sidérales des planètes (Tsid) en périodes synodiques (Tsyn).

- Sélectionner la case C1, puis mener le calcul =1/(1-1/B1).
- Que se passe-t-il pour la Terre ? Sélectionner la case C3 et effacer le résultat.
- Pourquoi Mercure et Vénus se distinguent-elles ?
- Vers quelle période de révolution synodique tendent les planètes géantes ? Pourquoi ?
La rotation de Mercure
L'évolution de Mercure a conduit à figer ses périodes de rotation propre
et de révolution dans une résonance
de type 3:2, ce qui signifie que Mercure accomplit, dans un référentiel sidéral, 3 rotations
propres en 2 révolutions autour du Soleil.
Cette configuration particulière conduit, pour une hypothétique habitant
mercurien (hermien), à des jours valant deux années mercuriennes (voir
exercice), comme le montre
l'animation.
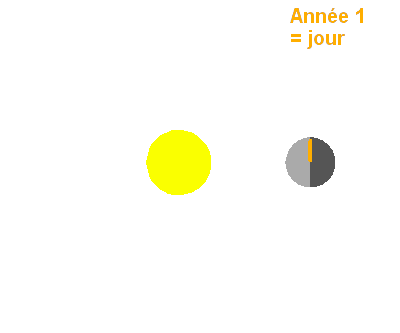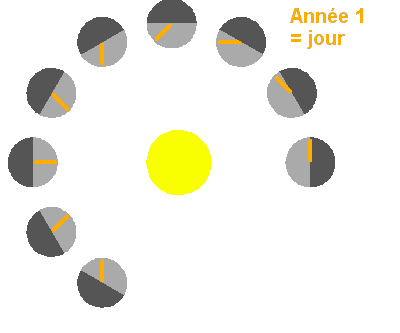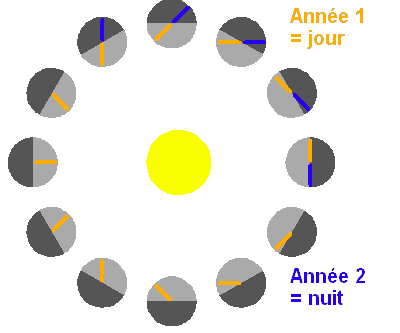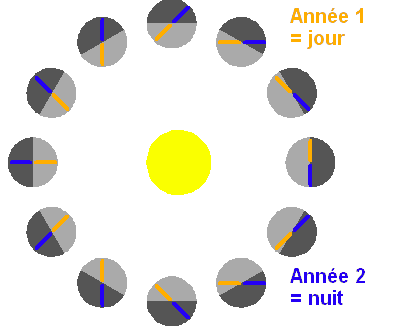
L'observateur est repéré par un tiret, jaune puis bleu. L'emploi de deux couleurs permet
de distinguer les 2 années nécessaires pour accomplir un jour sur
Mercure (ici défini entre 2 levers de Soleil).
Crédit :
ASM
 Synodique ou sidéral
Synodique ou sidéral
Difficulté : ☆
Temps : 20 min
Le tableau ci-joint donne les période de révolution sidérale des planètes du système solaire.
On veut calculer leurs périodes de révolution synodiques.
Périodes de révolution sidérale
| Planète | 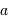 | 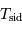 |
| UA | an |
| Mercure | 0.3871 | 0.2408 |
| Vénus | 0.7233 | 0.6152 |
| Terre | 1.0000 | 1.0000 |
| Mars | 1.5237 | 1.8808 |
| Jupiter | 5.2026 | 11.862 |
| Saturne | 9.5547 | 29.457 |
| Uranus | 19.218 | 84.020 |
| Neptune | 30.109 | 164.77 |
Question 1)
Le cas des planètes internes (Mercure, Vénus) est-il analogue à celui des planètes externes?
De la planète considérée et de la Terre,
qui double qui ?
Question 2)
Calculer les révolutions synodiques.
Question 3)
Pourquoi les périodes synodiques ci-dessus calculées tendent-elles vers un an lorsque l'on s'éloigne dans le système solaire ?
 Ils tournent
Ils tournent
Difficulté : ☆☆☆
Temps : 20 min
Question 1)
En quelle durée le Soleil parcourt-il son diamètre, du fait de la rotation diurne ?
Convertir l'unité angulaire en minute de temps
Question 2)
En quelle durée la Lune parcourt-elle son diamètre ?
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Question 3)
Déterminer la durée moyenne d'une éclipse, entre les premier et dernier
contacts ? La période de révolution synodique de la Lune est de 29.5 j ; les premier et dernier contacts correspondent aux tout début et toute fin de l'éclipse (situation 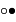 et
et  ).
).
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du
dernier contact.
Montrer que le fait de considérer la révolution synodique de la Lune
fige le mouvement du Soleil.
 Rotation de Mercure
Rotation de Mercure
Difficulté : ☆☆
Temps : 30 min
Question 1)
Déterminer la période sidérale de rotation, avec comme unité l'année hermienne
sidérale.
La question est peut être trop simple.
Question 2)
Définir les référentiels d'étude, et l'entraînement angulaire de l'un
par rapport à l'autre. Montrer alors que le jour hermien vaut 2 années sidérales.
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
 Le cas de la Lune
Le cas de la Lune
Difficulté : ☆☆
Temps : 20 min
La période de révolution synodique de la Lune, durée s'écoulant entre deux nouvelles lunes, vaut 29 j 12 h 44 min.
Question 1)
Calculer la période de révolution sidérale de la Lune.
[2 points]
Quelle rotation distingue les descriptions sidérale et synodique ?
Question 2)
Déterminer l'intervalle de temps moyen entre 2 passages consécutifs de la Lune au méridien.
[2 points]
La Lune n'est ni le Soleil, autour duquel la Terre tourne, ni les étoiles, considérées comme lointaines et fixes.
Hauteur
La coordonnée locale 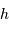 , la hauteur d'un astre, nous renseigne si un astre est levé
, la hauteur d'un astre, nous renseigne si un astre est levé
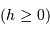 . L'angle horaire
. L'angle horaire 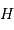 nous renseigne sur sa position par rapport au méridien (passage au méridien à
nous renseigne sur sa position par rapport au méridien (passage au méridien à 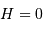 ).
).
Le tracé de 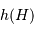 est utile pour estimer les conditions d'observations.
est utile pour estimer les conditions d'observations.
Hauteur, fonction de l'angle horaire
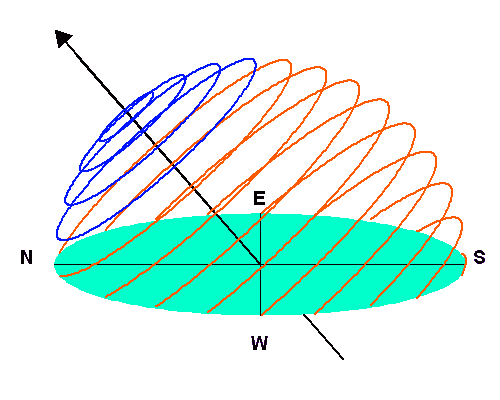
Lignes iso-déclinaison : les trajectoires
circumpolaires apparaissent en bleu.
Crédit :
ASM
Hauteur, fonction de l'angle horaire
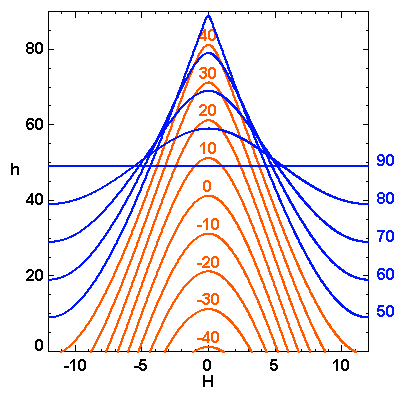
Tracé, pour la latitude
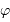
de Paris, de la hauteur
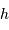
d'un astre, en fonction de l'angle horaire
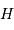
. En bleu : les astres toujours visibles, ou
circumpolaires,
de déclinaison
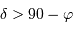
; en rouge, ceux de déclinaison dans l'intervalle
![[\varphi-90,\ 90-\varphi]](../pages_referentiels/equations_pointer/equation10.png)
, plus ou moins visibles selon l'angle horaire.
L'étoile polaire, quasi-immobile et de déclinaison proche de
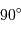
, garde bien sûr une hauteur quasi constante.
Crédit :
ASM
Visibilité
La hauteur 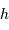 détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).
détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).
Cela dépend de l'ascension droite.
Les éphémérides et logiciels de l'IMCCE permettent de calculer positions, visibilités...
Mercure, Vénus
Les objets internes du système solaire, Mercure et Vénus, mais aussi tout petit corps de périhélie inférieur à 1 UA, ne peuvent être visibles toute la nuit (le contraire signifierait que la Terre se situe entre eux et le Soleil, ce qui est contradictoire), ce qui réduit leur durée d'observation.
Ainsi, le coucher de Mercure
suit de peu celui du Soleil.

Photomontage réalisé à partir de plusieurs images de Mercure sur l'horizon ouest, réalisées quotidiennement pendant 3 semaines, le soleil étant à une élévation de -10 degrés. Un seul fond d'image a été représenté.
Crédit :
Juan Carlos Casado
Le temps des étoiles
Comment savoir si une étoile est visible ou non, et comment la pointer, càd diriger le télescope vers elle ? Cela dépend de ses coordonnées (ascension droite et déclinaison), mais aussi du lieu, de la date et de l'heure d'observation,
comme cela a été montré aux pages traitant des
coordonnées et du temps sidéral.
Observation
Observer un astre dans les meilleures conditions, c'est l'observer lorsqu'il passe au méridien à minuit, et donc lorsque son ascension droite vaut le temps sidéral de référence (Greenwich) à minuit.
Un paramètre couramment mesuré est la masse d'air, qui n'est pas une masse mais rend compte de l'épaisseur d'atmosphère traversée. C'est la tangente de la distance zénithale, distance angulaire séparant le zénith de l'altitude de l'objet.
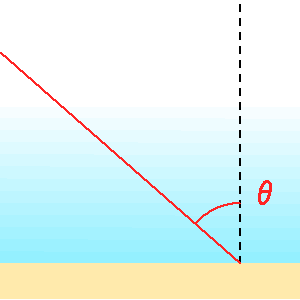
La masse d'air croît avec l'angle
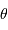
comme
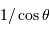
.
Crédit :
ASM
 Planète, astre errant
Planète, astre errant
Difficulté : ☆
Temps : 20 min
Question 1)
Aller rechercher les coordonnées des planètes Vénus, Mars, Jupiter et Saturne sur le site de l'Institut de Mécanique Céleste (CNRS, Observatoire de Paris). Choisir l'objet, la date, et laisser de côté le reste des informations demandées.
Question 2)
Déterminer, pour 20h00 ce soir (heure locale), le temps sidéral (pour un observatoire de votre choix), à l'aide des données de site de l'Institut de Mécanique Céleste.
Ne pas oublier de passer d'abord en temps universel.
Question 3)
Quelles planètes seront visibles (s'il fait beau) ?
Essayer de définir un critère simple de visibilité.
La planète doit être levée en début de soirée.
 Latitude / déclinaison
Latitude / déclinaison
Difficulté : ☆☆
Temps : 15min
Pour une bonne qualité d'observations, on souhaite qu'une cible stellaire étudiée culmine à une hauteur supérieure à 60 deg. Quelle contrainte cela pose-t-il sur la cible, fonction de la latitude 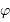 du lieu d'observation ?
du lieu d'observation ?
Question 1)
Interpréter le terme culmine.
Question 2)
Quelle contrainte cela pose-t-il sur la cible, fonction de la latitude du lieu d'observation ?
 Quand observer ?
Quand observer ?
Difficulté : ☆☆☆
Temps : 40 min
Un programme d'observation à l'Observatoire de Paris, sur le campus de Meudon, comprend les cibles stellaires ci-jointes :
Etoiles doubles
| nom | 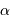 | 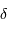 | sép. | 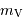 | remarque |
| (h, min) | ( | (") | | |
 Cas Cas | 00 49.1 | 57 49 | 12.2 | 3.4, 7.5 | |
 Ari Ari | 01 53.5 | 19 18 | 7.8 | 4.8, 4.8 | |
 Tau Tau | 04 22.6 | 25 38 | 19.4 | 5.5, 7.6 | |
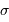 Ori Ori | 05 38.7 | -02 37 | 12.9,43 | 4,7,7.5 | quadruple en fait |
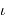 Cnc Cnc | 08 46.7 | 28 45 | 30.7 | 4.4, 6.5 | |
| 38 Lyn | 09 18.8 | 36 48 | 2.7 | 3.9, 6.6 | |
Question 1)
Vers quelle date va-t-on pouvoir observer dans la même nuit chacune de ces cibles, dans des conditions optimales, en première partie de nuit vers 22h00 heure locale?
[2 points]
Question 2)
On souhaite passer 1/2 h par cible.
Dans quel ordre les cibles devront-elles être observées ?
[1 points]
Question 3)
Pour éviter un premier quartier de Lune et tester une webcam sur la cible
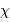 Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que
Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que 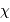 Tau culminait ?
Tau culminait ?
[1 points]
Ces pages permettent de faire le lien entre 2 étapes caractéristiques de la démarche scientifique : dans un cadre donné (p.ex. lié à la Terre entraînée autour du Soleil) mener des observations ou rendre compte de phénomènes ; puis énoncer ou valider une loi physique dans un cadre général (p.ex. dans le référentiel héliocentrique).
Les points techniques associés aux changements de référentiel ne doivent pas rebuter ; ce ne sont que des points techniques. Il existe d'ailleurs de nombreux outils qui permettent de se faciliter la tâche. Voir par exemple le serveur d'éphémérides de l'ESO (par exemple pour les étoiles), ou bien celui de l'IMCCE (par exemple pour les objets du système solaire).
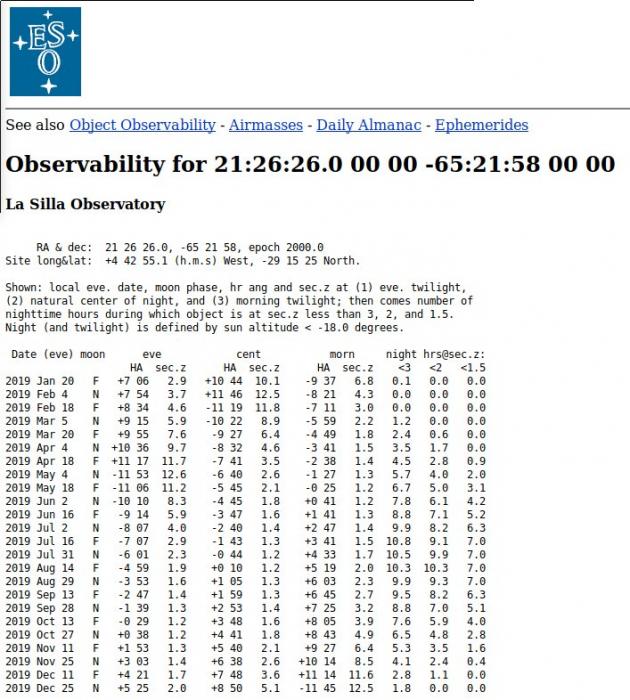
Éphémérides d'été de l'étoile HD 203608 à la Silla.
Crédit :
ESO
- Question 1
Aide :
Convertir l'unité angulaire en minute de temps
Solution :
On peut arriver au résultat de 2 façons différentes.
Soit calculer la vitesse angulaire du soleil (360 degrés en 24 h,
15 degrés à l'heure), et donc un parcours de 0.5 deg prend 2 minutes.
Soit, directement, convertir le diamètre angulaire en diamètre horaire :
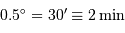 .
.
- Question 2
Aide :
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Aide :
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Solution :
Comme la durée trouvée pour le Soleil est très courte devant la période
de révolution synodique de la Lune (29.5 j), alors que la Lune présente
le même diamètre angulaire que le Soleil, on peut négliger son mouvement.
Il s'ensuit que la durée cherchée est sensiblement
la même pour la Lune que pour le Soleil.
- Question 3
Aide :
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du
dernier contact.
Aide :
Montrer que le fait de considérer la révolution synodique de la Lune
fige le mouvement du Soleil.
Solution :
Pour "doubler" totalement le soleil, la lune doit
passer de la configuration  à la configuration
à la configuration
 , càd parcourir 2 diamètres, soit 1 deg.
, càd parcourir 2 diamètres, soit 1 deg.
Ceci représente 1/360ème de la période de révolution synodique (29.5 j),
soit 0.082 j, càd environ 2 heures.
- Question 1
Aide :
La question est peut être trop simple.
Solution :
Si l'année hermienne vaut 1, le jour sidéral vaut 2/3, d'après l'énoncé, qui annonce 3 jours hermiens = 2 révolutions.
- Question 2
Aide :
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
Solution :
En unités d'année hermienne sidérale, la période de rotation propre est 2/3, et la période d'entraînement du référentiel hermien par rapport aux étoiles est 1. La relation de cours, vue avec une période synodique, s'écrit ici avec la période hermienne cherchée :
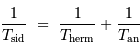
Avec 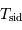 la rotation hermienne sidérale,
la rotation hermienne sidérale,
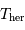 Avec
Avec 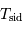 la période hermienne sidérale, la rotation hermienne,
et
la période hermienne sidérale, la rotation hermienne,
et 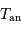 l'année hermienne sidérale.
l'année hermienne sidérale.
Donc, dans le système d'unité choisi :
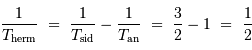
On en conclut que le jour hermien dure 2 années, comme l'illustre
l'animation.
- Question 1
Solution :
Impossible de donner une solution dynamique.
Mais vous trouverez la réponse sur le site de l'IMCCE, par exemple à l'entrée
Observations des planètes, en choisissant l'objet et la date.
Exemple de solution, au jour où cet exercice a été rédigé : la position de Mars est de 10h37 en ascension droite, et 9°55 en déclinaison.

Position de Mars.
Crédit :
IMCCE; DULU
- Question 2
Aide :
Ne pas oublier de passer d'abord en temps universel.
Solution :
Impossible de donner une solution dynamique.
Mais vous trouverez la réponse sur le site de l'IMCCE, à l'entrée
Observations des planètes, en choisissant l'objet, la date, et en précisant le lieu d'observation.
Exemple de solution, au jour où cet exercice a été rédigé : à Nançay, le temps sidéral local de Mars est de 8h01.

Temps sidéral local pour Mars.
Crédit :
IMCCE; DULU
- Question 3
Aide :
Essayer de définir un critère simple de visibilité.
Aide :
La planète doit être levée en début de soirée.
Solution :
Impossible de donner une solution en temps réel.
Mais vous trouverez la réponse sur le site de l'IMCCE, à l'entrée
Visibilité des astres, en choisissant l'objet, la date, et en précisant le lieu d'observation.
Exemple de solution, au jour où cet exercice a été rédigé : Mars se couche vers 18h45 TU, soit 20h45 en heure locale, et n'est donc pas observable cette nuit.
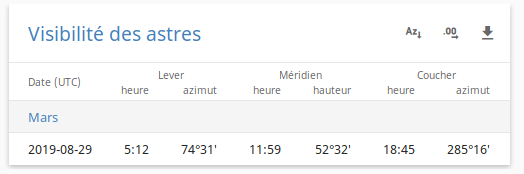
Lever et coucher de Mars.
Crédit :
IMCCE; DULU

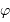 ,
les équations de passage des
,
les équations de passage des 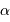 , déclinaison
, déclinaison 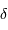 ) vers les
) vers les 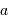 , hauteur
, hauteur 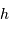 ) s'expriment par :
) s'expriment par :
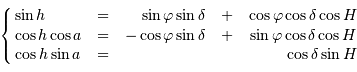
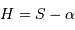 l'angle horaire,
l'angle horaire, 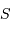 étant le temps sidéral.
étant le temps sidéral.
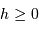 (astre au dessus de l'horizon), et en pratique
(astre au dessus de l'horizon), et en pratique 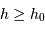 , la limite dépendant des contraintes d'observation.
, la limite dépendant des contraintes d'observation.
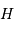 , et donc
, et donc 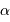 , sont estimées en
, sont estimées en 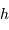 maximale, est atteint pour
maximale, est atteint pour 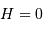 , càd
, càd 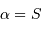 .
.
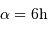 et déclinaison nulle à peu près toute la nuit (rappel :
et déclinaison nulle à peu près toute la nuit (rappel : 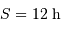 à l'équinoxe de printemps).
à l'équinoxe de printemps).
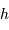 est positive, ce qui signifie :
est positive, ce qui signifie :
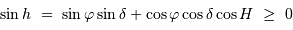
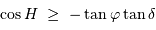
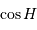 peut-il varier ?
peut-il varier ?
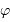 moyenne, un diagramme avec les étoiles circumpolaires (une étoile
moyenne, un diagramme avec les étoiles circumpolaires (une étoile 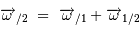
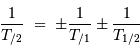
 dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
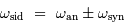
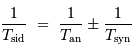
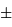 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
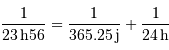

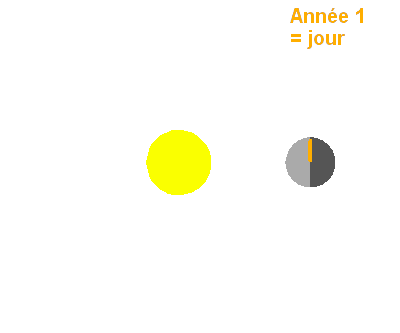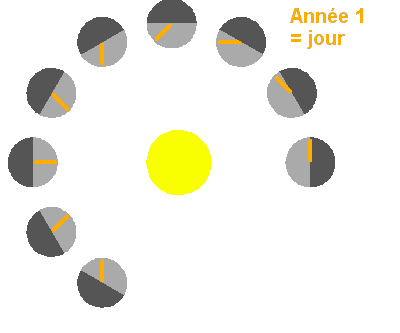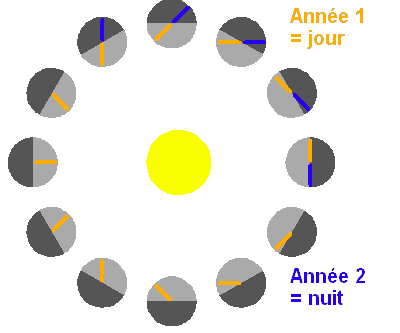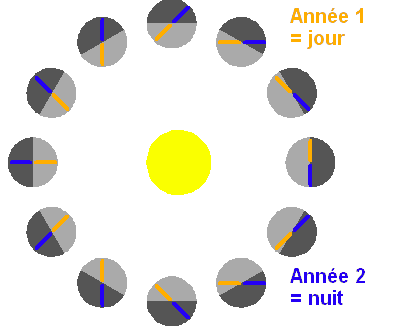
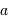
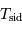
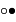 et
et  ).
).
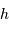 , la hauteur d'un astre, nous renseigne si un
, la hauteur d'un astre, nous renseigne si un 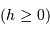 . L'angle horaire
. L'angle horaire 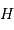 nous renseigne sur sa position par rapport au méridien (passage au méridien à
nous renseigne sur sa position par rapport au méridien (passage au méridien à 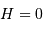 ).
).
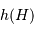


 de Paris, de la hauteur
de Paris, de la hauteur 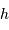 d'un astre, en fonction de l'angle horaire
d'un astre, en fonction de l'angle horaire 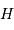 . En bleu : les astres toujours visibles, ou
. En bleu : les astres toujours visibles, ou 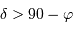 ; en rouge, ceux de déclinaison dans l'intervalle
; en rouge, ceux de déclinaison dans l'intervalle ![[\varphi-90,\ 90-\varphi]](../pages_referentiels/equations_pointer/equation10.png) , plus ou moins visibles selon l'angle horaire.
L'étoile polaire, quasi-immobile et de déclinaison proche de
, plus ou moins visibles selon l'angle horaire.
L'étoile polaire, quasi-immobile et de déclinaison proche de  , garde bien sûr une hauteur quasi constante.
, garde bien sûr une hauteur quasi constante.
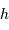 détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).
détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).


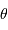 comme
comme 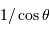 .
.
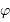 du lieu d'observation ?
du lieu d'observation ?
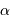
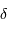
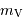
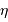 Cas
Cas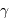 Ari
Ari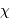 Tau
Tau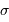 Ori
Ori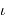 Cnc
Cnc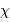 Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que
Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que 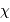 Tau culminait ?
Tau culminait ?

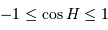 , l'inégalité précédente n'a pas de solution si
, l'inégalité précédente n'a pas de solution si 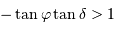 . Le cas limite est donc :
. Le cas limite est donc :
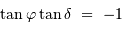
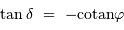
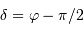 , et en tenant compte de l'inégalité, il n'y a aucune solution si
, et en tenant compte de l'inégalité, il n'y a aucune solution si
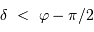
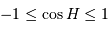 , l'inégalité précédente admet toujours une solution si
, l'inégalité précédente admet toujours une solution si 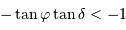 . Le cas limite est donc :
. Le cas limite est donc :
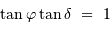
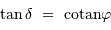
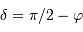 , et en tenant compte de l'inégalité, il y a toujours une solution si :
, et en tenant compte de l'inégalité, il y a toujours une solution si :
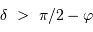
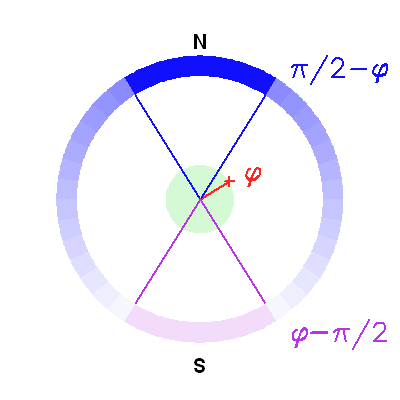
 dans la région en violet.
dans la région en violet.
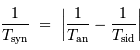
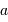
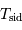
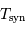
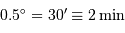 .
.
 à la configuration
à la configuration
 , càd parcourir 2 diamètres, soit 1 deg.
, càd parcourir 2 diamètres, soit 1 deg.
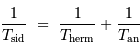
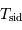 la rotation hermienne sidérale,
la rotation hermienne sidérale,
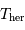 Avec
Avec 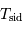 la période hermienne sidérale, la rotation hermienne,
et
la période hermienne sidérale, la rotation hermienne,
et 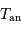 l'année hermienne sidérale.
l'année hermienne sidérale.