
 Observabilité
Observabilité
Difficulté : ☆
Temps : 5 min
Question 1)
Comment se révèle à l'observation une étoile double spectroscopique dans le cas où 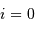 ?
?
Solution
Lorsque l'inclinaison du plan de l'orbite par rapport à la ligne de visée est nulle, les composantes radiales des vitesses orbitales sont nulles et les raies des deux étoiles se superposent... Mais si les deux étoiles sont de type spectral différent, ce qui est le cas le plus général, on verra dans le spectre des familles de raies correspondant à deux températures superficielles différentes, témoignant de la présence de deux objets distincts.

 Résolution spectrale
Résolution spectrale
Difficulté : ☆☆
Temps : 20 min
On cherche à analyse un spectre d'étoile spectroscopique double, enregistré avec une résolution dans le domaine visible 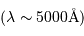 de l'ordre de
de l'ordre de 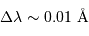 .
.
Question 1)
Quelle limitation cela impose-t-il sur les vitesses radiales que l'on peut effectivement mesurer ?
AideSolution
Voir le cours sur l'effet Doppler issues de mesures spectrométriques.
La mesure en vitesse est limitée par la résolution
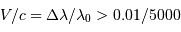
soit la valeur limite  .
.
Question 2)
Observer des grandes vitesses orbitales favorise-t-il ou non les systèmes serrés ?
AideSolution
La 3eme loi de Kepler, reliant la vitesse 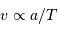 au demi-grand axe s'exprime :
au demi-grand axe s'exprime :
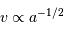
Dans le cas d'un binaire spectroscopique, le système double n'est pas résolu en ses deux composantes, et les deux étoiles entrent dans la fente du même spectrographe, ce qui implique une proximité spatiale et donc une limitation à des périodes orbitales courtes, et des vitesses élevées.

 Inclinaison de l'orbite
Inclinaison de l'orbite
Difficulté : ☆
Temps : 10 min
Question 1)
Comment peut-on vérifier que l'hypothèse 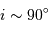 est vraie ou non ?
est vraie ou non ?
Solution
Les binaires spectroscopiques étant des couples serrés, si l'inclinaison est proche de 90°, la binaire est forcément aussi à éclipse. Ce qui se vérifie aisément par l'observation.
Question 2)
Quand l'inclinaison est inconnue, peut-on obtenir des limites inférieures ou supérieures pour les masses des deux composantes ?
Solution
D'après les expressions de la page masses des composantes , la masse étant inversement proportionnelle à 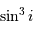 , on obtient bien une limite inférieure pour la masse de chaque composante.
, on obtient bien une limite inférieure pour la masse de chaque composante.

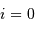 ?
?