Cas circulaire
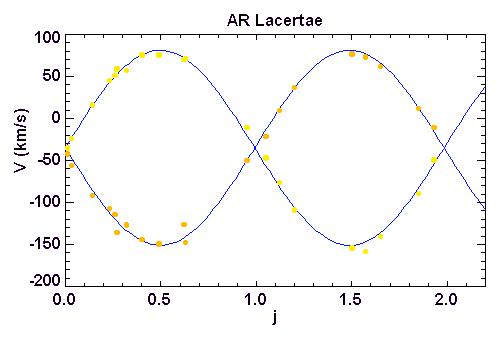
La situation la plus simple est celle où l'orbite est circulaire et vue par la tranche, soit 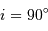 (le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse
(le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse 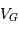 de leur barycentre, avec une même période
de leur barycentre, avec une même période 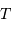 .
.
Chacune des étoiles A et B étant animée d'un mouvement circulaire et uniforme, de période 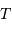 autour de G, les vitesses
autour de G, les vitesses 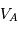 et
et 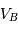 sont liées aux distances
sont liées aux distances 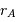 et
et 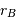 par les relations :
par les relations :
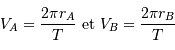
Masses
Par définition du centre de masse : 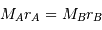 . On obtient alors le rapport des masses :
. On obtient alors le rapport des masses :
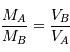
qui est donné par le rapport des amplitudes des deux courbes. D'autre part, d'après la troisième loi de Kepler, on a :
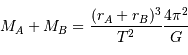
On obtient :
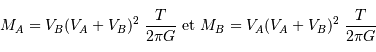
Si l'inclinaison  est différente de
est différente de 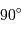 , l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur
, l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur 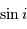
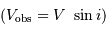 .
.
Dans les équations précédentes, 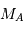 est donc remplacé par
est donc remplacé par 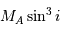 (respectivement
(respectivement 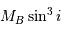 ).
).
Orbite elliptique
Si l'orbite n'est pas circulaire mais elliptique avec une excentricité 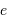 non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
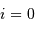 ?
?
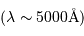 de l'ordre de
de l'ordre de 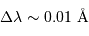 .
.
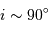 est vraie ou non ?
est vraie ou non ?
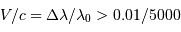
 .
.
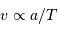 au demi-grand axe s'exprime :
au demi-grand axe s'exprime :
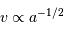
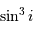 , on obtient bien une limite inférieure pour la masse de chaque composante.
, on obtient bien une limite inférieure pour la masse de chaque composante.