Soleil Terre Lune Phénomènes
Auteur: Patrick Rocher
- Introduction
- Les saisons
- Introduction
- Définition des saisons astronomiques
- Introduction
- L'orbite de la Terre autour du Soleil
- La rotation de la Terre et l'équateur terrestre
- La ligne des équinoxes et la ligne des solstices
- Les équinoxes
- Exercice
- La durée des jours et des nuits
- Trajectoires apparentes du Soleil au début des différentes saisons
- Conclusion
- Les dates des saisons
- Introduction
- La révolution tropique
- Exercice
- Les dates des saisons dans les différents calendriers
- Les dates des quatre saisons
- Conclusion
- La durée des différentes saisons
- Introduction
- La longueur des saisons
- L'évolution de la longueur des saisons
- Conclusion
- Historique : saisons
- Introduction
- Historique: La précession des équinoxes et la longueur de l'année tropique
- Historique: La longueur des saisons
- Historique: Le nombre des saisons et le climat
- Historique: Trois saisons : en Égypte ancienne
- Historique: Quatre saisons décalées : en Chine
- Historique: Cinq saisons : en Australie
- Historique: Six saisons : en Inde
- Historique: Plus de six saisons
- Conclusion
- Conclusion
- Les mouvements de la Terre et de la Lune
- Introduction
- Présentation historique
- Introduction
- Les représentations mythologiques
- Mouvement de la Terre
- Introduction
- Mouvement de la Terre autour du Soleil
- En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre
- En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre-2
- Exercice
- Mouvement orbital de la Lune
- Introduction
- La mouvement de la Lune autour de la Terre
- En savoir plus: La définition des éléments elliptiques
- En savoir plus: La définition des éléments elliptiques-2
- En savoir plus: La définition des éléments elliptiques-3
- Mouvement de la Lune et périodes de révolution
- Introduction
- Périodes de révolutions de la Lune
- En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire
- En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire-2
- En savoir plus: Les variations des éléments elliptiques de la Lune
- En savoir plus: Les variations des éléments elliptiques de la Lune-2
- Les phases de la Lune
- Introduction
- Les phases de la Lune-1
- Les phases de la Lune-2
- Les phases de la Lune-3
- En savoir plus: La lunaison moyenne, le mois lunaire
- En savoir plus: La lunaison vraie
- Exercice
- Les éclipses de Soleil
- Introduction
- Les différents types d'éclipses
- Introduction
- Dimensions et distances des corps
- Le cône d'ombre et le cône de pénombre
- Les différents types d'éclipses du soleil
- Les éclipses non centrales
- Les éclipses centrales
- Les éclipses totales
- Les éclipses totales-2
- Les éclipses totales non centrales
- Les éclipses annulaires
- Les éclipses annulaires-2
- Les éclipses annulaires non centrales
- Les éclipses mixtes et les éclipses partielles
- Exercice
- La géométrie des éclipses de Soleil
- Introduction
- Caractéristiques des cônes d'ombre et de pénombre
- Caractéristiques des cônes d'ombre et de pénombre-2
- En savoir plus: Le calcul exact des vitesses : la vitesse de l'ombre à la surface terrestre
- En savoir plus: Le calcul exact des vitesses : combinaison des vitesses
- En savoir plus: Le calcul des rayons de l'ombre et de la pénombre
- En savoir plus: Le calcul des rayons de l'ombre et de la pénombre-2
- Magnitude ou grandeur d'une éclipse de Soleil
- Degré d'obscuration d'une éclipse
- Détermination des types d'éclipses en fonction des positions orbitales
- Introduction
- Diamètres apparents
- Positions orbitales
- Types d'éclipses en fonction des distances des corps
- Types d'éclipses en fonction des distances des corps-2
- Circonstances générales et cartes des éclipses
- Introduction
- Circonstances générales
- En savoir plus: Circonstances générales de l'éclipse des 10 et 11 juin 2002
- Les cartes d'éclipses
- En savoir plus: Exemple de carte générale en projection stéréographique
- En savoir plus: Exemple de carte en projection orthographique
- En savoir plus: Exemple de carte locale
- En savoir plus: Les différentes projections
- Circonstances locales des éclipses
- Introduction
- Circonstances locales éclipses totales
- Circonstances locales éclipses annulaires
- Circonstances locales éclipses partielles
- Circonstances locales angles au pole et au zenith
- Circonstances locales-5
- En savoir plus: Définition des éléments de Bessel
- En savoir plus: Définition des éléments de Bessel-2
- En savoir plus: Définition des éléments de Bessel-3
- En savoir plus: Définition des éléments de Bessel-4
- En savoir plus: Calcul des circonstances locales
- En savoir plus: Calcul de la grandeur maximale en un lieu
- En savoir plus: Calcul des instants des contacts en un lieu
- En savoir plus: Calcul de l'angle au pôle et de l'angle au zénith
- Visibilité des éclipses de Soleil
- Introduction
- Quand ont lieu les éclipses de Soleil ?
- Introduction
- Le mouvement moyen de la ligne des noeuds
- Le mouvement moyen de la ligne des noeuds-2
- En savoir plus: Le calcul de la saison des éclipses
- En savoir plus: Le mouvement réel de la ligne des noeuds
- Le critère en latitude
- Les bornes du critère en latitude
- En savoir plus: La parallaxe solaire et la parallaxe lunaire
- En savoir plus: La démonstration du critère en latitude
- En savoir plus: Critère en latitude-3
- En savoir plus: Critère en latitude-4
- En savoir plus: Critère en latitude-5
- En savoir plus: Critère en latitude-6
- Critère en longitude
- Nombres d'éclipses de Soleil ?
- Introduction
- Nombre d'éclipses à chaque saison d'éclipses
- Nombre d'éclipses à chaque saison d'éclipses-2
- Nombre d'éclipses à chaque saison d'éclipses-3
- Nombre d'éclipses par an
- Nombre d'éclipses par an-2
- Nombre d'éclipses par an-3
- Les séries courtes d'éclipses
- Les séries courtes d'éclipses-2
- Les séries courtes d'éclipses-3
- Répartition des éclipses sur une période de 22 ans
- exercice eclipse soleil
- Canons et grandeurs des éclipses de Soleil
- Introduction
- Les canons d'éclipses de Soleil
- En savoir plus: Le canon de l'IMCCE : les théories utilisées
- En savoir plus: Le canon de l'IMCCE : les paramètres physiques
- En savoir plus: Le canon de l'IMCCE : les résultats
- Les éclipses totales les plus longues
- Les éclipses totales les plus longues-2
- Les éclipses annulaires les plus longues
- Les éclipses partielles les plus petites
- L'éclipse de 651
- L'éclipse de 1327
- Les éclipses récentes et futures
- Introduction
- Les éclipses totale entre 1998 et 2020
- Les éclipses annulaires entre 1998 et 2020
- Fréquence des éclipses centrales de Soleil en France
- Fréquence des éclipses centrales de Soleil en France-2
- Eclipses du XVI, XVII et XVIIIème siècles, visibles en France
- Eclipses du XIX et du XXème siècles visibles en France
- Eclipses du XXI siècle visibles en France
- Observation d'une éclipse de Soleil
- Introduction
- Précautions à prendre pour observer une éclipse de Soleil
- Précautions à prendre pour observer une éclipse de Soleil-2
- Précautions à prendre pour observer une éclipse de Soleil-3
- L'utilisation de filtres pour l'observation des éclipses
- L'utilisation de filtres pour l'observation des éclipses-2
- L'utilisation de filtres pour l'observation des éclipses-3
- L'utilisation de filtres pour l'observation des éclipses-4
- Les traumatismes causés par le Soleil
- Récurrences des éclipses de Soleil
- Introduction
- Les périodes de récurrences des éclipses
- Introduction
- Les périodes de récurrence
- Périodes de récurrence-2
- Périodes de récurrence-3
- Périodes de récurrence-4
- En savoir plus: Décomposition d'un réel en fractions continues
- En savoir plus: Décomposition d'un réel en fractions continues-2
- En savoir plus: Autres périodes de récurrence
- En savoir plus: Autres périodes de récurrence-2
- L'origine du nom "saros"
- L'origine du nom "saros"-2
- Nombre d'éclipses dans un saros
- Les suites longues d'éclipses
- Introduction
- Eclipses homologues et suites longues
- Eclipses homologues et suites longues-2
- Eclipses homologues et suites longues-3
- Eclipses homologues et suites longues-4
- Evolutions des éclipses homologues
- Evolutions des éclipses homologues
- En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues
- En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues-2
- Evolutions des éclipses homologues - suite
- Evolutions des éclipses homologues - suite2
- En savoir plus: Exemple de saros, exemple de suite longue
- En savoir plus: Exemple de saros-2
- Les éclipses anciennes
- Introduction
- Le ralentissement de la Terre
- Les échelles de temps
- L'usage des éclipses anciennes
- Les sources anciennes
- Les sources anciennes-2
- Exemple de la détermination du ralentissement de la rotation terrestre
- La prédiction des éclipses
- Intérêt scientifique des éclipses de Soleil
- Intérêt scientifique des éclipses de Soleil-2
- Les éclipses de Lune
- Introduction
- La géometrie des éclipses de Lune
- Introduction
- Le cône d'ombre et le cône de pénombre
- Les différents types d'éclipses de Lune
- Caractéristiques des cônes d'ombre et de pénombre
- Les effets géométriques de l'atmosphère terrestre
- Les effets lumineux de l'atmosphère terrestre
- Grandeur d'une éclipse de Lune
- Les données fournies pour une éclipse de Lune
- En savoir plus: Exemple de données
- Zones de visibilité d'une éclipse de Lune
- En savoir plus: Carte de visibilité de l'éclipse totale du 4 mai 2002
- Quand ont lieu les éclipses de Lune ?
- Introduction
- Le mouvement moyen de la ligne des noeuds
- En savoir plus: Le calcul de la saison des éclipses
- En savoir plus: Le mouvement réel de la ligne des noeuds
- Le critère en latitude
- En savoir plus: La démonstration du critère en latitude
- En savoir plus: La démonstration du critère en latitude-2
- Le critère en longitude
- Nombre d'éclipses à chaque saison d'éclipse
- Nombre d'éclipses par an
- Les séries courtes d'éclipses
- Répartition des éclipses sur une période de 22 ans
- Canons et grandeurs des éclipses de Lune
- Introduction
- Grandeurs des éclipses de Lune
- Les canons d'éclipses de Lune
- En savoir plus: Le canon de l'IMCCE
- Les éclipses totales les plus longues
- Les éclipses totales les plus grandes
- Les éclipses les plus faibles et les plus courtes
- Le Saros et les suites longues d'éclipses de Lune
- Introduction
- Nombre d'éclipses dans un Saros
- Eclipses homologues et suites longues d'éclipses de Lune
- Evolutions des éclipses homologues
- En savoir plus: Positions des éclipses d'une saison éclipse
- Evolutions des suites homologues - suite
- En savoir plus: Exemple de Saros
- Les éclipses anciennes
- Introduction
- Visibilité des éclipses anciennes à l'oeil nu
- Quelques éclipses historiques
- Rotondité de la Terre
- Le calcul de la distance Terre-Lune
- Introduction
- Par Aristarque de Samos
- En savoir plus: Une des démonstrations d'Aristarque
- Par Claude Ptolémée
- Problèmes et QCM
- Introduction
- QCM Soleil-Terre-Lune
- QCM sur les calendriers
- QCM sur les mouvements de la Terre et de la Lune
- QCM sur les saisons et les levers couchers
- QCM sur les éclipses
- QCM sur la durée des éclipses
- Exercice 1 : Marco et Polo en ULM
- Exercice 2 : Marco et Polo font du bateau
- Énoncé
- Hypothèses supplémentaires et rappels
Introduction
 Prérequis
Prérequis
 Introduction
Introduction
Auteur: P. Rocher IMCCE
Date de création: 3 mars 2005
Ce chapitre traite de trois phénomènes liés au système Terre Lune Soleil : Les saisons, les éclipses de Soleil et les éclipses de Lune.
Les saisons climatiques sont liées aux saisons astronomiques. Très tôt les hommes vont essayer de comprendre ce phénomène et vont l'associer à des configurations astronomiques particulières. Les saisons astronomiques, le calcul de leurs retours sont l'origine des calendriers solaires.
Le cours sur les éclipses ne traite que de l'aspect mécanique (céleste) des éclipses, les aspects physiques et astrophysiques ne sont pas traités. Ce cours va nous permettre de répondre aux cinq questions fondamentales suivantes : Comment ? Pourquoi ? Quand ? Où ? et Souvent ?
Le cours sur les éclipses est séparé en quatre parties, les trois premières parties portent sur les éclipses de Soleil et une dernière partie porte sur les éclipses de Lune, les sections sur les éclipses de Soleil sont donc beaucoup plus fournies que la partie sur les éclipses de Lune, en effet il y a de nombreux points communs aux deux types d'éclipses et ils ne sont pas repris dans la dernière partie, il est donc vivement conseillé de lire le cours sur les éclipses de Soleil avant le cours sur les éclipses de Lune.
 Remarque
Remarque
Ces cours comportent de nombreuses cartes d'éclipses, pour des raisons purement informatiques nous avons limité la taille donc la définition de ces images, vous trouverez des cartes et des images ayant une plus grande définition sur le site de l'IMCCE dans les rubriques éclipses. Vous y trouverez également des prédictions pour les futures éclipses de Lune et de Soleil.
Les saisons
Auteur: Patrick Rocher
Introduction
 Prérequis
Prérequis
 Introduction
Introduction
Les climats terrestres dépendent de trois facteurs principaux : un facteur astronomique lié aux mouvements de la Terre autour du Soleil et à la rotation de la Terre sur elle-même; un facteur dynamique lié au déplacement saisonnier des masses d'air et un facteur thermique lié à la réflexion de la surface terrestre et au bilan radiatif. Nous traiterons principalement du premier facteur que l'on appelle les saisons astronomiques.
Nous allons définir les quatre saisons astronomiques qui sont en phase avec les hauteurs du Soleil et les durées du jour. Cela nous amènera à définir quelques termes parfois complexes mais qui permettent de mieux comprendre comment sont définies les dates et les durées des saisons. Nous comparerons enfin différents calendriers à différentes époques et en différents lieux sur Terre. Le facteur astronomique dominant est la hauteur du Soleil au-dessus de l'horizon. En effet plus le Soleil est haut, plus la quantité de chaleur reçue par mètre carré est importante, plus il fait chaud. La durée du jour n'est pas le phénomène prédominant, ainsi au pôle le jour dure plus de six mois mais il ne fait pas chaud car la hauteur du Soleil ne dépasse jamais 23°. Il n'y a donc pas de causalité entre la durée du jour et le climat, par contre la durée du jour peut intervenir dans les phénomènes météorologiques locaux (rosée, brises de mer). Les autres facteurs climatiques prennent souvent le pas sur l'échauffement dû à la hauteur du Soleil. Ainsi en France les journées les plus chaudes sont souvent celles du mois d'août alors que le Soleil est le plus haut dans le ciel au voisinage du solstice d'été (21 juin). La fraîcheur de mois de juin est due à un phénomène météorologique, une mini mousson produite par la présence de l'Atlantique.
Résumé
Les variations de hauteur du Soleil au cours du temps et les durées variables des jours sont dues à l'inclinaison de l'axe de rotation de la Terre sur l'orbite terrestre. Au cours de sa révolution autour du Soleil, la Terre passe par des positions particulières : les équinoxes et les solstices. Les dates et les longueurs des saisons ne sont pas toujours les mêmes mais on peut les calculer et les expliquer.
Définition des saisons astronomiques
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire et définir le mouvement de la Terre autour du Soleil et sa rotation sur elle-même. Nous définirons ensuite la ligne des équinoxes et des solstices, puis nous étudierons les durées du jour et la trajectoire apparente du Soleil au début de chaque saison. Cette section donne de nombreuses définitions de termes astronomiques.
L'orbite de la Terre autour du Soleil
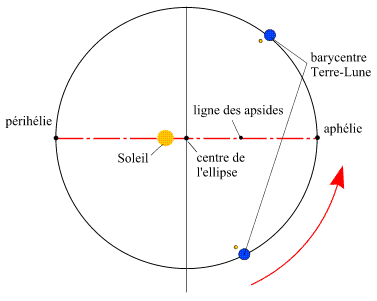
Orbite elliptique du barycentre Terre-Lune dans le plan de l'écliptique
Crédit : IMCCE/Patrick Rocher
En première approximation, le barycentre du système Terre-Lune parcourt, dans le sens direct (sens inverse des
aiguilles d'une montre), une orbite quasi elliptique et plane autour du Soleil (première loi de Kepler). Le plan de cette
orbite est appelé plan de l'écliptique. Le Soleil est situé à l'un des foyers de cette ellipse. L'excentricité de l'ellipse est tellement faible qu'elle est indécelable sur le tracé de l'orbite, le tracé ressemble à celui d'un cercle. Il est important de noter que le Soleil ne se trouve pas au centre de l'ellipse mais à l'un de ces foyers. La distance entre le barycentre Terre-Lune et le Soleil n'est donc pas constante. Il y a deux positions particulières correspondant aux valeurs extrêmes de cette distance : le périhélie (distance minimale) et l'aphélie (distance maximale). La ligne joignant ces deux positions s'appelle ligne des apsides.
La rotation de la Terre et l'équateur terrestre
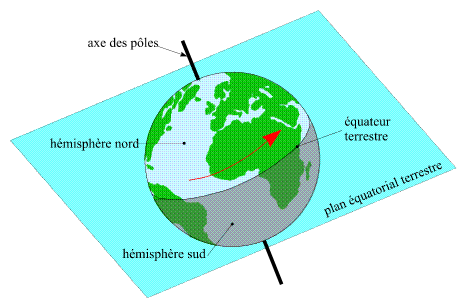
Rotation de la Terre : l'équateur terrestre
Crédit : IMCCE/Patrick Rocher
La Terre tourne sur elle-même, autour de l'axe des pôles, dans le sens direct (d'ouest en est). L'axe de rotation de la
Terre n'est pas normal au plan de l'orbite du barycentre Terre-Lune (plan de l'écliptique). Cette inclinaison, de 23° 26', est à l'origine des variations de la durée des jours et des nuits ainsi que des saisons. Le plan normal à l'axe de rotation
terrestre coupant en deux hémisphères la sphère terrestre s'appelle plan équatorial terrestre. L'intersection de ce plan
avec la Terre est l'équateur terrestre.
La ligne des équinoxes et la ligne des solstices
Comme l'axe de rotation de la Terre n'est pas normal au plan de l'écliptique, le plan équatorial terrestre n'est pas
parallèle au plan de l'écliptique. Il le coupe donc suivant une droite. Cette droite s'appelle la ligne des équinoxes.
Lorsque la direction du segment joignant le Soleil à la Terre est parallèle à celle ligne, la Terre se trouve aux équinoxes.
Il existe une autre ligne particulière, la ligne perpendiculaire, dans le plan de l'écliptique, à la ligne des équinoxes. Cette
ligne est la ligne des solstices. Lorsque la direction du segment joignant le Soleil à la Terre est parallèle à celle ligne, la Terre se trouve aux solstices.
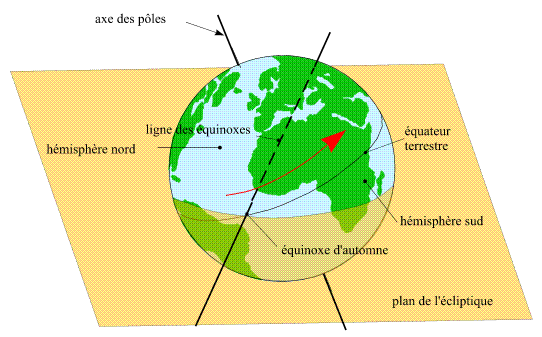
Ligne des équinoxes
Crédit : IMCCE/Patrick Rocher
Les équinoxes
Repère géocentrique équatorial
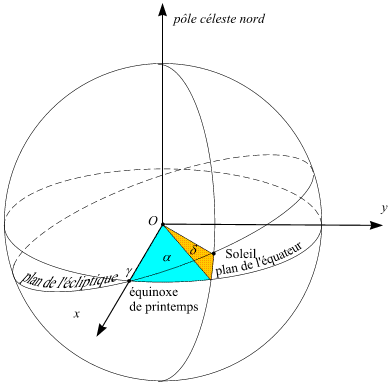
O : centre de la Terre, Oxy : plan de l'équateur, O
γ : direction de l'équinoxe de printemps, α : ascension droite, δ : déclinaison de l'astre
Crédit : IMCCE/Patrick Rocher
Vu de la Terre, dans le repère équatorial géocentrique, l'équinoxe correspondant au passage du Soleil des déclinaisons
négatives aux déclinaisons positives est appelé équinoxe de printemps (début du printemps dans l'hémisphère nord) ou
point vernal. Cette direction est, dans le plan de l'écliptique, l'origine des longitudes célestes et elle est également, dans
le plan de l'équateur, l'origine des ascensions droites.
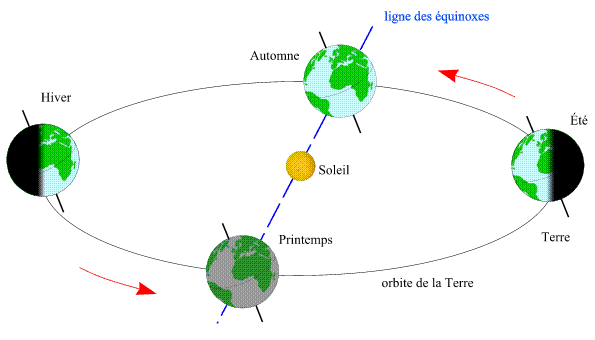
Saisons dans l'hémisphère nord
Crédit : IMCCE/Patrick Rocher
Le printemps, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 0°. L'autre équinoxe, correspondant au passage du Soleil des déclinaisons positives aux déclinaisons négatives, est appelé équinoxe d'automne (début de l'automne dans l'hémisphère nord). L'automne, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 180°.
Le solstice situé entre l'équinoxe de printemps et l'équinoxe d'automne est le solstice d'été et le solstice compris entre l'équinoxe d'automne et l'équinoxe de printemps est le solstice d'hiver. L'été, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 90°. De même, le solstice d'hiver, dans l'hémisphère nord, correspond à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 270°.
 Remarque
Remarque
Les saisons dans l'hémisphère sud sont inversées par rapport aux saisons dans l'hémisphère nord. Ainsi l'été dans l'hémisphère sud correspond à l'hiver dans l'hémisphère nord, l'hiver dans l'hémisphère sud correspond à l'été dans l'hémisphère nord, le printemps dans l'hémisphère sud correspond à l'automne dans l'hémisphère nord et l'automne dans l'hémisphère sud correspond au printemps dans l'hémisphère nord.
Exercice
 Saisons et équateur
Saisons et équateur
Question 1)
Nous venons de voir qu'il y a inversion des saisons entre l'hémisphère nord et l'hémisphère sud.
Pouvez-vous décrire en quelques lignes ce qui se passe lorsque l'on est à la limite des deux hémisphères, c'est-à-dire lorsque l'on est sur l'équateur ?
La durée des jours et des nuits
Le jour de l'équinoxe
Le jour de l'équinoxe (de printemps ou d'automne), si on néglige la réfraction atmosphérique, le terminateur de la zone de nuit sur la Terre passe par les deux pôles terrestres. Le jour de l'équinoxe, si on néglige la réfraction atmosphérique, la durée du jour est égale à la durée de la nuit pour tous les lieux de la surface terrestre. De plus, toujours en négligeant l'effet de la réfraction atmosphérique, le jour des équinoxes le Soleil se lève exactement à l'est et se couche exactement à l'ouest.
Le jour du solstice d'hiver
Le jour du solstice d'hiver, pour l'hémisphère nord, la demi-sphère définie par le terminateur de la zone de nuit
recouvre la plus grande partie de la surface de l'hémisphère nord. C'est le jour de l'année où la durée de la nuit est
maximale et la durée du jour minimale. C'est également le jour où le Soleil se lève le plus au sud-est (valeur extrême de l'amplitude ortive), passe au méridien avec une hauteur minimale et se couche le plus au sud-ouest(valeur extrême de l'amplitude occase).
Le jour du solstice d'été
Le jour du solstice d'été, pour l'hémisphère nord, la demi-sphère définie par le terminateur de la zone de nuit recouvre
la plus petite partie de la surface de l'hémisphère nord. C'est le jour de l'année où la durée de la nuit est minimale et la
durée du jour maximale. C'est également le jour où le Soleil se lève le plus au nord-est (valeur extrême de l'amplitude ortive), passe au méridien avec une
hauteur maximale et se couche le plus au nord-ouest (valeur extrême de l'amplitude occase).
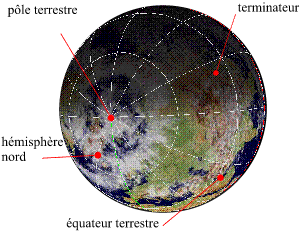
Equinoxes
Crédit : IMCCE/Patrick Rocher
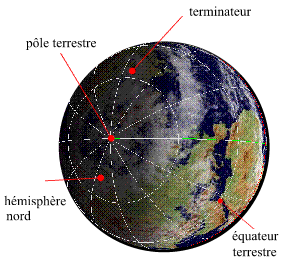
Solstice d'hiver
Crédit : IMCCE/Patrick Rocher
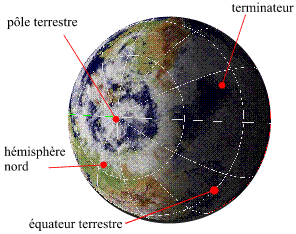
Solstice d'été
Crédit : IMCCE/Patrick Rocher
Trajectoires apparentes du Soleil au début des différentes saisons
Nous rappelons que dans l'hémisphère sud, les solstices et les équinoxes sont à l'opposé des solstices et des équinoxes de l'hémisphère nord.
La Terre tourne autour de son axe dans le sens direct (d'ouest en est). Sur la Terre cela se traduit par un mouvement apparent des étoiles et des corps du système solaire dans le sens rétrograde (d'est en ouest).
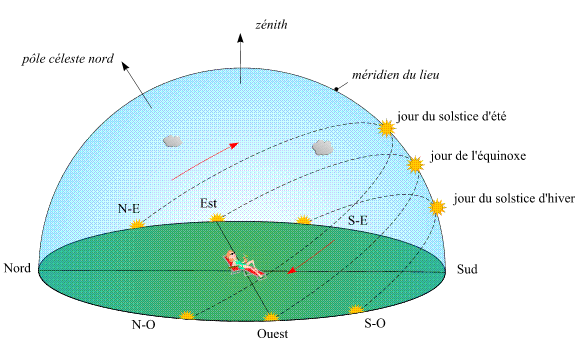
La figure illustre les trajectoires apparentes du Soleil pour chacune de ces journées en un lieu de l'hémisphère nord.
Crédit : IMCCE/Patrick Rocher
L'angle formé par la direction du lever du Soleil avec la direction de l'est porte le nom d'amplitude ortive, cette amplitude est nulle le jour des équinoxes et elle est maximale le jour des solstices.
De même l'angle formé par la direction du coucher du Soleil avec la direction de l'ouest s'appelle l'amplitude occase,
cette amplitude est nulle le jour des équinoxes et elle est maximale le jour des solstices.
 Conseils
Conseils
Il existe un moyen mnémotechnique pour se rappeler quelles amplitudes ortives ou occases correspond au coucher ou au lever d'un astre.
Les deux premières lettres des mots vous donnent la direction : OR pour ortive correspond à ORIENT donc à l'est donc au lever des astres (tous les astres se lèvent vers l'est), OC pour occase correspond à OCCIDENT donc à l'ouest donc au coucher des astres (tous les astres se couchent vers l'ouest).
Conclusion
 Conclusion
Conclusion
La Terre tourne autour du Soleil en suivant une orbite elliptique, sa vitesse sur cette orbite n'est pas constante. Les débuts des saisons astronomiques correspondent à quatre points particuliers de son orbite : les solstices et les équinoxes. Les valeurs extrêmes de la durée du jour et des positions du Soleil à son lever et à son coucher ainsi que sa hauteur correspondent aux jours des solstices.
Les dates des saisons
Introduction
 Introduction
Introduction
Cette section est entièrement consacrée aux dates des saisons, elle aborde les notions d'année tropique, d'année sidérale et de calendriers solaires.
La révolution tropique
La ligne des équinoxes n'est pas fixe. Elle est animée d'un mouvement de précession dans le sens rétrograde (50,288200" par an
actuellement). Ce mouvement appelé précession des équinoxes est lié au mouvement de l'axe de rotation de la Terre
qui décrit un cône dans le sens rétrograde en environ 26000 ans.
L’année tropique moyenne ou révolution tropique est le temps que met la Terre pour faire une révolution autour du Soleil dans un repère tournant lié à la ligne des équinoxes, c’est donc la période liée à la différence entre la longitude moyenne du Soleil et la précession des équinoxes. Cette période est indépendante de l’origine choisie. Sa valeur moyenne pour l'époque J2000 est de 365,24219052 jours (soit 365 jours 5h 48m 45,26s). L'année tropique moyenne est différente du temps moyen que met la Terre pour aller d’un équinoxe de printemps à l’autre. En effet la vitesse de la Terre sur son orbite n’est pas uniforme, elle obéit, en première approximation, à la seconde loi de Kepler, donc le temps moyen mit pour aller d’un équinoxe de printemps à l’autre n’est pas égal au temps moyen qui sépare deux équinoxes d’automne et il en est de même pour les intervalles de temps séparant les solstices d’hiver et d’été. L'année tropique moyenne est est inférieure à l'année sidérale, qui correspond à l'intervalle de temps qui sépare deux passages de la Terre dans une même direction et qui est égale à 365,2563 jours (soit 365 jours 6h 9m 6s).
Pourquoi les saisons tombent-elles toujours aux mêmes dates ?
Cela est dû à notre calendrier, le calendrier grégorien, qui est construit de manière à avoir une longueur moyenne de
l'année la plus proche possible de la révolution tropique de la Terre. Comme la révolution tropique n'a pas un nombre
entier de jour, si on prend une année calendaire de 365 jours, il y a un décalage de 0,2422 jour d'une année à l'autre
dans les dates des saisons et, au bout de quatre ans, ce décalage est presque de un jour. Pour compenser ce décalage on
a, dans un premier temps, ajouté un jour à l'année tous les quatre ans (année bissextile de 366 jours). C'est ce que
faisait le calendrier julien élaboré par Jules César en 46 avant J.-C. Mais si on ajoute un jour tous les quatre ans, la valeur moyenne de l'année calendaire est de 365,25 jours. Elle est donc un peu trop grande par rapport à l'année tropique. Donc si on se contente d'ajouter une année bissextile tous les quatre ans les saisons vont se décaler lentement par rapport au calendrier à raison de 0,0078 jour par an (11min 14s par an). Le calendrier julien suit donc mal les saisons. Il se décale d'environ 3 jours au bout de 400 ans. Pour avoir une meilleure concordance entre le calendrier et les saisons, il suffit de supprimer 3 jours sur une période de 400 ans.
C'est ce que l'on fait dans le calendrier grégorien. Comme dans le calendrier julien, on ajoute une année bissextile tous
les quatre ans (ceux dont le millésime est multiple de quatre) sauf pour les années qui sont multiples de 100 sans l'être de 400. Ainsi 1600 et 2000 sont bissextiles, mais 1700, 1800, 1900 et 2100 ne sont pas bissextiles. Cette réforme du calendrier a été effectuée par le pape Grégoire XIII en 1582. De plus, pour supprimer le décalage accumulé entre les saisons et l'ancien calendrier (calendrier julien) et ramener la date de l'équinoxe de printemps au 21 mars, l'année 1582 a été raccourcie de 10 jours, le lendemain du jeudi 4 octobre 1582 devenant le vendredi 15 octobre 1582.
Exercice
 Année tropique
Année tropique
Question 1)
Nous avons vu que la période de révolution tropique moyenne de la Terre est de : 365,24219052 jours.
Cette valeur est la combinaison du mouvement en longitude de la Terre dans un repère fixe et de la précession des équinoxes.
La longitude moyenne de la Terre pour l'époque J2000 est donnée par la formule suivante :
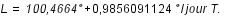
La précession des équinoxes en longitude dans le même repère est donnée par la formule :
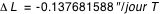
T est exprimé en jour.
A partir de ces deux formules retrouver les périodes de révolutions sidérale et tropique de la Terre pour l'époque J2000.
Les dates des saisons dans les différents calendriers
Le calcul des saisons à l'aide du programme
Le programme de calcul des dates des saisons donne ces dates dans le calendrier julien pour les dates antérieures au 5 octobre 1582 et dans le calendrier grégorien pour les dates postérieures au 15 octobre 1582. Le calendrier julien a été prolongé pour les dates antérieures au début de l'ère chrétienne (calendrier proleptique). Dans l'affichage de ces dates on utilise la notation des astronomes et non pas la notation des historiens.
La dérive des saisons dans le calendrier julien
Comme nous l'avons vu dans un paragraphe précédent, les dates des saisons se décalent dans le calendrier julien
d'environ 3 jours tous les 400 ans. On peut constater cette dérive à l'aide du programme de calcul des saisons.
| Année |
Printemps |
Eté |
Automne |
Hiver |
| 0 |
22 mars |
24 juin |
25 septembre |
22 décembre |
| -1000 |
30mars |
2 juillet |
2 octobre |
29 décembre |
| -2000 |
7 avril |
10 juillet |
9 octobre |
6 janvier |
| -3000 |
14 avril |
18 juillet |
15 octobre |
13 janvier |
| -4000 |
22 avril |
25 juillet |
22 octobre |
20 janvier |
Dérive de la date des saisons dans le calendrier julien
Les dates des saisons dans le calendrier grégorien
Nous l'avons vu, le calendrier grégorien est conçu pour éviter le décalage et la dérive des dates des saisons que nous avons
constaté dans le calendrier julien. Les dates des saisons restent donc toujours au voisinage des mêmes dates dans le
calendrier grégorien. L'utilisation des années bissextiles fait osciller l'instant des saisons sur trois et, exceptionnellement,
quatre jours. Il ne faut pas confondre ces oscillations de la date des saisons autour de valeurs moyennes avec une dérive du calendrier.
Les dates des quatre saisons
- Les dates de l'équinoxe de printemps : Aux XIXe et XXe siècles, l'équinoxe de printemps tombe toujours le 20 ou le 21 mars. Dans le passé il est tombé
le 19 mars en 1652, 1656, 1660, 1664, 1668, 1672, 1676, 1680, 1684, 1685, 1688, 1689, 1692, 1693, 1696,
1697, 1780, 1784, 1788, 1792 et 1796.
Il tombera de nouveau le 19 mars en 2044.
- Les dates du solstice d'été : Dans le calendrier grégorien, le solstice d'été peut tomber les 19, 20, 21 ou 22 juin. En général, il tombe le 21 juin. Il
est tombé un 20 juin en 1896 et tombera de nouveau à cette date en 2008. Il est tombé un 22 juin en 1975 et tombera
de nouveau à cette date en 2203, 2207, 2211 et 2215 puis en 2302. Le solstice d'été tombera un 19 juin en 2488 (et
ce sera la première fois depuis la création du calendrier grégorien) puis en 2492 et 2496.
- Les dates de l'équinoxe d'automne : Dans le calendrier grégorien, l'équinoxe d'automne peut tomber le 21, 22, 23 ou 24 septembre. Il tombe en général le
22 ou le 23 septembre. Il tombera le 21 septembre en 2092 et ce sera la première fois depuis la création du calendrier
grégorien. Cela se reproduira en 2096, puis en 2464, 2468, 2472, 2476, 2480, 2484, 2488, 2492, 2493, 2496 et
2497. Il est tombé un 24 septembre en 1803, 1807, 1903, 1907, 1911, 1915, 1919, 1923, 1927 et 1931, il tombera
de nouveau à cette date en 2303.
- Les dates du solstice d'hiver : Dans le calendrier grégorien le solstice d'hiver peut tomber le 20, 21,22 ou 23 décembre. Il tombe en général le 21 ou
le 22 décembre. Il est tombé un 23 décembre en 1903 et tombera de nouveau à cette date en 2303, 2307, 2311 et
2315. Il est tombé un 20 décembre en 1664, 1668, 1672, 1676, 1680, 1684, 1688, 1692, 1696 et 1697 et tombera
de nouveau à cette date en 2080, 2084, 2088, 2092, 2096, 2488, 2492 et 2496.
Ces dates peuvent être vérifiées à l'aide du programme de calcul des saisons.
Conclusion
 Conclusion
Conclusion
Les dates des saisons sont fixes dans un calendrier, c'est-à-dire ne dérivent pas avec le temps, lorsque la durée moyenne de l'année calendaire est proche de la révolution tropique moyenne de la Terre. Ces calendriers portent le nom de calendrier solaire. Notre calendrier actuel, le calendrier grégorien est un calendrier solaire.
La durée des différentes saisons
Introduction
 Introduction
Introduction
Cette section traite de la longueur des saisons et de l'évolution de la longueur des saisons en fonction du temps.
La longueur des saisons
Il suffit de consulter un calendrier pour vérifier que les longueurs des différentes saisons ne sont pas égales. Par exemple durant l'année 1998, l'hiver a duré 89 jours, le printemps 92 jours 18 heures, l'été 93 jours 15 heures et l'automne 89 jours 21 heures.
Cette variation des longueurs des saisons provient du fait que la vitesse du barycentre Terre-Lune sur son orbite autour du Soleil n'est pas un mouvement uniforme. C'est une conséquence immédiate de la seconde loi de Kepler. La vitesse orbitale n'est pas constante. Lorsque le barycentre Terre-Lune est au plus près du Soleil (à son périhélie) sa vitesse est maximale et lorsque le barycentre Terre-Lune est au plus loin du Soleil (à son aphélie) sa vitesse est minimale. Or actuellement le barycentre Terre-Lune passe au périhélie début janvier et à l'aphélie début juillet. Donc la Terre est plus rapide sur son orbite en janvier et l'hiver est la saison la plus courte, de même elle est la plus lente en juillet et l'été est la saison la plus longue.
Durée des saisons
| Année |
Durée de l'hiver |
Durée du printemps |
Durée de l'été |
Durée de l'automne |
Date du passage au périhélie |
Date du passage à l'aphélie |
| 130 avant J. -C. |
90 jours 5h 39m 58s |
94 jours 0h 21m 33s |
92 jours 8h 24m 42s |
88 jours 15h 25m 7s |
1 décembre à 5h 43m 23s |
2 juin à 21h 11m 54s |
| 2004 |
88 jours 23h 44m 49s |
92 jours 18h 8m 14s |
93 jours 15h 32m 57s |
89 jours 20h 11m 46s |
4 janvier à 17h 41m 59s |
5 juillet à 10h 53m 28s |
Comparaison de la durée des saisons entre l'an 130 avant J.-C. et l'an 2004.
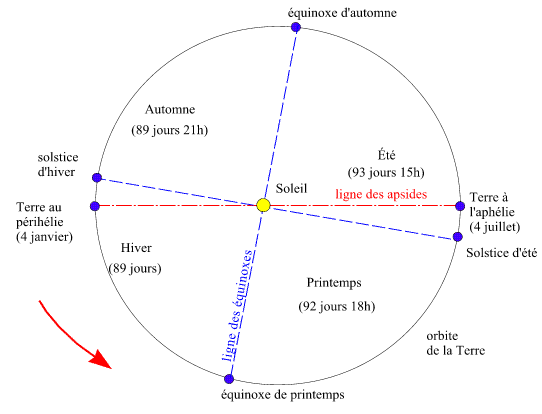
Durée des saisons pour l'année 1998
Crédit : IMCCE/Patrick Rocher
Cette figure montre bien que la saison n'est pas fonction de la distance entre le Soleil et la Terre. Actuellement, dans l'hémisphère nord, la saison la plus froide (l'hiver) correspond à l'époque où le Soleil est le plus près de la Terre et la saison la plus chaude (l'été) correspond à l'époque où le Soleil est le plus loin de la Terre.
L'évolution de la longueur des saisons
Si les positions du périhélie et de l'aphélie du barycentre Terre-Lune étaient constantes dans le temps, la durée des différentes saisons serait, elle aussi, constante. Mais l'orbite du barycentre Terre-Lune tourne dans son plan dans le sens direct à raison d'environ 12" par an (soit une révolution en environ 100 000 ans), ce mouvement est donc un mouvement direct de la ligne des apsides. La précession des équinoxes
s'effectue dans le sens contraire (sens rétrograde) à raison de 50,288200" par année julienne de 365,25 jours (soit une révolution en environ 26000 ans). La combinaison de ces deux mouvements permet de calculer la période du passage du périhélie de la Terre par la direction de l'équinoxe de printemps, cette période d'environ 21 000 ans est appelée précession climatique. En effet, tous les 10500 ans (demi-période de la précession climatique) l'aphélie passe de l'été à l'hiver. Or même si la distance Terre-Soleil n'est pas le facteur prédominant dans la nature des saisons, la combinaison du passage de la Terre à l'aphélie en hiver donne des hivers plus rudes. De même la distance Terre-Soleil dépend également de la variation de l'excentricité de l'orbite terrestre. Ainsi les périodes glacières sont corrélées avec les minima de l'excentricité de l'orbite terrestre.

Mouvement de l'équinoxe et de l'axe des apsides
Crédit : IMCCE/Patrick Rocher
Conclusion
 Conclusion
Conclusion
L'inégalité de la longueur des saisons est due à la non uniformité du mouvement orbital de la Terre autour du Soleil. La variation des longueurs des saisons est due au mouvement de la ligne des apsides de la Terre.
Historique : saisons
Introduction
 Introduction
Introduction
Cette section traite des aspects historiques et géographiques des saisons. Très tôt les astronomes ont essayé de construire des calendriers solaires, pour cela ils durent mesurer et estimer la durée de l'année tropique. En fonction des lieux géographiques, les autres facteurs climatiques jouent des rôles plus ou moins prononcés, ainsi le nombre des saisons climatiques n'est pas toujours égal aux quatre saisons astronomiques.
Historique: La précession des équinoxes et la longueur de l'année tropique
Le nom d'Hipparque de Nicée (env. 190 - env. 125 av. J.-C.) est lié à la découverte de la précession des équinoxes.
Pour découvrir ce lent mouvement de la ligne des équinoxes, deux méthodes d'observations sont possibles. La
première consiste à mesurer les variations des longitudes des étoiles au cours du temps. Cette méthode est cumulative, car chaque année la longitude croit d'une valeur faible mais constante. La deuxième méthode consiste à mesurer l'écart entre l'année tropique et l'année sidérale. Nous savons grâce à Ptolémée (IIe siècle après J.-C.) qu'Hipparque a utilisé ces deux méthodes. Et c'est vraisemblablement la première qui fut à l'origine de sa découverte de la précession des équinoxes. Pour cela il compara la distance de Spica dans l'Épi de la Vierge (l'étoile alpha Virginis) avec l'équinoxe d'automne aux dates des observations de Timocharis, observations faites entre 294 et 283 av. J.-C. et la valeur de cette même distance à son époque, et il trouva une variation dans la longitude de l'étoile de 2° sur la période de 160 ans séparant les deux mesures.
Pour la détermination des valeurs de l'année tropique et de l'année sidérale, Hipparque utilisa dans un premier temps des observations faites entre 162 et 128 av. J.-C., mais les valeurs calculées à partir de ces observations semblaient indiquer une valeur variable de l'année tropique en fonction du temps. Finalement, il se limita aux observations des solstices qu'il avait effectuées lui-même en 135 av. J.-C., aux observations faites par Aristarque en 280 av. J.-C. et aux observations faites par Méton, en 432 av. J.-C. Pour l'année tropique il trouva une valeur de 365 jours 1/4 moins 1/300 jour (soit 365 jours 5h 55m 12s) et pour l'année sidérale, il trouva une valeur de 365 jours 1/4 plus 1/144 jour (soit 365 jours 6h 10m 0s). Ces valeurs sont assez proches des valeurs actuelles.
En réalité la valeur de l'année tropique n'est pas constante, mais varie lentement en fonction du temps, sa valeur est donnée pour un instant donné par la relation suivante (P. Bretagnon, 2000) :
A =365,242 190 516 6 - 61,560 7 x 10 -6 T - 68,4 x 10 -9 T 2 + 263,0 x 10 -9 T 3+ 3,2 x 10 -9 T 4
où T = (JJD - 2 451 545,0) / 365 250
JJD étant le jour julien de l'époque considérée.
valeurs de l'année tropique
| Epoque |
Auteur |
Valeur |
| 141-127 av. J.-C. |
Hipparque |
365j 5h 55m 12s |
| 45 av. J.-C. |
Jules César (Sosigène) |
365j 5h 55m |
| 139 ap J.-C. |
Ptolémée |
365j 5h 55m 12s |
| 499 |
Aryabhata |
365j 8h 36m 30s |
| 882 |
al-Battani |
365j 5h 48m 24s |
| ~1100 |
Khayam |
365j 5h 49m 12s |
| 1252 |
Tables Alphonsines |
365j 5h 49m 16s |
| ~1440 |
Ulug Beg |
365j 5h 49m 15s |
| 1543 |
Copernic |
365j 5h 49m 29s |
| 1574-1575 |
Danti |
365j 5h 48m |
| 1582 |
Calendrier Grégorien |
365j 5h 48m 20s |
| 2000 |
Bretagnon |
365j 5h 48m 45.26s |
Le tableau suivant donne les différentes valeurs de l'année tropique en fonction de l'époque.
Historique: La longueur des saisons
Le Papyrus d'Eudoxe, nous informe que Callipe (vers 370-330 av. J.-C.) fut un des premiers astronomes à déterminer avec précision la longueur des différentes saisons. Il trouva (94, 92, 89 et 90 jours) à partir de l'équinoxe de printemps.
Hipparque améliora ces valeurs et trouva (94 1/2, 92 1/2, 88 1/8 et 90 1/8) toujours à partir de l'équinoxe de
printemps. On remarquera que ces valeurs sont très différentes des valeurs actuelles et cela est normal. En effet, si l'on tient compte de la précession climatique, l'angle entre le périhélie et l'équinoxe de printemps était à l'époque d'Hipparque 34° plus grand qu'actuellement. Le périhélie tombait donc en automne et l'aphélie au printemps, et la saison la plus courte était effectivement l'automne et la saison la plus longue, le printemps.
Historique: Le nombre des saisons et le climat
Les variations de la hauteur du Soleil dans la journée est un des éléments moteurs du climat, ainsi plus on monte en latitude vers les pôles plus le Soleil reste bas sur l'horizon et plus on s'approche de l'équateur plus le Soleil monte haut dans le ciel. D'autres éléments -- la présence des mers et des océans, la présence de la végétation, la nature du relief -- interviennent localement et produisent les différents types de climats observables sur Terre. Ainsi si sous nos latitudes les quatre saisons sont relativement en phase avec les variations climatiques, dans d'autres régions les quatre saisons sont moins marquées et historiquement, leurs nombres et leurs durées sont différentes.
Deux saisons : en Mésopotamie, au Soudan
En Mésopotamie, l'année solaire est divisée en deux saisons de six mois chacune : l'été ou temps de chaleur, (en
sumérien Emesh, en akkadien ummatum) commence à l'équinoxe de printemps, et l'hiver ou temps du froid (en
sumérien Enten, en akkadien kussu) commence à l'éqinoxe d'automne. C'est plutôt le régime des pluies débutant vers le mois de septembre et la crue du Tigre et de l'Euphrate croissante de novembre à mars et maximale en avril et mai, éléments déterminant pour les travaux agricoles, qui sont à l'origine de ce découpage en deux saisons.
On retrouve une pratique identique de nos jours, chez les Nuer du Haut Nil (au Soudan) où l'année est divisée en deux saisons. Une saison des pluies de mars à septembre durant laquelle les Nuer mènent une vie sédentaire et une saison de sècheresse d'octobre à février où les Nuer reprennent une vie nomade.
Historique: Trois saisons : en Égypte ancienne
Dans l'Égypte ancienne, le nombre de saisons était de trois, chaque saison comportait quatre mois. Les noms des
saisons et des mois sont donnés dans le tableau suivant :
Saisons Égypte
| Saison |
Nom des mois |
| Inondation (Aklet) |
Thot-Paophi-Athyr-Choeac |
| Hiver (Peret) |
Tybi-Méchir-Phaminoth-Pharmouti |
| Été (Shemou) |
Pachon-Payni-Epiphi-Mésori |
L'année commence avec la saison de l'inondation et cela correspond au début de la crue du Nil. On lit souvent que la crue du Nil correspondait avec le lever héliaque de l'étoile Sirius (Sothis chez les égyptiens), et que le lever héliaque de Sirius a lieu le jour du solstice d'été. En réalité la crue du Nil est bien évidement liée à un phénomène saisonnier et ce phénomène a du, à une époque donnée, correspondre au lever héliaque de Sirius, mais le lever héliaque de Sirius ne se produit pas à date fixe, sa date varie avec la précession des équinoxes et dépend également de la latitude du lieu d'observation.
Historique: Quatre saisons décalées : en Chine
En Chine, l'année tropique est divisée en 24 sections de saisons - les Jié Qì - correspondant chacune à un arc de 15 degrés de longitude, on distingue quatre saisons comme sous nos latitudes, mais elles sont décalées par rapport aux nôtres d'un mois et demi. Ainsi contrairement aux conventions occidentales, les saisons débutent lorsque la longitudes du Soleil atteint 315°, 45°, 135° et 225° (pour le printemps, l'été, l'automne et l'hiver) et non pas aux équinoxes et aux solstices. Le printemps commence donc à mi-chemin entre le solstice d'hiver et l'équinoxe de printemps.
Dans les Jiè Qì les termes principaux Z sont appelés zhong qì.
Liste des Jié Qì
| Numéro |
Jié Qi |
Nom |
Longitude du Soleil |
| J1 |
Lì chun |
début du printemps |
315° |
| Z1 |
Yu shui |
pluies |
330° |
| J2 |
Jing zhé |
réveil des insectes |
345° |
| Z2 |
Chun fen |
équinoxe de printemps |
360° |
| J3 |
Qinq ming |
clarté |
15° |
| Z3 |
Gu yu |
pluies des grains |
30° |
| J4 |
Lì xià |
début de l'été |
45° |
| Z4 |
Xiao man |
petite abondance |
60° |
| J5 |
Máng zhong |
grains en épi |
75° |
| Z5 |
Xià zhì |
solstice d'été |
90° |
| J6 |
Xiao shu |
petite chaleurs |
105° |
| Z6 |
Dà shu |
grandes chaleurs |
120° |
| J7 |
Lì qiu |
début de l'automne |
135° |
| Z7 |
Chu shu |
fin des chaleurs |
150° |
| J8 |
Bái lù |
rosée blanche |
165° |
| Z8 |
Qiu fen |
équinoxe d'automne |
180° |
| J9 |
Hán lù |
rosée froide |
195° |
| Z9 |
Shuang Jiáng |
arrivée du givre |
210° |
| J10 |
Lì dong |
début de l'hiver |
225° |
| Z10 |
Xiao xue |
petites neiges |
240° |
| J11 |
Dà xue |
grandes neiges |
255° |
| Z11 |
Dong zhì |
solstice d'hiver |
270° |
| J12 |
Xiao hán |
petits froids |
285° |
| Z12 |
Dà hán |
grands froids |
300° |
Le tableau donne la liste des Jié Qì.
Historique: Cinq saisons : en Australie
Les aborigènes de la région de Kakadu (Australie) découpent l'année solaire en cinq saisons. En Gundjeidmi, la langue des Maiili, les saisons portent les noms suivants :
Saisons Kakadu
| Nom des saisons |
Traduction |
| yegge |
saison plus fraîche, mais encore humide |
| wurrgeng |
saison froide |
| gurrung |
saison chaude et sèche |
| gunumeleng |
saison des tempêtes d'avant la mousson |
| banggereng |
saison des tempêtes renverse tout |
Historique: Six saisons : en Inde
En Inde le nombre des saisons est de six, chaque saison ayant deux mois.
Le tableau suivant donne la liste des saisons ainsi que les mois du calendrier solaire indien correspondant à ces saisons avant la réforme calendaire de 1957.
Saisons Inde
| Saison |
Nom des mois dans le calendrier solaire |
| Hiver (Sisira) |
Pausa - Magha |
| Printemps (Vasanta) |
Phalguna - Chaitra |
| Été (Grisma) |
Vaisakha - Jyaistha |
| Pluies (Varsa) |
Asadha - Sravana |
| Automne (Sarat) |
Bhadra - Asvina |
| Froid (Hermana) |
Kartika - Agrahayana |
Les mois en Inde
La réforme du calendrier de 1957 a imposé un calendrier solaire identique au calendrier grégorien commençant le 1 Chaitra (22 mars). Dans ce nouveau calendrier, suite à la précession des équinoxes, les dates des saisons ont été décalées d'un mois pour compenser cet écart (qui est en réalité de six semaines).
Historique: Plus de six saisons
Assez paradoxalement, c'est au nord du cercle polaire que l'on trouve une division de l'année comportant plus de six saisons. Les Inuit utilisaient un calendrier lunaire, qui était en réalité plus lié aux variations de leur l'environnement qu'à l'observation de la Lune. Ce calendrier était composé de 13 mois lunaires. Les saisons étaient au nombre de huit et étaient, elles aussi, très liées aux modifications apparentes de l'environnement. De nos jours, ce découpage calendaire n'a plus cours chez les Inuit, il a été remplacé par le calendrier grégorien.
Saisons Inuit
| Nom des mois lunaires |
Saisons |
| Siqinnaarut (Soleil possible) |
Ukiuq (hiver) |
| Quangattaasan (Soleil plus haut) |
Ukiuq (hiver) |
| Avunniit (bébés phoques prématurés) |
Upirngaksajaaq (vers le printemps) |
| Naittian (bébés phoques) |
Upirngaksaaq (début du printemps) |
| Tirigluit (bébés phoques à barbe) |
Upirngaaq (printemps) |
| Nurrait (bébés caribous) |
Upirngaaq (printemps) |
| Manniit (oeufs) |
Upirngaaq (printemps) |
| Saggaruut (les caribous perdent leurs poils) |
Aujaq (été) |
| Akullirut (le poil des caribous épaissit) |
Aujaq (été) |
| Amiraijaut (les bois des caribous perdent du duvet) |
Ukiatsajaaq (vers l'automne) |
| Ukuitlirut (début de l'hiver) |
Ukiaksaaq (automne) |
| Tusartuut (écoute nouvelles des voisins) |
Ukiaq (début de l'hiver) |
| Tauvigjuaq (grande obscurité) |
Ukiuq (hiver) |
Le tableau suivant donne la liste des treize mois lunaires et les saisons correspondantes.
Conclusion
 Conclusion
Conclusion
Dès l'époque d'Hipparque (environ 130 avant J.-C.) les astronomes eurent une assez bonne approximation de la valeur de l'année tropique. A la date de la création de notre calendrier en 1582, la valeur utilisée était pratiquement la même que celle déterminée par Al Battani sept siècles plus tôt. Les valeurs actuelles ne sont pas mesurées mais calculées à partir des théories planétaires et du mouvement de précession des équinoxes.
Dans de très nombreux pays le nombre des saisons est différent des quatre saisons astronomiques, cela en raison de l'importance des autres facteurs climatiques prépondérants dans ces régions.
Conclusion
 Conclusion
Conclusion
Les saisons astronomiques sont des phénomènes astronomiques simples produits par l'inclinaison l'axe de rotation de la Terre par rapport au plan de son orbite. Elles gouvernent en partie le climat sur Terre. Leurs longueurs sont différentes et évoluent avec le temps. Elles servent de repère dans la vie de tous les jours et sont à l'origine de notre calendrier.
Les mouvements de la Terre et de la Lune
Auteur: Patrick Rocher
Introduction
 Prérequis
Prérequis
Aucun
 Introduction
Introduction
Nous présentons d'abord les mouvements de la Terre autour du soleil en décrivant les éléments orbitaux képlérien. Nous traitons ensuite les mouvements de la Lune autour de la Terre en définissant les éléments elliptiques, puis en décrivant différentes périodes de révolutions. Finalement nous présentons les phases de la Lune.
Résumé
Les mouvements de la Terre et de la Lune seront abordés dans un premier temps, puis les phases de la Lune.
Présentation historique
Introduction
 Introduction
Introduction
Dans la quasi-totalité des cultures anciennes et des sociétés sans écriture, les éclipses de Lune et plus encore les éclipses de Soleil, ont été attribuées à des causes surnaturelles, l'intervention d'un dieu, d'un démon ou d'un animal maléfique essayant d'éteindre ou de dévorer l'un des deux luminaires.
Les représentations mythologiques
Ainsi en Asie, un dragon céleste essayait de dévorer la Lune et le Soleil, d'ailleurs le plus ancien mot chinois pour décrire une éclipse, shih, signifie manger. De même en Inde les deux parties décapitées du démon Vichnou, Rahu et Ketu placées aux noeuds de l'orbite lunaire cherchaient à dévorer la Lune et le Soleil. Chez les Mayas, l'éclipse de Soleil est représentée par un serpent mordant le Soleil, au Yucatán, on l'appelle Chibil Chin ce qui signifie textuellement «Morsure du Soleil», de nos jours certains Mayas, tels que les Yucatèques ou les Chols considèrent les éclipses comme une bataille entre le Soleil et la Lune, ils déconseillent aux femmes enceintes d'observer ce phénomène sous peine de mettre au monde un enfant difforme! Les Aztèques ont aussi élaboré des théories concernant les éclipses de Soleil : au cours des éclipses un monstre appelé Tzitzimine descend sur Terre pour dévorer l'humanité, seule une série de sacrifices peut conjurer ce danger. Dans la mythologie germanique, le Soleil et la Lune sont poursuivis par deux loups célestes, Moongarm et Fenris et c'est la lutte entre ces deux monstres qui provoque les éclipses. Comme on le constate toutes les représentations mythologiques des éclipses ont un aspect néfaste, on conjurait ce mauvais sort de différentes façons : en faisant du bruit, en tirant des flèches sur le monstre dévoreur, en entrant dans l'eau ou plus grave à l'aide de sacrifices.
Cette peur engendrée par les éclipses va inciter les astronomes et astrologues de l'Antiquité à prédire le retour de ces phénomènes célestes. Le concept du dragon dévoreur de Lune et de Soleil a été repris par les grecs et les romains, c'est pour cette raison que les noeuds de l'orbite lunaire portent les noms de Caput et Cauda Draconis (la tête et la queue du dragon) et que l'intervalle séparant deux passages de la Lune par un des noeuds de son orbite porte le nom de révolution draconitique.
Il faut noter que bien que ces phénomènes soient parfaitement expliqués, on trouve encore, à la fin du XXe siècle des olibrius pour prédire la fin du monde et la chute de la station MIR place de la Concorde le jour de l'éclipse de Soleil du 11 août 1999. Le plus grave n'étant pas la prédiction en elle-même mais sa diffusion massive par les médias !
Mouvement de la Terre
Introduction
 Introduction
Introduction
Dans cette section nous allons présenter les paramètres orbitaux de la Terre dans le plan défini par sa trajectoire.
Mouvement de la Terre autour du Soleil
En première approximation on peut supposer que le mouvement de la Terre autour du Soleil obéit aux trois lois de Kepler. La Terre parcourt donc une orbite elliptique plane autour du Soleil, le Soleil étant situé à l'un des foyers de l'ellipse. Le plan de cette orbite s'appelle le plan de l'écliptique, car c'est lorsque la pleine Lune ou la nouvelle Lune est proche de ce plan qu'il y a une possibilité d'éclipses de Lune ou de Soleil. Ce plan sert de plan de base (Oxy) au repère de coordonnées polaires écliptiques, l'axe Oz de ce repère est normal au plan de l'écliptique et il est orienté de sorte que la trajectoire de la Terre soit dans le sens direct. Les deux coordonnées angulaires polaires écliptiques portent les noms de longitude écliptique et de latitude écliptique. Dans ce modèle keplerien du mouvement de la Terre, la latitude de la Terre est toujours nulle. Sur son orbite la Terre passe par deux positions particulières situées aux extrémités de la ligne des apsides (le grand-axe de l'ellipse) : l'aphélie correspondant à la distance maximale entre la Terre et le Soleil, et le périhélie correspondant à la distance minimale entre la Terre et le Soleil. Suite à la deuxième loi de Kepler, à l'aphélie la vitesse de la Terre est minimale et au périhélie elle est maximale. Ainsi la vitesse angulaire de la Terre progresse 7% plus vite au périhélie qu'à l'aphélie.
Dans l'étude des éclipses, on utilise le mouvement apparent du Soleil autour de la Terre. Dans ce mouvement le Soleil parcourt une orbite elliptique autour de la Terre, l'orbite a les mêmes caractéristiques que la trajectoire de la Terre autour du Soleil. Cette représentation est correcte d'un point de vue cinématique (changement d'origine du repère), mais n'a aucun sens d'un point de vue dynamique.
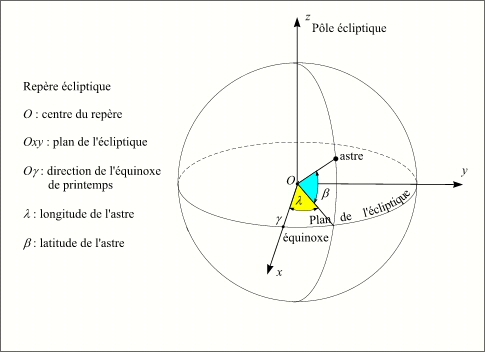
Sphère céleste écliptique.
Crédit : IMCCE/Patrick Rocher
En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre
 En savoir plus
En savoir plus
Le mouvement elliptique de la Terre a lieu dans le plan de l'écliptique, l'ellipse est donc définie géométriquement par la connaissance de la longitude du périastre : ω (angle formé par son demi-grand axe et l'axe Ox), de son demi-grand axe a et de son excentricité e. Le mouvement de la Terre sur l'ellipse est connu lorsque l'on connaît pour une date origine T0 sa longitude λ et son moyen mouvement n.
En réalité, suite aux perturbations planétaires l'orbite de la Terre n'est pas keplerienne et ses éléments orbitaux ne sont pas constants mais varient avec le temps.
Le tableau suivant donne les éléments moyens de l'orbite de la Terre dans le repère défini par l'équinoxe et l'écliptique moyens dynamiques inertiels de la date (J2000).
| Paramètres de l'orbite |
Valeurs au 1er janvier 2000 à 12h |
| demi-grand axe : a
|
1,000 001 017 8 ua |
| excentricité : e
|
0,016 708 634 2 |
| longitude du périhélie : ϖ
|
102,937 348 08° |
| longitude de la Terre : λ
|
100,466 456 83° |
| moyen mouvement : n
|
1296027711,03429"/millier d'année julienne ~ 0,985 647 358°/jour |
Comme ces éléments sont donnés dans le repère moyen de la date, repère tenant compte de la précession des équinoxes, l'inclinaison de l'orbite est nulle et le rapport 360°/n donne la période de révolution tropique de la Terre autour du Soleil (365,2421904 jours). Pour avoir la révolution sidérale de la Terre (365,2563632 jours), il faut utiliser le moyen mouvement donné dans le repère fixe J2000 (n = 0,9856091125°/jour).
En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre-2
 En savoir plus
En savoir plus
- La distance entre le Soleil et la Terre au périhélie est donnée par la formule Δ = a . (1 - e).
- La distance entre le Soleil et la Terre à l'aphélie est donnée par la formule Δ = a . (1 + e).
- Le demi-grand axe a, le demi-petit axe b et l'excentricité e sont liés par la relation suivante : e2 = (a2 - b2) / a2.
- La distance c entre le centre de l'ellipse et un de ses foyers est donnée par c = e.a
- Le diamètre apparent D du Soleil vu du centre de la Terre est donné par la formule : D = 2 arctg(Rs/Δ), où Δ est la distance Terre-Soleil et Rs le rayon du disque solaire.
- Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler : n2 a3 = constante.
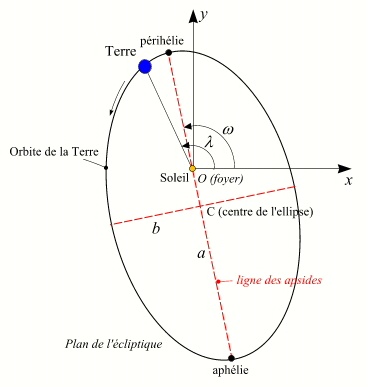
Éléments de l'orbite keplerienne de la Terre;
Crédit : IMCCE/Patrick Rocher
 Remarque
Remarque
Sur cette figure l'excentricité de l'orbite terrestre a été fortement exagérée.
Exercice
 Orbite de la Terre
Orbite de la Terre
 Remarque
Remarque
Le tracé de l'orbite de la Terre autour du Soleil en prenant a = 10 cm est un cercle. En effet la différence entre le demi-grand axe et de demi-petit axe est d'environ 14 μm, elle est donc dans l'épaisseur du trait. Par contre, sur la figure, le Soleil n'occupe pas le centre du cercle mais est excentré d'environ 1,7 mm
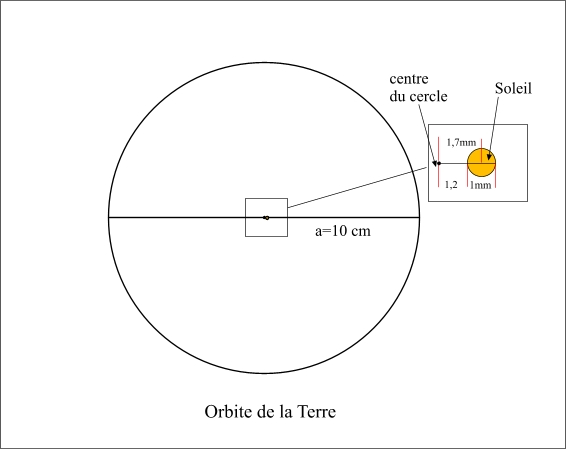
Orbite de la Terre.
Crédit : IMCCE/Patrick Rocher
Question 1)
En utilisant les éléments orbitaux de la Terre donnés dans le supplément de cours, calculer la valeur du demi-petit axe b de l'ellipse, la distance c entre le centre de l'ellipse et son foyer. Puis calculer les distances Terre-Soleil lorsque la Terre est au périhélie et lorsque la Terre est à l'aphélie. Exprimer ces résultats en unités astronomiques, puis en kilomètres en prenant : 1 ua = 149597870 km.
En déduire les valeurs du diamètre apparent du Soleil vu du centre de la Terre, lorsque la Terre est à l'aphélie et lorsque la Terre est au périhélie, on prendra le rayon solaire égal à 696000km. Ensuite, faire un dessin à l'échelle en prenant comme demi-grand axe de l'orbite terrestre une valeur de 10 cm. Calculer les valeurs précédentes à cette échelle, calculer la valeur de a - b.
Que peut-on en conclure ?
Mouvement orbital de la Lune
Introduction
 Introduction
Introduction
Cette section décrit le mouvement orbital de la Lune par rapport au Soleil. Le problème qui était plan dans le cas de la Terre devient spatial car le plan de l'orbite lunaire n'est pas confondu avec le plan de l'orbite terrestre. Il convient donc d'ajouter de paramètres supplémentaires pour positionner le plan de l'orbite par rapport au repère fondamental (plan de l'écliptique ou de l'équateur).
La mouvement de la Lune autour de la Terre
Contrairement au mouvement de la Terre autour du Soleil, qui peut être considéré en première approximation comme keplerien (solution exacte du problème des deux corps), le mouvement de la Lune est beaucoup plus complexe. Une première approximation du mouvement de la Lune est donnée par la résolution d'un problème des trois corps (Soleil, Terre et Lune) appelé problème principal. Dans ce problème le mouvement de la Lune est obtenu en tenant compte de l'attraction du centre de masse de la Terre et des perturbations solaires dans le cadre de la mécanique newtonienne, le mouvement du barycentre Terre-Lune étant représenté par un mouvement keplerien.
La solution complète tient compte de très nombreuses perturbations et les éléments elliptiques se présentent sous la forme de séries semi-analytiques comportant plusieurs milliers de termes, environ 35000 pour la solution ELP2000 de Michèle Chapront-Touzé et Jean Chapront.
Les éléments elliptiques de l'orbite lunaire ne sont donc pas constants, mais varient rapidement avec le temps. Les valeurs du demi-grand axe, de l'excentricité et de l'inclinaison oscillent autour de valeurs moyennes ; la ligne des noeuds de l'orbite et la ligne des apsides sont animées de mouvements circulaires non uniformes.
En tenant compte de ces perturbations, la vitesse angulaire de la Lune peut progresser 29% plus vite à son périgée qu'à son apogée. La variation de distance entre le centre de la Terre et le centre de la Lune va de 56 à 63,8 rayons terrestres selon que la Lune est à son périgée ou à son apogée (la distance moyenne est de 60 rayons terrestres).
En savoir plus: La définition des éléments elliptiques
 En savoir plus
En savoir plus
Les éléments elliptiques sont une série de six paramètres permettant de définir parfaitement une orbite elliptique keplerienne dans le repère écliptique céleste. L'orbite elliptique keplerienne étant la trajectoire d'un corps M gravitant autour d'un corps principal S pour une époque initiale donnée t0.
Trois paramètres déterminent les caractéristiques de l'ellipse et du mouvement du corps dans le plan de l'orbite :
- le demi-grand axe a de l'ellipse,
- l'excentricité e de l'ellipse,
- l'anomalie vraie υ du corps pour l'époque donnée, c'est l'angle formé par la direction du périastre et la direction du corps vues du foyer de l'ellipse.
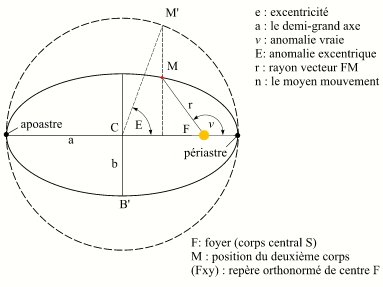
Paramètres de l'ellipse keplerienne.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre donne une représentation de ces paramètres ainsi que d'autres paramètres liés au mouvement elliptique.
En savoir plus: La définition des éléments elliptiques-2
 En savoir plus
En savoir plus
Les formules du problème des deux corps permettent de calculer la position de l'astre sur son orbite pour un instant t quelconque.
L'anomalie moyenne M (parfois notée l dans le cas de la Lune) est donnée par M = n.(t - t0) où n est le moyen mouvement.
Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler (n2 a3 = constante).
On passe de l'anomalie moyenne M à l'anomalie excentrique E en résolvant l'équation de Kepler : E - e sin E = M. Cette équation se résout par itérations successives.
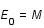
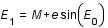
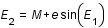
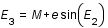 et ainsi de suite.
et ainsi de suite.
Enfin, connaissant l'anomalie excentrique E, l'anomalie vraie v et le rayon vecteur r sont donnés par les équations suivantes :
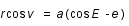
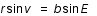
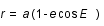
Le plan de l'orbite n'étant pas a priori dans le plan de l'écliptique, ces deux plans se coupent suivant une droite appelée ligne des noeuds ligne des noeuds. Cette ligne des noeuds coupe l'orbite du corps en deux points : le noeud ascendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes négatives aux latitudes positives et le noeud descendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes positives aux latitudes négatives.
En savoir plus: La définition des éléments elliptiques-3
 En savoir plus
En savoir plus
Trois angles permettent de positionner le plan de l'orbite dans l'espace :
- La longitude du noeud ascendant de l'orbite Ω, c'est l'angle formé par la direction de l'axe 0x et la direction du noeud ascendant de l'orbite,
- l'inclinaison de l'orbite i, c'est l'angle formé par le plan de l'écliptique et le plan de l'orbite,
- l'argument du périastre ω, c'est l'angle formé par la direction du noeud ascendant et la direction du périastre.
Parfois on donne l'angle ϖ = Ω + ω que l'on appelle longitude du périastre.
Éléments de l'orbite keplerienne
Crédit : IMCCE/Patrick Rocher
Mouvement de la Lune et périodes de révolution
Introduction
 Introduction
Introduction
Dans cette section nous allons définir les différentes périodes de révolution qui se rattachent au mouvement de la Lune. Les pages "pour en savoir plus" donnent les valeurs des différents paramètres orbitaux et leurs variations au cours du temps.
Périodes de révolutions de la Lune
Le tableau suivant donne les périodes de révolutions moyennes de la Lune.
| Nom de la période |
Durée en jours |
Définition |
| période sidérale |
27,321 661 547 |
retour dans la même direction par rapport aux étoiles |
| période anomalistique |
27,554 549 878 |
retour au périgée de l'orbite |
| période synodique |
29,530 588 853 |
retour de la même phase lunaire |
| période draconitique |
27,212 220 817 |
retour par le même noeud de l'orbite |
| période tropique |
27,321 582 249 |
retour par la direction de l'équinoxe. |
 Remarque
Remarque
Toutes les périodes décrites ci-dessus font intervenir la longitude moyenne de la Lune, ce sont donc des périodes de révolutions moyennes et non des périodes de révolutions vraies. Les périodes de révolutions vraies varient continuellement et ne sont pratiquement jamais égales aux périodes de révolutions moyennes. Ainsi, par exemple, l'intervalle de temps qui sépare deux nouvelles Lunes (lunaison vraie) peut présenter des écarts de plus ou moins 7h avec la valeur de la période synodique moyenne (lunaison moyenne).
En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire
 En savoir plus
En savoir plus
Le tableau suivant donne les éléments elliptiques moyens de la Lune rapportés à l'écliptique et à l'équinoxe moyens de la date pour l'époque J2000 (1 janvier 2000 à 12h).
| Éléments |
Valeurs |
Mouvements dus aux perturbations |
| Demi-grand axe a
|
383 397,7916 km |
|
| Excentricité e
|
0,055 545 526 |
|
| Inclinaison i
|
5,156 689 83° |
|
| Longitude du noeud Ω
|
125,044 555 04° |
mouvement rétrograde : (-19.3413618°/an) |
| Longitude du périgée ϖ
|
83,353 242 99° |
mouvement direct : (+40,690137°/an) |
| Longitude moyenne L
|
218,316 654 36° |
|
L'anomalie moyenne M de la Lune est donnée par : M = n (t - t0) où n est le moyen mouvement de la Lune.
En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire-2
 En savoir plus
En savoir plus
La longitude vraie de la Lune Λ est donnée par : Λ = Ω + ω + υ = ϖ + υ où υ est l'anomalie vraie.
La longitude moyenne de la Lune L est donnée par : L = Ω + ω + M = ϖ + M = ϖ + n (t - t0). La période de révolution de la longitude moyenne est égale à la révolution sidérale de la Lune, la période sidérale est l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune dans une même direction par rapport aux étoiles.
L'anomalie moyenne M = L - ω représente l'angle entre la direction du périgée et la longitude moyenne de la Lune, sa période de révolution s'appelle la période anomalistique, elle représente l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune à son périgée, elle diffère de la révolution sidérale car la ligne des apsides (donc le périgée) est animée d'un mouvement de rotation dans le sens direct.
L'angle D = L - Ls est la différence entre la longitude moyenne de la Lune et la longitude moyenne du Soleil. Les phases de la Lune sont liées, non à cet angle, mais à la différence entre les longitudes vraies des deux corps. Pour la nouvelle Lune, le premier quartier, la pleine Lune et le dernier quartier cette différence vaut respectivement 0°, 90°, 180° et 270°. Par contre la période moyenne qui ramène la Lune dans une même phase que l'on appelle la période synodique ou lunaison moyenne est la période de l'angle D.
L'angle F = L - Ω est la différence entre la longitude moyenne de la Lune et la direction du noeud ascendant de son orbite. Sa période de révolution s'appelle période draconitique, elle représente l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune au noeud ascendant de son orbite, elle diffère de la révolution sidérale car la ligne des noeuds est animée d'un mouvement de rotation dans le sens rétrograde.
En savoir plus: Les variations des éléments elliptiques de la Lune
 En savoir plus
En savoir plus
Nous avons vu que, sous l'action de nombreuses perturbations, les éléments orbitaux de la Lune ne sont pas constants, mais varient avec le temps. Le tableau suivant donne les plus grosses variations de ces éléments.
| Éléments |
Amplitude |
Période |
Amplitude |
Période |
|
a
|
3400,4 km |
14.76 j |
-635,6 km |
31,81j |
|
e
|
0,014217 |
31,81j |
0,008551 |
173,31j |
|
i
|
|
|
8,105' |
173,31j |
|
ϖ
|
-15,448° |
31,81j |
-9,642° |
205,9j |
|
Ω
|
|
|
-1,4979° |
173,31j |
On constate que ces variations présentent de très fortes amplitudes sur des périodes de temps relativement courtes. Ainsi l'excentricité varie de plus ou moins 0,014217 sur une période de 31,81 jours ce qui représente un écart de plus de 25% de la valeur moyenne !
En savoir plus: Les variations des éléments elliptiques de la Lune-2
 En savoir plus
En savoir plus
La série suivante donne les premiers termes permettant le calcul de la longitude vraie de la Lune ainsi que leur nom et l'époque de leur découverte :
Λ = L + (6,288 8° sin M + 0,213 6° sin 2M)
équation du centre : connue depuis Hipparque (~150 av. J.-C.)
+ 1,274 0° sin (2D - M)
évection (période 31,81 jours) : découverte par Ptolémée (milieu du IIe siècle)
+ 0,658 3° sin 2D
variation (période 14,76 jours) : découverte par Tycho Brahé (XVIe siècle)
- 0,185 1° sin M'
équation annuelle (période 1 an) : découverte par Tycho Brahé (XVIe siècle)
- 0,114 3° sin 2F
réduction à l'écliptique (période 13,6 jours)
 Remarque
Remarque
Comme on le verra par la suite, les diamètres apparents de la Lune et du Soleil vus depuis la Terre sont de l'ordre du demi-degré, donc pour prédire une éclipse du Soleil il faut obligatoirement connaître la position de ces deux corps avec une précision inférieure à ce demi-degré. Pour la Lune, il faut donc connaître l'équation du centre et l'évection, la connaissance de la variation n'est pas nécessaire car le terme sin 2D est nul à la pleine Lune et à la nouvelle Lune (D = 0° et D = 180°). Il était donc impossible de prédire la visibilité d'une éclipse de Soleil en un lieu donné avant le milieu du IIe siècle, époque de la découverte de l'évection par Claude Ptolémée.
Les phases de la Lune
Introduction
 Introduction
Introduction
Dans cette section nous allons étudier et décrire les phases lunaires et les différents noms qui leurs sont attribués.
Les phases de la Lune-1
Comme nous venons de le voir, la Lune tourne autour de la Terre dans un mouvement d'ouest en est (dans le sens direct). Elle effectue un tour complet autour de la Terre au cours d'une révolution sidérale de 27,321661547 jours. Au cours de sa révolution, depuis la Terre, on ne voit pas la partie éclairée de la Lune sous un même angle, cela constitue les phases de la Lune. On distingue quatre positions particulières.
Lorsque la Lune et le Soleil ont la même longitude, on dit qu'ils sont en conjonction, c'est la nouvelle Lune. Lorsque la longitude de la Lune est à 180° de la longitude du Soleil, on dit qu'ils sont en opposition, c'est la pleine Lune. À la nouvelle Lune, la Lune est devant le Soleil, elle se lève et se couche donc presque en même temps que lui. À la pleine Lune, la Lune est à l'opposée du Soleil, donc elle se lève lorsqu'il se couche et elle se couche lorsqu'il se lève. Ainsi la nouvelle Lune n'est levée que le jour et la pleine Lune n'est levée que la nuit. La pleine Lune et la nouvelle Lune portent également le nom de syzygies.
Les phases de la Lune-2
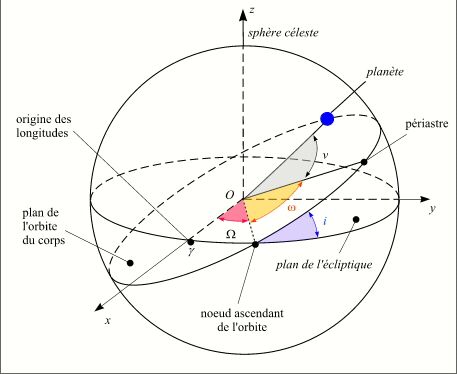
Les phases comprises entre la nouvelle Lune et la pleine Lune s'appellent phases croissantes et les phases comprises entre la pleine Lune et la nouvelle Lune s'appellent phases décroissantes. Lorsque la longitude de la Lune est à 90° vers l'est de la longitude du Soleil, on aperçoit uniquement une moitié du disque lunaire éclairé, c'est le premier quartier de Lune, on dit également que la Lune est en quadrature Est. Lorsque la longitude de la Lune est à 90° vers l'ouest (270° vers l'est) de la longitude du Soleil, on aperçoit l'autre moitié du disque lunaire éclairé, c'est le dernier quartier de Lune, on dit également que la Lune est en quadrature Ouest. Le premier quartier est donc compris entre la nouvelle Lune et la pleine Lune et le dernier quartier est compris entre la pleine Lune et la nouvelle Lune. Les aspects du premier et du dernier quartier de Lune sont inversés selon que l'on se trouve dans l'hémisphère nord ou dans l'hémisphère sud. Ainsi le premier quartier vu depuis l'hémisphère nord ressemble au dernier quartier vu depuis l'hémisphère sud et inversement. Le premier quartier se trouvant 90° à l'est du Soleil, il est visible l'après midi à l'est et dans la première partie de la nuit à l'ouest. Le dernier quartier étant à 90° à l'ouest du Soleil, il est visible la seconde moitié de la nuit à l'est et dans la matinée à l'ouest. Entre la nouvelle Lune et les quartiers de Lune, la phase lunaire a l'aspect d'un croissant, entre les quartiers et la pleine Lune, la Lune a la forme d'une bosse et on la qualifie de gibbeuse.
Les phases lunaires
Crédit : IMCCE/Patrick Rocher
Les phases de la Lune-3
Il y a éclipse de Soleil lorsque la Lune passe devant le Soleil et éclipse de Lune lorsque la Lune passe dans l'ombre de la Terre. Les éclipses de Soleil ont donc toujours lieu au voisinage de la conjonction (nouvelle Lune) et les éclipses de Lune ont toujours lieu au voisinage de l'opposition (pleine Lune). Si l'orbite de la Lune était dans le plan de l'orbite du Soleil apparent autour de la Terre (écliptique) il y aurait des éclipses de Soleil à chaque nouvelle Lune et des éclipses de Lune à chaque pleine Lune. Comme les éclipses de Soleil ont lieu à la nouvelle Lune, elles ne sont visibles en un lieu donné que le jour, cela parait évident. De même comme les éclipses de Lune ont lieu à la pleine Lune, elles ne sont visibles en un lieu donné que la nuit.
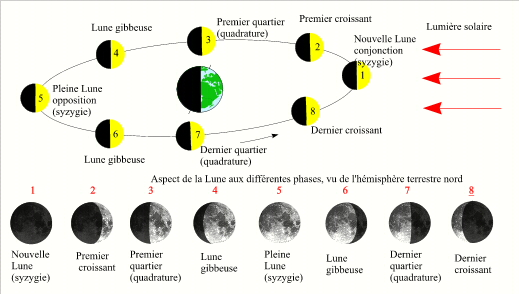
En savoir plus: La lunaison moyenne, le mois lunaire
 En savoir plus
En savoir plus
La lunaison moyenne est l'intervalle de temps qui s'écoule en moyenne entre deux mêmes phases, c'est la combinaison de deux mouvements moyens : le mouvement moyen de la Lune autour de la Terre, dont la période moyenne de révolution est la révolution sidérale de la Lune SL = 27,321661547 jours (27 jours 7h 43m 11,56s), et le mouvement moyen du Soleil apparent autour de la Terre (ou de la Terre autour du Soleil), dont la période moyenne de révolution est la révolution sidérale du Soleil (ou de la Terre) SS = 365,2563632 jours. Nous avons donc deux mouvements moyens de période SS et SL dans le même sens, l'intervalle de temps L qui sépare deux nouvelles Lunes, appelée révolution synodique moyenne, est solution de l'équation suivante :
1/SL - 1/SS = 1/L
En l'on trouve L = 29,53058885 jours soit 29 jours 12h 44m 2,88s.
La révolution synodique moyenne porte également les noms de lunaison moyenne et de mois lunaire moyen.
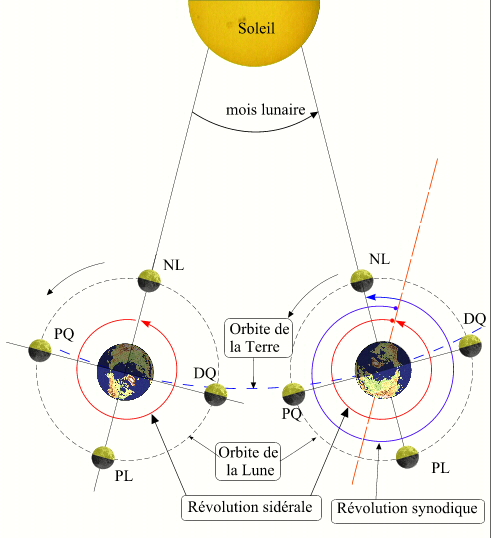
Révolutions sidérale et synodique
Crédit : IMCCE/Patrick Rocher
En savoir plus: La lunaison vraie
 En savoir plus
En savoir plus
La révolution synodique moyenne de la Lune correspond à une valeur moyenne, en réalité comme nous l'avons déjà vu ni le mouvement orbital de la Lune ni le mouvement orbital de la Terre ne sont uniformes. La vitesse angulaire de la Lune est maximale au périgée et minimale à l'apogée. De même la vitesse de la Terre est maximale en janvier lorsqu'elle est au périhélie et minimale en juillet lorsqu'elle est à l'aphélie. La lunaison vraie va donc être différente de la lunaison moyenne. De plus la période séparant deux nouvelles Lunes vraies ne sera pas égale à la période séparant deux pleines Lunes vraies. Le graphique ci-contre nous donne les écarts en heures et fraction d'heure entre la lunaison vraie et la lunaison moyenne. On constate que ces écarts peuvent atteindre plus ou moins sept heures, ce qui est énorme compte tenu de la vitesse angulaire de la Lune, l'écart en longitude entre la Lune vraie et la Lune moyenne peut atteindre jusqu'à 7,5°. Cette valeur est à comparer avec les diamètres apparents de la Lune et du Soleil (0,5°).
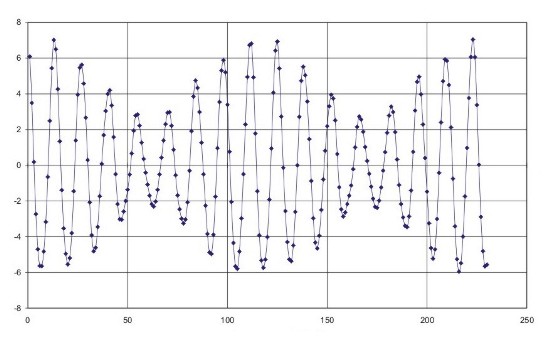
Écarts entre la lunaison vraie et la lunaison moyenne sur une période de 18,6 ans
Crédit : IMCCE/Patrick Rocher
Ce graphique fait également apparaître une période de 8,84 ans correspondant à la projection en longitude du mouvement du périgée de la Lune. En effet la ligne des apsides de la Lune tourne dans le sens direct dans le plan de l'orbite lunaire, ce mouvement projeté dans le plan de l'écliptique et combiné avec le mouvement rétrograde des noeuds de l'orbite lunaire produit un mouvement en longitude de la projection du périgée de 40,690137°/an soit une période d'environ 8,84 ans. Il est normal que l'on retrouve cette période dans la variation de la lunaison vraie car la vitesse angulaire de la Lune varie avec l'anomalie vraie.
Exercice
 Cacul de la lunaison moyenne
Cacul de la lunaison moyenne
Question 1)
Nous avons vu que la lunaison moyenne est la combinaison de deux mouvements : le mouvement moyen de la Lune autour de la Terre et le mouvement moyen du Soleil apparent autour de la Terre. Ces deux mouvements se font dans le même sens. Le calcul de la lunaison moyenne a été fait dans le cours à partir de la période de révolution sidérale de la Lune et de la révolution sidérale du Soleil. Refaites ce calcule à l'aide des révolutions tropiques de la Lune et du Soleil. Trouve-t-on la même valeur? Pourquoi?
On donne les valeurs suivantes :
révolution tropique de la Lune : TL = 27,321 582 249 jours,
révolution tropique de la Terre ( donc du Soleil apparent) : TS = 365,242 190 04 jours.
Les éclipses de Soleil
Auteur: Patrick Rocher
Introduction
 Prérequis
Prérequis
Il est vivement conseillé de lire le cours sur les mouvements de la Terre et de la Lune.
 Introduction
Introduction
Nous présentons d'abord les aspects géométriques des éclipses, c'est-à-dire les positions relatives des corps et leur taille apparente. Ces différents aspects géométriques permettent de définir les types d'éclipses. Puis nous décrivons les différentes phases générales et locales des éclipses, ainsi que des méthodes de calcul permettant de les obtenir. Nous terminerons cette section avec les différentes représentations cartographiques des zones de visibilité des éclipses solaires.
Résumé
Les différents types d'éclipses, leur géométrie et enfin les circonstances générales et locales des éclipses solaires ainsi que leurs paramètres caractéristiques.
Les différents types d'éclipses
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire les différents cas de figure qui peuvent se produire au moment de la conjonction entre la Lune et le Soleil. Nous en déduirons les différentes types d'éclipses de Soleil possibles selon que la Terre coupe ou ne coupe l'axe des cônes d'ombre ou de pénombre.
Dimensions et distances des corps
Le dessin ci-contre donne les rayons équatoriaux de la Terre, de la Lune et du Soleil, il donne également les distances moyennes entre ces corps, en kilomètres et en rayons terrestres. Comme on le constate, si l'on voulait réaliser un dessin comportant les trois corps il serait impossible de le faire à l'échelle. Ainsi si la Terre est représentée par un cercle de 2 cm de rayon, la Lune doit être représentée par un cercle de 0,55 cm situé à une distance d'environ 1,20 m de la Terre et si l'on voulait représenter le Soleil celui-ci aurait un rayon de 2,18 m et serait situé à 469 m de la Terre !
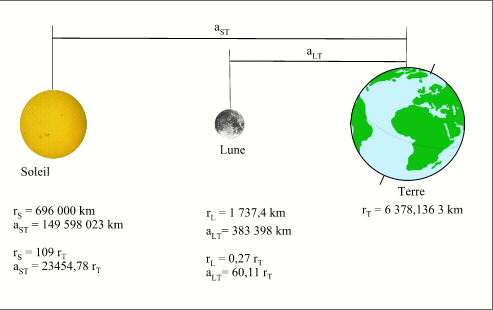
Crédit : IMCCE/Patrick Rocher
Aucun dessin représentant les trois corps n'est donc à l'échelle, et en ne respectant pas les distances et les tailles des corps, on introduit des distorsions dans les figures. Par exemple certaines droites quasi-parallèles se coupent suivant des angles qui sont beaucoup plus grands que la réalité.
Le cône d'ombre et le cône de pénombre
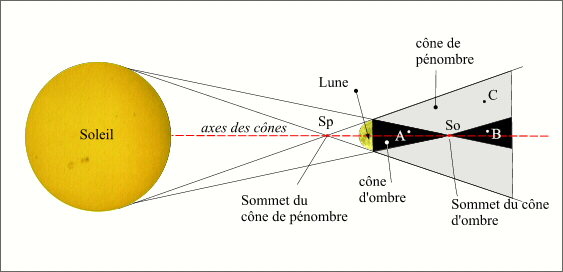
Cônes d'ombre et de pénombre
Crédit : IMCCE/Patrick Rocher
La Lune, éclairée par le Soleil, donne naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de la Lune constitue l'axe de ces cônes. Le sommet Sp du cône de pénombre est situé sur cet axe entre le Soleil et la Lune, et le sommet So du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport à la Lune. Le cône d'ombre est construit à l'aide des tangentes extérieures aux sphères solaire et lunaire, le cône de pénombre est construit à partir des tangentes intérieures aux sphères solaire et lunaire. Pour un observateur A placé dans le cône d'ombre, avant son sommet il y a éclipse totale du Soleil, pour un observateur B situé dans le prolongement du cône d'ombre, donc après le sommet du cône d'ombre, il y a éclipse annulaire du Soleil. Lorsqu'un observateur C se trouve dans le cône de pénombre, il assiste à une éclipse partielle, donc un passage partiel de la Lune devant le Soleil. En raison des variations de distances entre la Terre et la Lune, la Terre peut passer dans le cône d'ombre ou dans le prolongement du cône d'ombre.
Les différents types d'éclipses du soleil
Pas d'éclipse de Soleil
Souvent, au voisinage de la conjonction en longitude de la Lune et du Soleil (nouvelle Lune), au moment où la distance angulaire entre le centre de la Lune et le centre du Soleil vue depuis la Terre est minimale, la latitude de la Lune est trop grande et les cônes d'ombre et de pénombre ne rencontrent pas la surface terrestre. Alors, si la latitude de la Lune est positive, les cônes d'ombre et de pénombre passent au-dessus (au nord) de la Terre et si la latitude de la Lune est négative, les cônes d'ombre et de pénombre passent au-dessous (au sud) de la Terre. Dans ce cas il n'y a pas d'éclipse de Soleil.
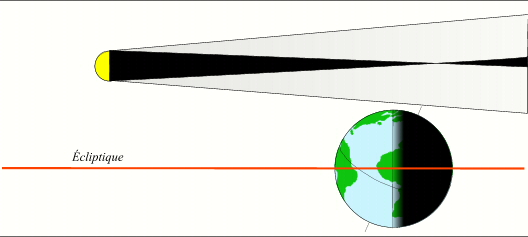
Pas d'éclipse de Soleil.
Crédit : IMCCE/Patrick Rocher
Les éclipses non centrales
Toujours au voisinage de la conjonction, lorsque l'axe des cônes d'ombre et de pénombre ne rencontrent pas la surface terrestre mais que le cône de pénombre et parfois également une partie du cône d'ombre rencontrent la Terre, il y a éclipse et l'on dit que l'éclipse est non centrale. On verra par la suite qu'une éclipse non centrale peut être totale, annulaire ou partielle.
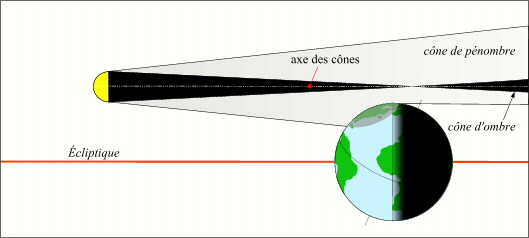
Éclipse non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses centrales
Toujours au voisinage de la conjonction, lorsque l'axe des cônes d'ombre et de pénombre rencontre la surface terrestre, il y a éclipse et l'on dit que l'éclipse est centrale. On verra par la suite qu'une éclipse centrale peut être totale, annulaire ou mixte (annulaire-totale).
L'ensemble de la surface terrestre parcourue durant une éclipse par le cône d'ombre où par son prolongement porte le nom de bande de centralité. L'intersection de l'axe des cônes d'ombre et de pénombre avec la surface terrestre, lorsqu'elle existe (éclipses centrales) porte le nom de ligne de centralité.
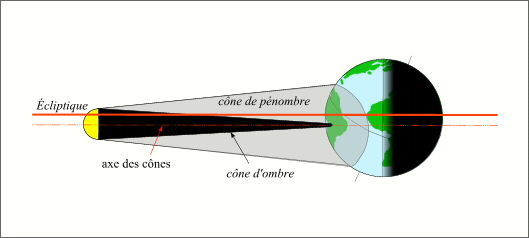
Éclipse centrale.
Crédit : IMCCE/Patrick Rocher
On remarquera que ces définitions portent uniquement sur la rencontre de l'axe des cônes d'ombre et de pénombre avec la surface terrestre.
Les éclipses totales
Lorsque la surface terrestre rencontre le cône d'ombre entre la Lune et le sommet du cône d'ombre, pour un observateur situé dans ce cône d'ombre la surface du Soleil est complètement occultée par la Lune, alors l'éclipse est dite totale. Le diamètre apparent de la Lune est supérieur au diamètre apparent du Soleil. La bande de centralité porte le nom de bande de totalité. Tous les observateurs situés sur cette bande de totalité observeront d'abord une phase partielle, puis la phase totale, puis de nouveau une phase partielle. Durant la phase de totalité la couronne solaire est observable. En début et en fin de phase de totalité un point brillant, appelé point de Baily, apparaît sur le limbe lunaire, ces points brillants proviennent de la lumière solaire passant par les vallées situées sur le limbe lunaire, ils annoncent le début et la fin de la phase de totalité.
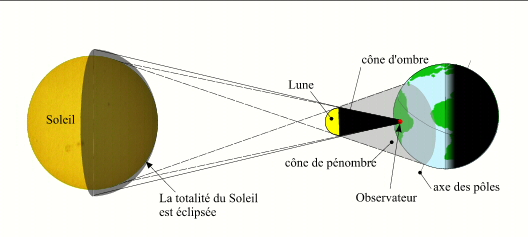
Éclipse totale centrale.
Crédit : IMCCE/Patrick Rocher

Photo de Christian Viladrich : éclipse totale du 26 février 1998.
Crédit : ASM
Les éclipses totales-2
Pour un observateur situé uniquement dans le cône de pénombre, une partie seulement du Soleil est occultée par la Lune, dans ce cas l'éclipse est vue par l'observateur sous la forme d'une éclipse partielle. Le diamètre apparent du Soleil est encore inférieur au diamètre apparent de la Lune.
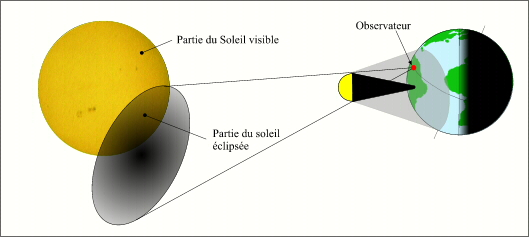
Phases partielles d'une éclipse totale.
Crédit : IMCCE/Patrick Rocher
Les éclipses totales non centrales
Il est possible que seule une petite partie du cône d'ombre rencontre la Terre sans que l'axe du cône d'ombre ne la rencontre. Dans ce cas, nous avons à faire à une éclipse totale non centrale, la bande de totalité est alors rasante à la surface de la Terre et la ligne de centralité n'existe pas. Sur la figure ci-contre, afin de la rendre plus lisible, nous avons ajouté une transparence au cône d'ombre pour voir que son axe ne rencontre pas la Terre, nous avons agrandi l'angle au sommet du cône d'ombre et nous avons supprimé le cône de pénombre.
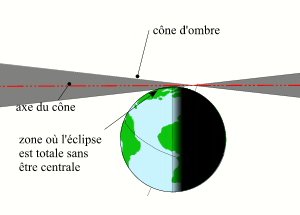
Éclipse totale non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires
Lorsque la surface terrestre rencontre le prolongement du cône d'ombre, pour un observateur situé dans ce prolongement du cône d'ombre la surface du Soleil n'est pas complètement occultée par la Lune et le diamètre apparent de la Lune est plus petit que le diamètre apparent du Soleil. Dans ce cas l'éclipse est dite éclipse annulaire. Tous les observateurs situés sur la bande de centralité observeront d'abord une phase partielle, puis la phase annulaire, puis de nouveau une phase partielle. Lors des éclipses annulaires la couronne solaire n'est pas visible.
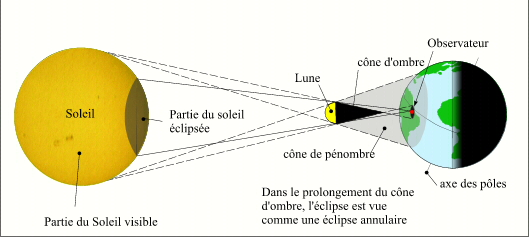
Éclipse annulaire centrale.
Crédit : IMCCE/Patrick Rocher

Phase annulaire.
Crédit : Christian Nitschelm
Les éclipses annulaires-2
Pour un observateur situé uniquement dans le cône de pénombre, une partie seulement du Soleil est occultée par la Lune. Dans ce cas l'éclipse sera vue par l'observateur sous la forme d'une éclipse partielle. Le diamètre apparent du Soleil est supérieur au diamètre apparent de la Lune.
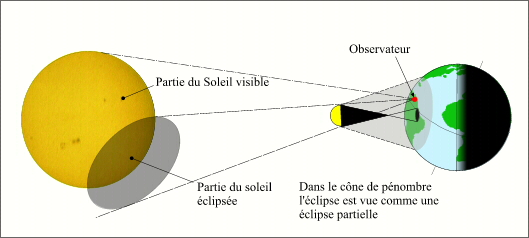
Phases partielles d'une éclipse annulaire.
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires non centrales
Comme pour les éclipses totales, il est possible que seule une petite partie du prolongement du cône d'ombre rencontre la Terre sans que l'axe du cône d'ombre ne la rencontre. Dans ce cas nous avons à faire à une éclipse annulaire non centrale, la bande de centralité est alors rasante à la surface de la Terre et la ligne de centralité n'existe pas. Sur la figure ci-contre, afin de la rendre plus lisible, nous avons ajouté une transparence au cône d'ombre pour voir que son axe ne rencontre pas la Terre, nous avons agrandi l'angle au sommet du cône d'ombre et nous avons supprimé le cône de pénombre.
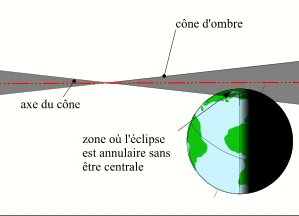
Éclipse annulaire non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses mixtes et les éclipses partielles
Soit d la distance entre la projection normale P du centre de la Terre sur l'axe du cône d'ombre et le sommet So du cône d'ombre. Si d est inférieure au rayon terrestre r et si P est situé après le sommet du cône d'ombre, alors le premier contact entre la Terre et le cône d'ombre se fait dans le prolongement du cône d'ombre et l'éclipse débute par une éclipse annulaire, puis l'intersection de la Terre et du cône d'ombre se fait au sommet du cône d'ombre puis en avant du sommet du cône d'ombre, l'éclipse est alors totale, puis de nouveau l'intersection entre la Terre et le cône d'ombre se fait au sommet du cône, puis dans le prolongement du cône d'ombre. Donc au cours de son trajet sur la surface terrestre, l'éclipse est d'abord annulaire, puis totale, puis de nouveau annulaire. Ce type d'éclipse s'appelle éclipse mixte ou éclipse annulaire-totale.
Elle est également appelée éclipse perlée, en effet, durant ces éclipses le diamètre apparent de la Lune est toujours très proche du diamètre apparent du Soleil car l'intersection reste toujours au voisinage du sommet du cône d'ombre; or le limbe lunaire n'est pas un cercle parfait car il est constitué par une succession de montagnes et de vallées, chaque vallée laisse passer la lumière solaire et parsème le limbe lunaire de nombreux points de Baily donnant au limbe l'aspect d'un collier de perles. De plus comme l'intersection du cône d'ombre et de la Terre se fait toujours au voisinage du sommet du cône d'ombre, les éclipses perlées sont caractérisées par une bande de centralité très étroite.
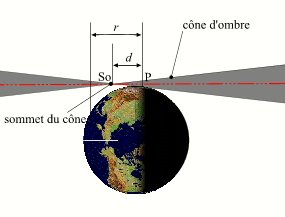
Géométrie des éclipses mixtes.
Crédit : IMCCE/Patrick Rocher
Les éclipses partielles
Enfin, lorsque la Terre rencontre uniquement le cône de pénombre de la Lune, seule une partie du Soleil est occultée et l'éclipse est dite partielle.
Exercice
La géométrie des éclipses de Soleil
Introduction
 Introduction
Introduction
Dans cette section, nous allons préciser la taille et la vitesse des l'intersections des cônes d'ombre et de pénombre avec la surface de la Terre. Puis nous définirons des paramètres caractéristiques des éclipses de Soleil : la magnitude et le degré obscuration.
Caractéristiques des cônes d'ombre et de pénombre
Les tailles
Le dessin ci-contre est trompeur, en effet nous avons représenté les trois corps sur la même figure et cela introduit, comme nous l'avons déjà signalé, des erreurs dans la taille des angles. Ainsi l'angle au sommet du cône de pénombre est de l'ordre du demi-degré. De même, le Soleil étant très loin, les tangentes T1 (extérieure) et T2 (intérieure) sont quasi-parallèles, donc le rayon d'une section normale au cône de pénombre au niveau de la Terre est très proche du diamètre de la Lune, donc le diamètre de la section normale du cône de pénombre au niveau de la Terre est de l'ordre de deux diamètres lunaires, soit environ 7000 km. Ainsi la pénombre ne recouvre jamais entièrement la surface terrestre, mais uniquement 16% d'un demi-hémisphère terrestre.
La taille du diamètre de la section normale au cône d'ombre au niveau de la Terre dépend des distances Terre-Lune et Soleil-Lune, on montre, à l'aide des valeurs extrêmes de ces distances que le diamètre de la section normale au cône d'ombre pour une éclipse totale est au maximum de 268 km et que le diamètre de la section normale au prolongement du cône d'ombre pour une éclipse annulaire est au maximum de 375 km. Bien évidemment l'ombre et le prolongement de l'ombre coupent la surface de la Terre suivant un ovale (intersection d'un cône et d'une sphère) dont le grand axe peut dépasser largement ces valeurs extrêmes, c'est le cas notamment pour les éclipses rasantes (proches des pôles).
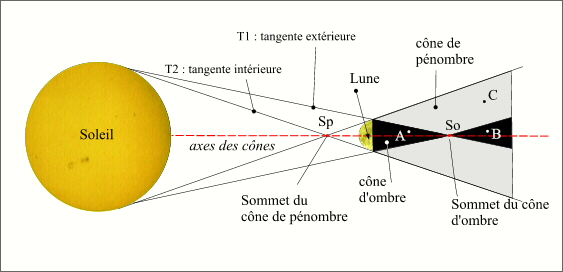
Différents types d'éclipses en fonction de la position de l'observateur.
Crédit : IMCCE/Patrick Rocher
Caractéristiques des cônes d'ombre et de pénombre-2
Les vitesses
La vitesse à laquelle se déplace l'ombre où le prolongement de l'ombre sur la surface de la Terre est la combinaison de deux mouvements : le mouvement de l'ombre dans l'espace qui est égal au mouvement de la Lune par rapport au Soleil vu depuis la Terre fixe et le mouvement de la surface terrestre du à la rotation de la Terre sur elle-même. Depuis la Terre, le Soleil et la Lune se déplacent par rapport aux étoiles d'ouest en est (mouvement direct), la Lune se déplace environ treize fois plus vite que le Soleil, son ombre se déplace d'environ 1 km/s par rapport à la Terre supposée fixe. La Terre tourne sur elle-même également d'ouest en est. La vitesse de l'ombre par rapport au sol est donc égale à la différence de la vitesse de l'ombre de la Lune et de la vitesse du sol. À l'équateur la vitesse du sol est de l'ordre de 500 m/s, la différence des deux vitesses est de 500m/s, plus on s'écarte en latitude de l'équateur, plus la vitesse de l'ombre est grande pour atteindre 1 km/s aux pôles (vitesse du sol nulle).
En savoir plus: Le calcul exact des vitesses : la vitesse de l'ombre à la surface terrestre
 En savoir plus
En savoir plus
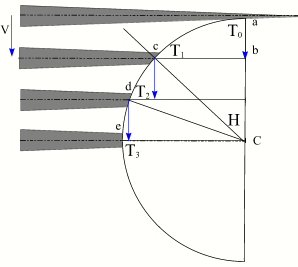
Vitesse de l'ombre à la surface d'une Terre fixe.
Crédit : IMCCE/Patrick Rocher
En réalité, le calcul de la vitesse de l'ombre à surface du sol est plus complexe, dans l'explication précédente nous avons fait des simplifications qui ne sont vraies que lorsque les vecteurs vitesses de l'ombre et du sol sont colinéaires. Dans un premier temps, on peut supposer une Terre fixe avec une ombre de la Lune se déplaçant avec une vitesse constante V par rapport à la Terre. Sur la figure ci-contre nous avons tracé la position du cône d'ombre et de son axe à des instants T0, T1, T2 et T3 séparés par un intervalle de temps dt constant. Durant le premier intervalle 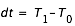 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 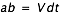 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
En savoir plus: Le calcul exact des vitesses : combinaison des vitesses
 En savoir plus
En savoir plus
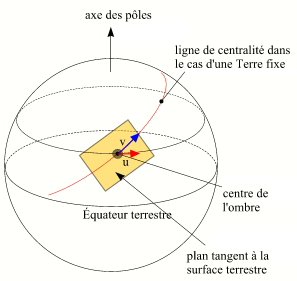
Combinaison des vitesses de l'ombre de la Lune et de la surface terrestre.
Crédit : IMCCE/Patrick Rocher
Pour avoir la vitesse, et la trajectoire, de l'ombre par rapport au sol dans le cas d'une Terre en rotation sur elle-même, il convient de combiner les deux mouvements. Si v est le vecteur vitesse de l'ombre (par rapport à la Terre fixe) dans le plan tangent au point de contact de l'axe du cône avec la surface terrestre et u le vecteur vitesse du sol dans le même plan, alors la vitesse de l'ombre par rapport au sol est égale à la différence des deux vecteurs vitesses (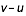 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
En savoir plus: Le calcul des rayons de l'ombre et de la pénombre
 En savoir plus
En savoir plus
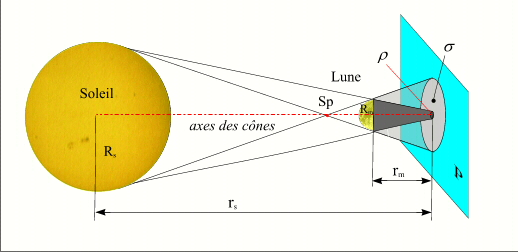
Éclipse totale : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Soit P un plan normal à l'axe des cônes d'ombre et de pénombre, ρ et σ les rayons des cercles définis par les intersections du cône de d'ombre et du cône de pénombre avec ce plan. Soit Rs le rayon solaire, Rm le rayon lunaire, rs et rm les distances respectives du centre du Soleil et du centre de la Lune au plan P. Une simple application du théorème de Thalès nous donne les valeurs de ρ et σ en fonction de Rs, Rm, rs et rm.
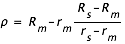
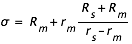
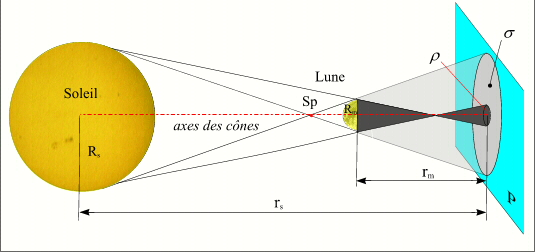
Éclipse annulaire : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Lorsque l'éclipse est annulaire le plan P coupe l'axe des cônes après le sommet du cône d'ombre, il coupe donc le prolongement du cône d'ombre. Les formules précédentes sont également applicables si l'on accepte que les rayons aient des valeurs négatives.
En savoir plus: Le calcul des rayons de l'ombre et de la pénombre-2
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes de ρ et σ en fonction des distances Terre-Soleil et Terre-Lune. Dans le tableau on se place d'abord dans le plan du centre de la Terre, puis l'on se place à la surface de la Terre avec les deux corps au zénith, les distance Terre-Lune et Terre-Soleil sont alors diminuées d'un rayon terrestre, en fait, on néglige le rayon terrestre devant la distance Terre-Soleil. Dans ce tableau le rayon solaire est pris égal à Rs = 696 000 km, le rayon lunaire est pris égal à Rm = 1738,1 km et le rayon terrestre est pris égal à Re = 6400 km. Nous donnons également ρ et σ en secondes d'arcs, dans ce cas, ces valeurs représentent les rayons sélénocentriques (vu depuis le centre de la Lune) apparents des intersections des cônes d'ombre et de pénombre avec le plan P.
|
Périgée |
Moyenne |
Apogée |
| rm
|
357 200 km |
381 300 km |
407 000 km |
| rs
|
1,52 108 km |
1,50 108 km |
1,48 108 km |
|
ρ(km) |
104,9 km |
-34,7 km |
- 187,4 km
|
|
ρ(") |
60,5" |
-18,7 |
-94,8 km |
|
σ(km) |
3 379 km |
3 520 km |
3 673 km |
|
σ(") |
1948" |
1901" |
1859" |
| rm-Re
|
305 800 km |
374 900 km |
400 600 km |
|
ρ(km) |
134,1 km
|
-5.0 km |
-157 km |
|
ρ(") |
78,7" |
-2,8" |
-80,8" |
|
σ(km) |
3 350 km |
3 490 km |
3 643 km |
|
σ(") |
1966" |
1918" |
1873" |
Les valeurs extrêmes pour les éclipses périgées et apogées sont en italique et l'on retrouve bien les valeurs des diamètres de 268 km pour une éclipse périgée (donc totale) et de 375 km pour une éclipse apogée (donc annulaire). De même on constate que le diamètre de la pénombre qui est compris entre 6700 km et 7300 km est bien du même ordre de grandeur que deux diamètres lunaires.
Magnitude ou grandeur d'une éclipse de Soleil
Toutes les éclipses de Soleil ne sont pas identiques, il convient donc de trouver un paramètre qui les caractérise, ce paramètre est la grandeur ou la magnitude de l'éclipse, ces deux termes désignent la même quantité.
À un instant donné la grandeur g de l'éclipse est l'inverse du rapport du diamètre du Soleil sur la distance du bord du Soleil le plus rapproché du centre de la Lune au bord de la Lune le plus rapproché du centre du Soleil.
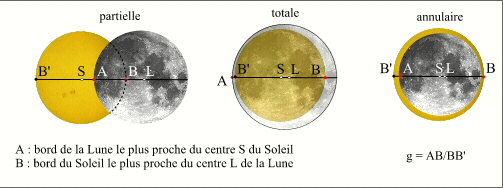
Grandeur ou magnitude d'une éclipses de Soleil.
Crédit : IMCCE/Patrick Rocher
Dans la figure ci-contre, nous avons ajouté une transparence à la Lune dans le cas de l'éclipse totale, cela permet de voir la position du Soleil. Comme on le constate sur la figure, les éclipses partielles et annulaires ont une grandeur inférieure à un et les éclipses totales ont une grandeur supérieure à un. Les éclipses mixtes ont une grandeur très proche de un. Pour les éclipses annulaires, plus la grandeur s'approche de un, plus le diamètre apparent de la Lune est proche du diamètre apparent du Soleil, donc plus l'éclipse est courte. Pour les éclipses totales, plus on s'écarte de un, plus le diamètre apparent de la Lune est grand par rapport au diamètre apparent du Soleil, donc plus l'éclipse est longue.
Degré d'obscuration d'une éclipse
Le degré d'obscuration est aussi un paramètre caractéristique des éclipses de Soleil. Le degré obscuration est le pourcentage de la surface du disque solaire occulté par la Lune.
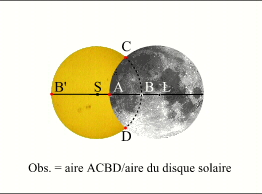
Le degré d'obscuration.
Crédit : IMCCE/Patrick Rocher
Le degré d'obscuration donne une information pour les éclipses annulaires et partielles car sa valeur est inférieure à 100%, par contre toutes les éclipses totales ont un degré d'obscuration de 100% quelle que soit la grandeur de l'éclipse.
La grandeur et le degré d'obscuration sont donnés dans les circonstances générales des éclipses, ce sont alors les valeurs maximales de ces paramètres sur toute la durée de l'éclipse, elles correspondent à un instant et un lieu bien défini sur la Terre : le lieu du maximum de l'éclipse (lieu sur la Terre où la grandeur est maximale) et l'instant où la grandeur est maximale en ce lieu. Ces deux valeurs sont également données dans les circonstances locales des éclipses, dans ce cas elles sont toujours inférieures ou égales (si on est au lieu du maximum) à celles données dans les circonstances générales.
Détermination des types d'éclipses en fonction des positions orbitales
Introduction
 Introduction
Introduction
Après avoir traité de l'aspect purement géométrique des éclipses (tailles et vitesses des cônes d'ombre et de pénombre) dans les sections précédentes, nous avons commencer à faire intervenir les aspects liés aux positions des trois corps. Nous allons dans cette section répondre partiellement à la question, où se trouvent la Lune et le Soleil sur leurs orbites pour qu'une éclipse soit totale, annulaire ou mixte. Dans un premier temps nous raisonnerons sur les diamètres apparents, puis nous verrons une autre approche à partir des distances à la Terre.
Diamètres apparents
En raison des mouvements orbitaux de la Terre et de la Lune, les distances Terre-Lune et Soleil-Terre ne sont pas constantes, les diamètres apparents de la Lune et du Soleil sont donc variables. Le diamètre apparent de la Lune est maximal lorsque la Lune est proche de la Terre donc à son périgée, et il est minimal lorsque la Lune est loin de la Terre donc à son apogée. De même le diamètre apparent du Soleil est maximal lorsqu'il est proche de la Terre donc lorsque le Soleil apparent est à son périgée ou la Terre est à son périhélie (actuellement vers le 4 janvier) et le diamètre apparent du Soleil est minimal lorsque le Soleil est loin de la Terre, donc lorsque le Soleil apparent est à l'apogée ou la Terre à l'aphélie (actuellement vers le 4 juillet).
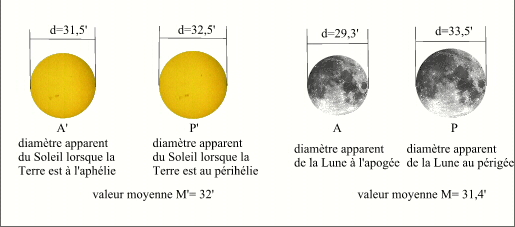
Valeurs extrêmes et moyennes des diamètres apparents du Soleil et de la Lune.
Crédit : IMCCE/Patrick Rocher
Comme on le constate sur la figure ci-contre le diamètre apparent moyen de la Lune est plus petit que le diamètre apparent moyen du Soleil, on peut donc s'attendre à avoir en moyenne plus d'éclipses annulaires que d'éclipses totales.
Positions orbitales
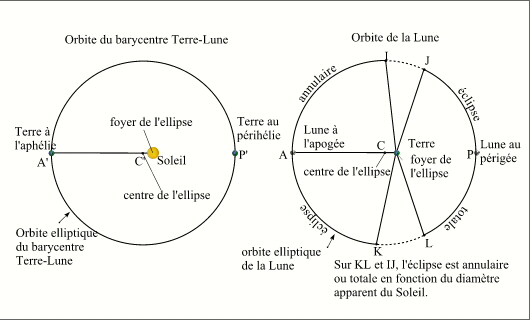
Analyse des types d'éclipses solaire en fonction des positions orbitales de la Terre et de la Lune.
Crédit : IMCCE/Patrick Rocher
Comme nous venons de le voir, nous pouvons calculer les valeurs extrêmes des diamètres apparents de la Lune et du Soleil vus depuis la Terre. Nous allons affiner un peu notre étude, en effet nous pouvons déterminer la portion de l'orbite lunaire sur laquelle le diamètre apparent de la Lune est toujours plus grand que le plus grand diamètre apparent du Soleil (32,5'), c'est l'arc d'orbite LJ sur la figure ci-contre. Sur cette portion d'orbite lunaire les éclipses centrales sont toujours totales, quelle que soit la position de la Terre sur son orbite. Nous pouvons également déterminer la portion de l'orbite lunaire sur laquelle la Lune a un diamètre apparent toujours plus petit que le plus petit diamètre apparent du Soleil (31,5'), c'est l'arc d'orbite IK sur la figure ci-contre. Sur cette portion d'orbite les éclipses centrales sont toujours annulaires quelle que soit la position de la Terre sur son orbite. Sur les portions d'orbites IJ et KL le diamètre apparent de la Lune varie entre 31,5' et 32,5' (valeurs extrêmes du diamètre apparent du Soleil) le type de l'éclipse centrale est donc déterminé par le diamètre apparent du Soleil donc par la position de la Terre sur son orbite. C'est sur ces portions de l'orbite de la Lune que l'on trouve les éclipses mixtes.
On remarquera que sur la figure ci-contre, les orbites de la Terre et de la Lune sont représentées par des cercles, cela est totalement justifié compte tenu des faibles excentricités des orbites lunaire et terrestre. Par contre les corps centraux ne sont pas aux centres des cercles mais sont excentrés. On notera également que l'arc LJ est centré sur le périgée de la Lune, donc les éclipses avec la Lune au périgée sont toujours des éclipses totales, de même l'arc IK est centré sur l'apogée de la Lune donc les éclipses avec la Lune en apogée sont toujours des éclipses annulaires. Enfin l'arc IK est plus grand que l'arc LJ, cela confirme le fait qu'il y ait en moyenne plus d'éclipses annulaires que d'éclipses totales.
Types d'éclipses en fonction des distances des corps
Nous pouvons avoir une autre approche du problème en considérant les distances Soleil-Lune et Lune-Terre, en effet il y a équivalence entre les diamètres apparents et les distances des corps entre eux.
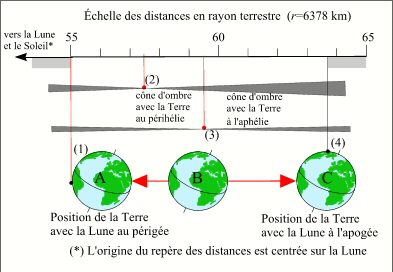
Positions extrêmes pour les éclipses centrales de Soleil.
Crédit : IMCCE/Patrick Rocher
- (1) est la distance observateur-Lune minimale, d=55,0 rayons terrestres, c'est-à-dire avec la Lune au périgée et l'observateur avec la Lune au zénith,
- (4) est la distance observateur-Lune maximale, d=63,8 rayons terrestres, c'est-à-dire avec la Lune à l'apogée et l'observateur avec la Lune à l'horizon,
- (2) correspond à une distance Lune sommet du cône d'ombre de longueur minimale, l=57,5 rayons terrestres, c'est à dire une distance Soleil-Terre minimale donc un Soleil au périgée (ou la Terre au périhélie),
- (3) correspond à une distance Lune sommet du cône d'ombre de longueur maximale, l=59,5 rayons terrestres, c'est-à-dire une distance Soleil-Terre maximale donc un Soleil à l'apogée (ou la Terre à l'aphélie).
Types d'éclipses en fonction des distances des corps-2

Positions extrêmes pour les éclipses centrales de Soleil.
Crédit : IMCCE/Patrick Rocher
Cette figure donne les distances extrêmes de la Terre et du cône d'ombre, en fonction des positions extrêmes de la Lune, du Soleil et de la Terre. L'origine des distances est le centre de la Lune et les distances sont exprimées en rayons terrestres. La distance observateur-Lune varie de 55 à 63,8 rayons terrestres. La distance entre la Lune et le sommet du cône d'ombre varie, elle, de 57 à 59,5 rayons terrestres. Cette figure nous montre que si, au moment de l'éclipse, on est dans la position A, c'est-à-dire avec la Lune au périgée, alors quelle que soit la position de la Terre sur son orbite, l'éclipse est totale car la Terre coupe toujours le cône d'ombre avant son sommet. De même si, au moment de l'éclipse, on est en position C, c'est-à-dire avec la Lune à son apogée, alors quelle que soit la position de la Terre sur son orbite l'éclipse est annulaire car la Terre coupe toujours le prolongement de l'ombre. En faisant varier la position de la Terre (par rapport à la Lune) entre ces deux positions, on peut visualiser tous les cas intermédiaires possibles. Par exemple, lorsque la Terre est en B (distance Lune-Terre = 59 r), si la Terre est au périhélie (cône d'ombre en position 2) l'éclipse est annulaire car la Terre coupe le prolongement du cône d'ombre, si la Terre est à son l'aphélie (cône d'ombre en position 3) alors l'éclipse est totale car la Terre coupe le cône d'ombre, avec un cône d'ombre entre les positions 2 et 3 toutes les configurations sont possibles (éclipses totales, annulaires ou mixtes).
Circonstances générales et cartes des éclipses
Introduction
 Introduction
Introduction
Dans cette section, nous allons décrire les circonstances générales d'une éclipse de Soleil. Ces circonstances représentent l'évolution des contacts et des trajectoires des cônes d'ombres et de pénombres avec la surfaces terrestre. Ces circonstances générales décrivent donc l'évolution de l'éclipse vue par un observateur situé dans l'espace à l'extérieure de la surface terrestre. Nous présenterons ensuite les différentes cartes d'éclipses et les différentes projections qui y sont associées.
Circonstances générales
Les circonstances générales d'une éclipse correspondent aux différentes phases de l'éclipse générale ; ces phases sont les suivantes :
- le commencement et la fin de l'éclipse générale, ce sont les deux instants et les deux lieux sur Terre où le cône de pénombre de la Lune est tangent extérieur à la surface de l'ellipsoïde terrestre,
- le commencement et la fin de l'éclipse totale ou annulaire, ce sont les deux instants et les deux lieux sur Terre où le cône d'ombre de la Lune est tangent extérieur à la surface de l'ellipsoïde terrestre,
- le commencement et la fin de la centralité, ce sont les deux instants et les deux lieux sur Terre où l'axe du cône d'ombre de la Lune est tangent à la surface de l'ellipsoïde terrestre,
- le maximum de l'éclipse, c'est l'instant et le lieu sur Terre où la grandeur de l'éclipse est maximale,
- et l'éclipse centrale à midi ou minuit vrai, c'est l'instant et le lieu sur Terre où le maximum de l'éclipse se produit lorsque le Soleil est dans le plan du méridien. L'éclipse peut effectivement être centrale à minuit vrai, cela arrive lorsque l'éclipse est proche des pôles terrestres, le Soleil passe alors deux fois au méridien par jour à midi vrai et à minuit vrai.
Comme on le constate, ces différentes phases sont liées à l'évolution de l'ombre et de la pénombre à la surface de la Terre, les débuts et fins de chaque phase correspondent à un instant bien particulier et à un lieu unique à la surface du globe terrestre. La différence de temps entre le début et la fin de l'éclipse générale nous donne le temps mis par la pénombre pour parcourir la surface terrestre. De même la différence de temps entre le début et la fin de la phase totale ou annulaire, lorsqu'elles existent, donne le temps mis par l'ombre ou son prolongement pour parcourir la surface terrestre.
En savoir plus: Circonstances générales de l'éclipse des 10 et 11 juin 2002
 En savoir plus
En savoir plus
| Circonstance |
UT |
Longitude |
Latitude |
| Commencement de l'éclipse générale |
le 10 à 20h 51,8m |
-137° 58,5' |
-2° 30,0' |
| Commencement de l'éclipse annulaire |
le 10 à 21h 53,9m |
-120° 51,74 |
+1° 16,0' |
| Commencement de l'éclipse centrale |
le 10 à 21h 54,5m |
-120° 40,8' |
+1° 19,5' |
| Maximum de l'éclipse |
le 10 à 23h 44,3m |
+178° 36,8' |
+34° 32,7' |
| Éclipse centrale à midi ou minuit vrai |
le 10 à 23h 48,2m |
+177° 11,4' |
+34° 55,3' |
| Fin de l'éclipse centrale |
le 11 à 1h 34,0m |
+104° 49,2' |
+19° 48,1' |
| Fin de l'éclipse annulaire |
le 11 à 1h 34,6m |
+104° 59,4' |
+19° 44,9' |
| Fin de l'éclipse générale |
le 11 à 2h 36,6m |
+122° 15,8' |
+16° 1,0' |
Dans ce tableau les longitudes sont comptées positivement vers l'ouest et négativement vers l'est. On remarquera que l'éclipse se déplace d'ouest en est et du sud vers le nord. On donne toujours les instants des différentes phases des éclipses en Temps universel coordonné, cela évite les problèmes liés aux heures locales. Dans notre exemple, l'éclipse est à cheval sur deux jours en temps universel coordonné, le 10 et le 11 juin 2002.
La phase annulaire débute le 10 juin à 21h 53,9m UTC en un point de longitude -120° 51,7' (est) et de latitude 1° 16,0' (nord), ce lieu se trouve à l'est en Indonésie (au nord des Célèbes), la phase annulaire se termine le 11 juin à 1h 34,6m UTC en un point de longitude +104° 59,4' (ouest) et de latitude +19° 44,9' (nord), ce lieu se trouve sur la côte ouest du Mexique. Si l'on exprime ces instants en heures locales, le début de la phase annulaire, en Indonésie est le 10 juin à 21h 53,9m + 8h = 29h 53,9m soit le 11 juin à 5h 53,9m temps légal en Indonésie, donc le 11 juin 2002 au matin, et la fin de la phase annulaire, au Mexique est le 11 juin à 1h 34,6m - 7h = -5h 25,4m = 18h 34,6m le 10 juin en temps légal au Mexique, donc le 10 juin 2002 au soir. On a donc la phase annulaire qui commence le matin du 11 juin 2002 en Indonésie et se termine le soir du 10 juin au Mexique, elle se termine donc en temps légal avant d'avoir commencé, ce qui est normal car la bande de centralité traverse la ligne de changement de date d'ouest en est donc on perd un jour en temps légal.
L'usage systématique du Temps universel évite ces paradoxes temporels pour les éclipses franchissant la ligne de changement de date, néanmoins l'observateur, lors de ses déplacements doit tenir compte des passages en heures légales s'il ne veut pas arriver un jour trop tard pour son observation !
Les cartes d'éclipses
On distingue deux types de cartes, les cartes générales et les cartes locales.
Pour chaque éclipse, on trace généralement une ou deux cartes générales de l'éclipse. Sur ces cartes on fait figurer les courbes suivantes : la bande de centralité (lorsqu'elle existe), les limites boréale et australe de l'éclipse, les courbes de commencement, de fin et de maximum au lever et au coucher du Soleil, ainsi que les courbes de commencement et fin pour des instants donnés (toutes les heures en général). Pour le tracé de ces cartes, on utilise une projection stéréographique, c'est-à-dire une projection azimutale conforme. Cette projection, qui conserve les angles mais pas les distances, déforme les continents mais permet d'avoir une représentation des pôles terrestres sur la carte. On utilise également une projection orthographique, elle permet de représenter la trajectoire de l'éclipse sur un globe terrestre vu de l'espace.
On trace également, un certain nombre de cartes locales. Sur ces cartes, on donne également les courbes de commencement, de fin et de maximum pour des instants donnés (avec un pas plus adapté à la carte), et parfois on trace aussi la projection de l'ombre pour des instants donnés. Les cartes locales sont tracées à l'aide de différentes projections en fonction des lieux représentés (projection conforme de Lambert, projection de Mercator...).
En savoir plus: Exemple de carte générale en projection stéréographique
 En savoir plus
En savoir plus
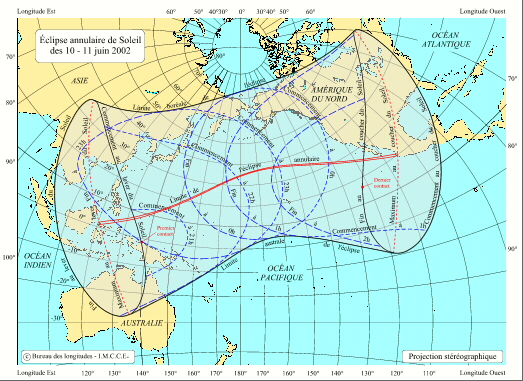
Carte générale de l'éclipse des 10 - 11 juin 2002
Crédit : IMCCE/Patrick Rocher
Sur cette carte on a tracé la bande de centralité (en rouge), les limites boréale et australe de l'éclipse, ce sont les limites boréale et australe du cône de pénombre durant l'éclipse. On donne également les limites du cône de pénombre toutes les heures (commencement et fin à un instant donné, courbes bleues) et les lieux des commencements, maxima et fins d'éclipse au lever et au coucher du Soleil (courbes noires et rouges joignant les extrémités des limites boréale et australe de l'éclipse). On notera la différence de taille entre la surface terrestre où l'éclipse est visible sous la forme d'une éclipse partielle (surface grisée) et la surface de la bande de centralité.
Des cartes plus grandes, et plus lisibles, sont disponibles sur le serveur de l'IMCCE.
En savoir plus: Exemple de carte en projection orthographique
 En savoir plus
En savoir plus
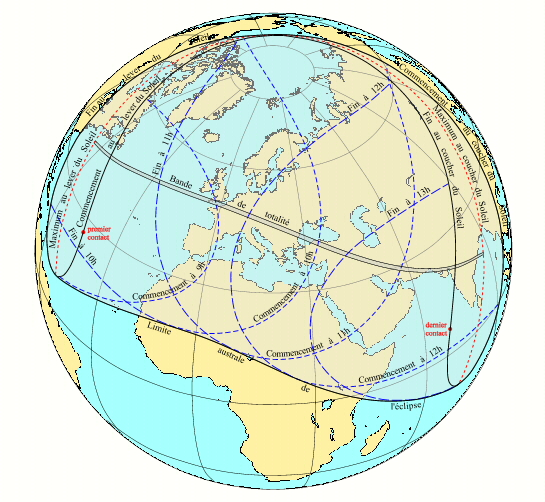
Projection orthographique de l'éclipse du 11 août 1999.
Crédit : IMCCE/Patrick Rocher
La projection orthographique permet de représenter l'éclipse générale sur la Terre, vue depuis l'espace. Les courbes représentées sont les mêmes que dans la représentation stéréographique.
En savoir plus: Exemple de carte locale
 En savoir plus
En savoir plus
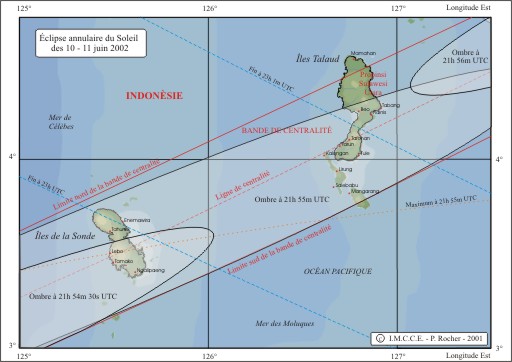
Carte locale de l'éclipse des 10 - 11 juin 2002 sur l'Indonésie.
Crédit : IMCCE/Patrick Rocher
Cette carte locale en projection de Lambert donne le tracé de la ligne de centralité sur une partie de l'Indonésie, les deux îles de cette carte sont les deux seuls lieux terrestres où la phase annulaire de l'éclipse fut observable. On a également tracé l'intersection du prolongement du cône d'ombre avec la surface terrestre. Comme on est en début d'éclipse, on notera l'aspect très allongé de la projection.
En savoir plus: Les différentes projections
 En savoir plus
En savoir plus
On peut classer les projections géographiques en fonction des propriétés géométriques des projections des parallèles et des méridiens d'une sphère. On entend par méridiens les grands cercles passant par le pôle de projections et par parallèles les cercles intersections de la sphère et des plans normaux à la direction des pôles.
Une projection est dite :
- méricylindrique si et seulement si le méridien central est une droite (ou un segment), si les parallèles sont des droites (ou des segments, éventuellement des points) perpendiculaires au méridien central, et si les méridiens des courbes coupent les parallèles à intervalles réguliers.
- cylindrique si et seulement si elle est méricylindrique et si les méridiens sont des droites parallèles entre elles.
- polyconique si et seulement si le méridien central est une droite, si les parallèles sont des arcs de cercles dont les centres sont sur le méridien central et si les méridiens des courbes coupent les parallèles à intervalles réguliers.
- mériconique si et seulement si elle est polyconique et si les parallèles sont concentriques.
- tronconique si et seulement si elle est mériconique et si les méridiens sont des droites qui se coupent au centre des parallèles.
- conique si et seulement si elle est tronconique et si un des pôle est ponctuel (par pôle on entend un point de latitude +/-90°).
- azimutale (ou zénithale) si et seulement si elle est conique et si les parallèles sont des cercles complets.
Une projection à partir d'un centre de projection sur une surface quelconque, suivie d'un développement de cette surface s'appelle une projection perspective. par exemple les projections cylindriques et coniques sont des projections perspectives.
Les projections sont également classées en fonction des propriétés qu'elles conservent. On distingue donc de projections :
- Équivalentes
: lorsque qu'il y a conservation des aires.
- Conformes : lorsqu'il y a conservation locale des angles, donc les formes.
- Équidistantes : lorsqu'il y a conservation des distances sur les méridiens.
- Équidistantes : lorsqu'il y a conservation les distances sur les méridiens (la conservation de toutes les distances n'étant pas possible).
- Orthodromiques : lorsqu'un un grand cercle de la sphère est représenté par une droite, alors le plus court chemin entre deux points est un segment de droite sur la carte. Ceci est utile en navigation (beaucoup de cartes marines utilisent cette projection).
- Loxodromiques : lorsque les courbes d'azimut constant sont des droites (ou des segments de droite). Cette propriété découle directement de la conformité et du fait que les méridiens sont des droites parallèles.
- Transverse : lorsque l'on intervertit le rôle des latitudes et des longitudes.
Les autres projections sont dites aphylactiques.
Quelques exemples :
- La projection de Mercator est une projection cylindrique conforme et elle est loxodromique.
- La projection stéréographique, appelée également projection gnomonique, est une projection azimutale conforme, elle est orthodromique.
- La projection orthogonale, appelée également projection orthographique, est une projection azimutale conforme.
Circonstances locales des éclipses
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire les circonstances locales d'une éclipse. C'est-à-dire ce que voit un observateur à la surface de la Terre. Dans ce cas on regarde le Soleil et la Lune (et non la Terre et l'ombre de la Lune). L'observateur en fonction de sa position, verra ou ne verra pas d'éclipses. Dans le cas d'une éclipse centrale, suivant sa position, il verra la phase centrale ou non.
La partie pour en savoir plus est complexe et demande une bonne connaissance du calcul numérique.
Circonstances locales éclipses totales
Il ne faut pas les confondre avec les circonstances générales décrites dans le paragraphe précédent. Les circonstances locales d'une éclipse décrivent, en un lieu donné, les différentes phases de l'éclipse, observables par un observateur situé en ce lieu.
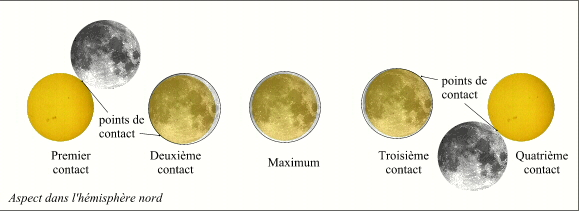
Phases locales d'une éclipse totale.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de totalité durant une éclipse totale de Soleil, pour rendre le dessin plus lisible nous avons ajouté une transparence à la Lune durant la totalité pour permettre de voir la position du Soleil occulté par la Lune. La durée de la phase de totalité en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase totale) est égale à l'intervalle de temps séparant les premier et quatrième contacts. Les points de Baily apparaissent au voisinage des deuxième et troisième points de contacts.
Circonstances locales éclipses annulaires
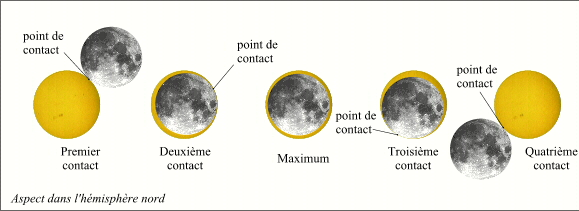
Phases locales d'une éclipse annulaire.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de centralité d'une éclipse annulaire. La durée de la phase annulaire en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase annulaire) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Circonstances locales éclipses partielles

Phases locales d'une éclipse partielle.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé sur le trajet du cône de pénombre d'une éclipse. L'éclipse peut être partielle, annulaire ou totale. Dans les deux derniers cas, l'observateur n'est pas dans la bande de centralité, il observe donc l'éclipse annulaire ou totale sous la forme d'une éclipse partielle. La durée de l'éclipse locale (phase partielle) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Ces phases sont les suivantes :
- le début de l'éclipse partielle, appelé également premier contact (parfois premier contact extérieur),
- le début de l'éclipse totale ou annulaire (si l'observateur est dans la bande de centralité), appelé également deuxième contact (parfois premier contact intérieur),
- le maximum de l'éclipse, instant où la grandeur est maximum en ce lieu,
- la fin de l'éclipse totale ou annulaire (si l'observateur est dans la ligne de centralité), appelée également troisième contact (parfois deuxième contact intérieur),
- la fin de l'éclipse partielle, appelée également quatrième contact (parfois deuxième contact extérieur).
Circonstances locales angles au pole et au zenith
Pour chacun des contacts, en plus des instants du contact, on donne à l'observateur l'angle au pôle
P et l'angle au zénith Z. On remarquera que les points des contacts intérieurs des éclipses totales sont diamétralement opposés aux points des contacts intérieurs des éclipses annulaires.
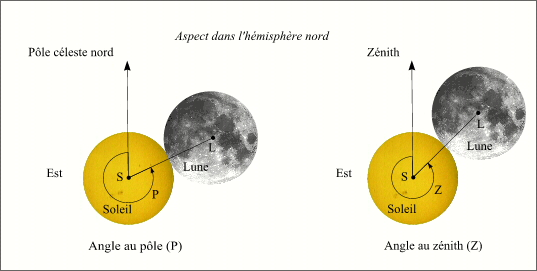
Définitions des angles au pôle et au zénith
Crédit : IMCCE/Patrick Rocher
L'angle au pôle P d'un contact est l'angle de la direction nord N (partie boréale du cercle horaire du centre S du Soleil) avec l'arc de grand cercle joignant les centres S et L du Soleil et de la Lune, compté positivement vers l'est, dans le sens nord-est-sud-ouest.
L'angle au zénith Z d'un contact a une définition analogue à celle de P, en remplaçant le cercle horaire du centre S du Soleil par le vertical du même point.
Circonstances locales-5
 Remarques
Remarques
Sous nos latitudes (en France) et pour les latitudes positives situées au-dessus du tropique du Cancer (latitudes supérieures à 23°), le Soleil passe au méridien au sud, donc quand on regarde le Soleil, l'ouest est à droite du Soleil et l'est est à sa gauche. La Lune éclipse le Soleil d'ouest en est (donc de la droite vers la gauche lorsque l'on regarde le Soleil). Pour les latitudes négatives situées sous le tropique du Capricorne (latitudes inférieures à -23°), le Soleil passe au méridien au nord, l'aspect du phénomène est inversé, l'éclipse a, bien évidemment, toujours lieu d'ouest en est, mais elle a lieu de la gauche vers la droite car on regarde le Soleil vers le nord. Dans la zone intertropicale les deux cas de figure sont possibles, cela dépend de la date de l'éxclipse et du lieu d'observation. La connaissance des instants et positions du deuxième et du troisième point de contact est très importante pour les éclipses totales de Soleil, car elle indique quand et où vont apparaître les points de Baily.
Avec l'instant du maximum on donne également la grandeur de l'éclipse, le degré d'obscuration, la hauteur h et l'azimut a du Soleil.
La hauteur h du Soleil sur l'horizon est l'angle de la direction du Soleil et du plan horizontal, compté en degrés de -90° à +90°.
L'azimut est l'angle formé par la projection de la direction du Soleil dans le plan horizontal avec la direction du Sud, compté en degré dans le sens rétrograde (sud = 0°, ouest = 90°, nord = 180°, est = 270°).
Les circonstances locales d'une éclipse peuvent être calculées à l'aide des éléments de Bessel
En savoir plus: Définition des éléments de Bessel
 En savoir plus
En savoir plus
Au XIXe siècle, l'astronome allemand Friedrich Bessel (1784-1846) a mis au point une méthode, toujours utilisée de nos jours, pour faciliter le calcul des circonstances locales et générales d'une éclipse de Soleil.
Pour un lieu donné il y a lieu de déterminer :
- les instants des différents contacts,
- l'instant du maximum de l'éclipse et la grandeur de l'éclipse à cet instant,
- les angles au pôle et au zénith de chacun des contacts.
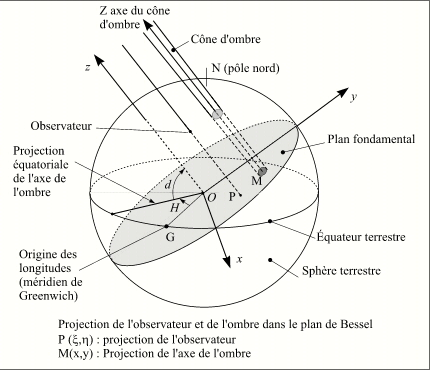
Les éléments de Bessel.
Crédit : IMCCE/Patrick Rocher
Le lieu d'observation est défini par sa longitude λ (positive à l'ouest et négative à l'est du méridien de Greenwich), sa latitude ϕ et son altitude h au-dessus du niveau de la mer.
On définit à chaque instant un système de coordonnées Oxyz de sens direct, dans lequel :
O est le centre de la Terre.
L'axe Oz est parallèle à l'axe des cônes de pénombre et d'ombre, le sens positif étant celui qui va de la Terre à la Lune.
L'axe Ox est l'intersection du plan fondamental Oxy perpendiculaire à Oz et du plan de l'équateur terrestre, le sens positif étant vers l'est.
L'axe Oy est normal à Ox dans le plan fondamental, le sens positif étant vers le nord.
En savoir plus: Définition des éléments de Bessel-2
 En savoir plus
En savoir plus
En utilisant comme unité de longueur le rayon équatorial terrestre, les éléments de Bessel sont définis de la manière suivante :
x, y, z sont les coordonnées du centre de la Lune.
d et H sont la déclinaison de l'axe Oz et son angle horaire par rapport au méridien de Greenwich.
fe et fi sont les demi-angles au sommet des cônes de pénombre et d'ombre, fe étant pris par convention positif et fi négatif.
ue et ui sont les rayons des sections circulaires des cônes de pénombre et d'ombre par le plan fondamental Oxy et s'obtiennent par les formules suivantes :
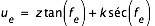
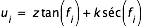
où k est le rayon de la Lune exprimé en rayon équatorial terrestre.
En savoir plus: Définition des éléments de Bessel-3
 En savoir plus
En savoir plus
Les coordonnées ξ, η, ζ du lieu d'observation dans le système Oxyz sont :
ξ = ρ . cos ϕ ' . sin (H - λ ),
η = ρ . sin ϕ ' . cos d - ρ . cos ϕ ' . sin d . cos ( H - λ ),
ζ = ρ . sin ϕ ' . sin d + ρ . cos ϕ ' . cos d . cos ( H - λ ),
avec :
ρ . cos ϕ ' = cos u + h/r0 . cos ϕ
ρ . sin ϕ ' = (1 - f) . sin u + h/r0 . sin ϕ
et
tan u = (1 - f) . tan ϕ
où h est l'altitude du lieu exprimée en mètres, r0 est le rayon équatorial terrestre exprimé en mètres et f l'aplatissement de l'ellipsoïde terrestre (f = 1/298,257 = 0,003 35281).
En savoir plus: Définition des éléments de Bessel-4
 En savoir plus
En savoir plus
Les variations horaires ξ ', η ', ζ ' de ces coordonnées sont fournies avec une précision de l'ordre de la seconde de temps par les formules suivantes, H' étant exprimé en radians par heure.
ξ ' = H' . ρ . cos ϕ ' . cos (H - λ ),
η ' = H' . ξ . sin d,
ζ ' = - H' . ξ . cos d,
Les rayons le et li des sections circulaires des cônes de pénombre et d'ombre par le plan mené par le lieu d'observation parallèlement au plan fondamental s'obtiennent par les formules suivantes :
le =ue - ζ tan fe
li = ui - ζ tan fi
En savoir plus: Calcul des circonstances locales
 En savoir plus
En savoir plus
Chaque élément de Bessel que l'on pourra désigner par b est représenté sur un intervalle de temps (t0, t1) par des coefficients de développements en polynômes du temps, à l'exception de tan fe et de tan fi qui sont considérées comme constantes sur l'intervalle. Un élément de Bessel se calcule à un instant t par la formule :
b = b0 + b1 . T + b2 . T2 + b3 . T3
avec T = t - t0.
T, exprimé en heure, représente le temps écoulé depuis l'instant origine t0.
La variation horaire b' d'un élément de Bessel se calcule par la formule :
b' = b1 + 2 b2 . T + 3 b3. T2
En savoir plus: Calcul de la grandeur maximale en un lieu
 En savoir plus
En savoir plus
Soient :
U = x - ξ , U' = x' - ξ',
V = y - η , V' = y' - η ',
On prend comme valeur de départ td l'époque du maximum de l'éclipse, l'instant du maximum tm se calcule en ajoutant à td la valeur Dtm donnée par :
Dtm = - (UU' + VV') / (U'2+ V'2)
On doit réitérer le calcul en prenant comme nouvelle valeur de départ la valeur de tm.
La grandeur maximale est donnée par :
g = (le - lm) / (le - li)
pour une éclipse annulaire ou totale au lieu considéré, où :
g = (le - lm) / (2 le- 0,5465) pour une éclipse partielle, avec :
lm = (U2 + V2)1/2
En savoir plus: Calcul des instants des contacts en un lieu
 En savoir plus
En savoir plus
On prend comme valeurs de départ td du premier et du quatrième contacts (contacts extérieurs) des valeurs approchées déduites de la carte de l'éclipse et l'on prend comme valeurs de départ du second et du troisième contacts (contacts intérieurs), lorsqu'ils existent, la valeur tm du maximum calculée précédemment.
Pour chaque valeur td de départ on calcule les quantités suivantes :
β = (UU' + VV') / (U'2 + V'2),
γ = (U2 + V2 - l2) / (U'2 + V'2),
θ = ±(β2 - γ)1/2
avec l = le ou l = li et θ étant du signe de β.
Les instants du premier et du quatrième contacts se calculent par la formule :
t = td - β + θ
et les instants du second et du troisième contacts se calculent par les formules :
t = td - β - |θ| pour le second contact,
et
t = td - β + |θ| pour le troisième contact.
Comme pour le calcul du maximum on doit réitérer les calculs en prenant comme nouvelles valeurs de départ les valeurs t.
En savoir plus: Calcul de l'angle au pôle et de l'angle au zénith
 En savoir plus
En savoir plus
La valeur de l'angle au pôle P d'un point de contact est donnée par :
tan P = U/V ,
où sin P a le signe de U, sauf pour les second et troisième contacts (contacts intérieurs) d'une éclipse totale pour lesquels sin P est de signe contraire à U.
L'angle au zénith Z d'un point de contact est donné par :
Z = P - Γ ,
en désignant par Γ l'angle parallactique défini d'une façon approchée par :
tan Γ = ξ/η ,
sin Γ étant du signe de ξ.
Visibilité des éclipses de Soleil
Auteur: P. Rocher - IMCCE - Observatoire de Paris
Introduction
 Introduction
Introduction
Après avoir étudié la géométrie des éclipses de Soleil, nous allons répondre à la question : quand ont lieu les éclipses de Soleil? Pour cela nous allons définir la ligne des noeuds de l'orbite lunaire et nous allons étudier son mouvement.
 Prérequis
Prérequis
Les éclipses de Soleil.
Quand ont lieu les éclipses de Soleil ?
Introduction
 Introduction
Introduction
Dans cette section nous définissons la ligne des noeuds de l'orbite lunaire et nous étudions son déplacement angulaire moyen dans le plan de l'écliptique. Puis, nous définissons la fréquence avec laquelle le Soleil apparent passe dans la direction de la ligne des noeuds (la saison des éclipses).
Nous définissons ensuite un critère portant sur la latitude de la Lune au moment de sa conjonction avec le Soleil, pour savoir s'il y a ou non une éclipse de Soleil. Nous donnons les bornes de ce critère en fonction du type d'éclipse observable.
Enfin nous transposons ce critère sur la latitude lunaire en un critère sur la différence de longitude entre la longitude de la conjonction et la longitude du noeud lunaire.
Les parties pour en savoir plus vous montre comment calculer la valeur moyenne de la saison d'éclipse, puis nous explique le mouvement réelle de cette ligne. Nous donnons également la démonstration des critères en latitude.
Le mouvement moyen de la ligne des noeuds
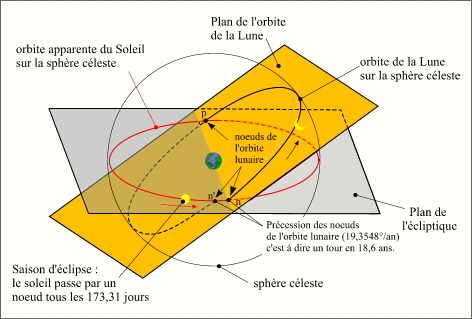
Orbite de la Lune, mouvement de la ligne des noeuds.
Crédit : IMCCE/Patrick Rocher
Il y a éclipse de Soleil lorsque la Terre passe dans le cône d'ombre ou dans le cône de pénombre de la Lune. Le Soleil, la Lune et la Terre sont alors presque alignés, et on est au voisinage de la nouvelle Lune (conjonction). Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Soleil à chaque nouvelle Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 17' sur le plan de l'orbite terrestre à la nouvelle Lune. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l'orbite de la Lune sont appelées noeuds de l'orbite lunaire.
Le mouvement moyen de la ligne des noeuds-2
Cette ligne des noeuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans, soit un déplacement moyen de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc, dans le repère écliptique géocentrique, que la direction Terre-Soleil soit près de la ligne des noeuds lunaires au moment de la nouvelle Lune. Compte tenu du mouvement moyen de précession des noeuds, le Soleil apparent passe en moyenne par l'un des deux noeuds tous les 173,31 jours. Cette période porte le nom de saison des éclipses. Il passe par le même noeud tous les 346,62 jours, cette période porte le nom d'année des éclipses.
En savoir plus: Le calcul de la saison des éclipses
 En savoir plus
En savoir plus
La direction Terre-Soleil est la direction du Soleil apparent vu depuis la Terre, elle fait donc 360° pendant une révolution sidérale de la Terre. La ligne des noeuds de l'orbite lunaire se déplace en moyenne de 19,3413618°/an dans le sens rétrograde. On a donc deux mouvements en sens contraire. La période T qui ramène le Soleil apparent dans la direction d'un même noeud de l'orbite lunaire est solution de l'équation suivante :
T . 360°/an + T . 19,3413618°/an = 360°
ce qui donne T = 360/(360 + 19,3413618) an = 0,9490133 an.
L'année sidérale étant égale à : an = 365,2563632 jours, T = 346,63 jours.
La saison des éclipses correspond à l'intervalle de temps mis par le Soleil apparent pour passer d'un noeud de l'orbite lunaire à l'autre, elle est donc égale à T/2 ~ 173,31 jours.
La valeur de cette période T nous permet de calculer la vitesse moyenne du Soleil apparent (ou de la Terre) dans un repère tournant lié à la ligne des noeuds de l'orbite lunaire. Par rapport à cette ligne des noeuds le Soleil apparent fait un tour de 360° en 346,63 jours, sa vitesse moyenne par rapport à la ligne des noeuds est donc de 360°/346,63j = 1,038°/jour.
En savoir plus: Le mouvement réel de la ligne des noeuds
 En savoir plus
En savoir plus
En réalité, le mouvement rétrograde de la ligne des noeuds présente des inégalités importantes. À certaines époques, sa vitesse est le double de la moyenne. À d'autres moments, sa vitesse est presque nulle, les noeuds sont alors quasi stationnaires. Cela se produit aux voisinages du passage du Soleil dans la direction de la ligne des noeuds, donc au voisinage des éclipses de Soleil (et aussi de Lune). On peut expliquer ce phénomène de la manière suivante, lorsque le Soleil est sur la ligne des noeuds, il se trouve dans le plan de l'orbite de la Lune, la force perturbatrice du Soleil est alors comprise dans le plan de l'orbite de la Lune, donc la composante perpendiculaire à ce plan est nulle et ne "tire" pas sur le plan de l'orbite. Le fait que les noeuds soient quasi-stationnaires au moment des éclipses est très important, en effet les positions moyennes des noeuds sont alors presque égales aux positions vraies, donc dans l'étude des éclipses on peut utiliser le mouvement moyen des noeuds.
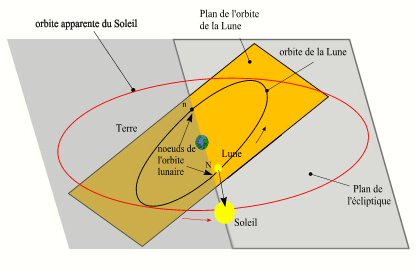
Système Terre - Lune - Soleil lorsque le Soleil est sur la ligne des noeuds
Crédit : IMCCE/Patrick Rocher
Le critère en latitude
On démontre qu'une éclipse de Soleil se produira si, au moment de la nouvelle Lune (instant où les longitudes géocentriques de la Lune et du Soleil sont égales, c'est-à-dire au moment de la conjonction en longitude), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du Soleil est inférieure à 1,41° (1° 24' 37"), elle se produira peut-être si elle est comprise entre 1,41° (1° 24' 37") et 1,58° (1°34' 46") et elle ne se produira pas si elle est supérieure à 1,58° (1° 34' 46").
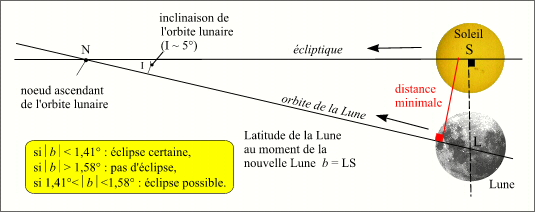
Critères en latitude pour les éclipses de Soleil (vu depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-contre, la distance minimale correspond à l'instant où pour un observateur terrestre, le centre de la Lune est le plus près possible du centre du Soleil, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Soleil on a toujours un des deux scénarii suivants :
- si l'éclipse a lieu avant le passage de la Lune au noeud, on observe d'abord la conjonction (nouvelle Lune), puis le maximum de l'éclipse, puis le passage au noeud,
- si l'éclipse a lieu après le passage de la Lune au noeud, on observe d'abord le passage au noeud, puis le maximum de l'éclipse et enfin la conjonction.
La géométrie de ce dessin montre également que plus la conjonction est proche du noeud, plus la distance minimale entre la Lune et le Soleil est petite et plus la magnitude de l'éclipse est grande. Ainsi, les éclipses partielles correspondent à des conjonctions situées loin des noeuds de l'orbite lunaire et les éclipses centrales (annulaires, totales ou mixtes) correspondent à des conjonctions proches des noeuds de l'orbite lunaire. On rappelle que le fait qu'une éclipse centrale soit annulaire, totale ou mixte ne dépend pas de la distance de la conjonction aux noeuds de l'orbite lunaire, mais dépend uniquement des tailles des diamètres apparents des corps, donc de leurs positions sur leur orbite.
Les bornes du critère en latitude
On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,88°) on a une éclipse centrale avec certitude et pour quelle valeur de b (1,05°) on n'a pas d'éclipse centrale avec certitude (mais une éclipse partielle avec certitude), ces valeurs sont données dans le graphique ci-contre.
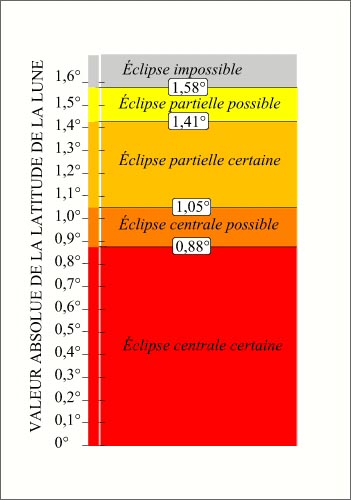
Crédit : IMCCE/Patrick Rocher
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Soleil il faut que b soit inférieure à  = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
En savoir plus: La parallaxe solaire et la parallaxe lunaire
 En savoir plus
En savoir plus
La démonstration du critère en latitude fait intervenir la notion de parallaxe équatoriale solaire et de parallaxe équatoriale lunaire, il convient donc de les définir.
La parallaxe équatoriale solaire est égale à l'angle sous lequel un observateur situé au centre du Soleil voit le rayon terrestre, de même la parallaxe équatoriale lunaire est l'angle sous lequel un observateur situé au centre de la Lune voit le rayon terrestre. C'est également la différence angulaire sous laquelle deux observateurs, l'un situé au centre de la Terre, l'autre situé sur la Terre et observant la Lune à l'horizon, voient le centre de la Lune.
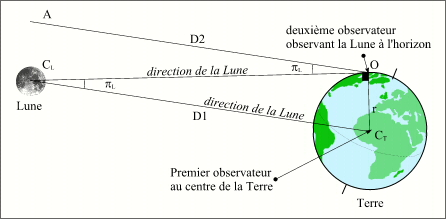
La parallaxe équatoriale lunaire
Crédit : IMCCE/Patrick Rocher
Comme on le constate sur la figure, les deux droites D1 et D2 étant parallèles les angles AOCL et OCLCT sont des angles alternes internes, donc égaux. Ainsi, si les éphémérides donnent une direction angulaire géocentrique de la Lune b, un observateur qui regarde la Lune à l'horizon, la voit dans la direction b -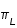 .
.
La parallaxe se calcule par la formule : 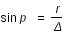 ,
, 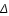 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
En savoir plus: La démonstration du critère en latitude
 En savoir plus
En savoir plus
Nous allons établir le critère en latitude dans le cas d'une éclipse au noeud ascendant de l'orbite lunaire, la conjonction ayant lieu avant le passage au noeud. La démonstration est identique pour un passage au noeud descendant ou avec une conjonction située après le passage au noeud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
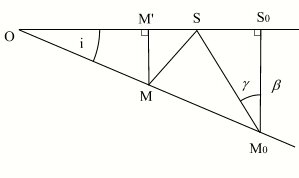
Critère en latitude
Crédit : IMCCE/Patrick Rocher
Soit M0 et S0 : les positions de la Lune et du Soleil à l'instant de la conjonction (nouvelle Lune) avant le passage de la Lune au noeud ascendant de son orbite.
M et S : les positions de la Lune et du Soleil à un instant t postérieur à la conjonction.
 : l' angle S0M0S.
: l' angle S0M0S.
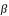 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
q : rapport du mouvement en longitude de la Lune sur celui du Soleil.
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM (corrigé des parallaxes équatoriales lunaire et solaire) et de le comparer avec la somme des demi-diamètres apparents du Soleil et de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore.
En savoir plus: Critère en latitude-3
 En savoir plus
En savoir plus
On a :
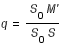 soit
soit 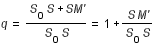
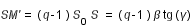 avec
avec 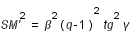
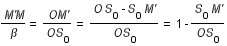
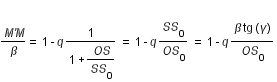
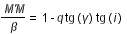
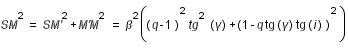 (1)
(1)
On introduit un angle auxiliaire i', tel que : 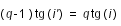
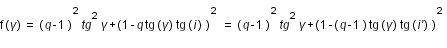
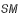 est minimum lorsque
est minimum lorsque 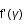 la dérivée de f est nulle
la dérivée de f est nulle
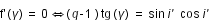 (2)
(2)
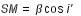 (3)
(3)
En savoir plus: Critère en latitude-4
En savoir plus: Critère en latitude-5
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.
Valeurs extrêmes et moyennes des paramétres
| Paramètres |
Maximum |
Minimum |
Moyenne |
| q |
16,2 |
10,9 |
13,5 |
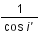
|
1,0052 |
1,0043 |
1,00472 |
Parallaxe de la Lune 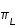
|
61' 27" |
53' 53" |
57' 2,70" |
Parallaxe du Soleil 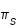
|
8,96" |
8,65" |
8,80" |
Demi-diamètres de la Lune 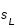 |
16' 45" |
14' 41" |
15' 32,58" |
Demi-diamètres du Soleil 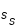
|
16' 18" |
15' 46" |
15' 59,63" |
Valeurs extrêmes et moyennes des paramètres.
En savoir plus: Critère en latitude-6
 En savoir plus
En savoir plus
Le critère en latitude s'écrit donc :
si 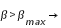 pas éclipse
pas éclipse
si 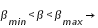 éclipse possible
éclipse possible
si 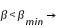 éclipse certaine
éclipse certaine
Si l'on utilise les paramètres du tableau précèdent on trouve 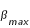 = 1° 34' 45,69" et
= 1° 34' 45,69" et 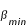 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 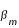 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
Le critère pour la centralité se calcule d'une manière analogue, il suffit de remplacer la somme des demi-diamètres apparents par la différence des demi-diamètres apparents dans l'équation (5). On obtient alors 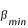 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 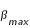 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 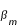 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).
Critère en longitude
Le critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude de la conjonction Lune Soleil (donc la longitude) du Soleil par rapport au noeud de l'orbite lunaire. Ainsi il y aura éclipse si au moment de la conjonction en longitude, la différence de longitude entre le noeud de l'orbite lunaire et la longitude du Soleil est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit le critère en longitude est beaucoup plus large en amplitude que le critère en latitude, cela s'explique par la faible valeur de l'inclinaison de l'orbite lunaire.
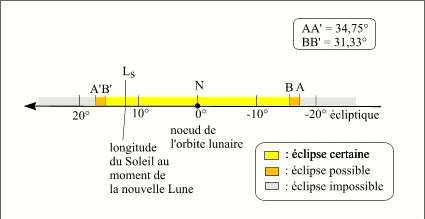
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
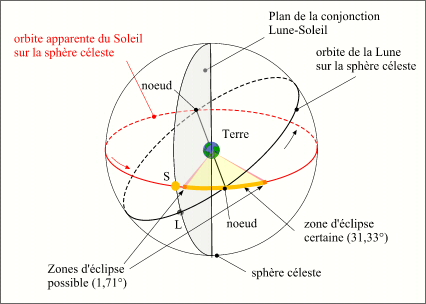
Critère en longitude pour les éclipses de Soleil (vu depuis l'espace)
Crédit : IMCCE/Patrick Rocher
Nombres d'éclipses de Soleil ?
Introduction
 Introduction
Introduction
Maintenant que nous avons défini des critères en latitude ou en longitude pour savoir s'il y a ou non des éclipses de Soleil, nous verrons qu'il y a obligatoirement ou moins une éclipse de Soleil à chaque saison d'éclipse et qu'il en est de même pour les éclipses de Lune. Nous donnons ensuite le nombre d'éclipses possibles sur une année solaire de 365 ou 366 jours.
Enfin nous étudions l'évolution du type des éclipses qui se succèdent d'une saison d'éclipse à la suivante. Pour compléter cette étude nous donnons et commentons un graphique représentant toutes les éclipses de Lune et de Soleil sur une période de 22 ans.
Nombre d'éclipses à chaque saison d'éclipses
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
En étudiant la figure ci-contre, on peut se poser la question suivante. Supposons que nous ayons une conjonction en longitude (1) juste avant le point A, la conjonction suivante (2) va-t-elle être à l'intérieur ou à l'extérieur de l'arc BB' ? Pour répondre à cette question, on doit calculer de combien avance la longitude de la Terre (ou du soleil apparent) par rapport au noeud de l'orbite lunaire durant une révolution synodique de la Lune (une lunaison). On a vu que la Terre (ou le Soleil apparent) passe par le même noeud de l'orbite lunaire tous les 346,62 jours, donc la vitesse de la Terre par rapport à la ligne des noeuds est de 360°/346,64jours = 1,0386°/jour. Or la révolution synodique moyenne de la Lune est de 29,53 jours, donc entre deux conjonctions consécutives la longitude de la Terre varie de 1,0386 x 29,53 = 30,67°.
Or cette valeur est inférieure à la valeur de l'arc qui est égale à 31,33°. Donc à chaque passage de la Terre (ou du soleil apparent) par un noeud de l'orbite lunaire il y a obligatoirement une éclipse de Soleil au voisinage de la conjonction dont la longitude est la plus proche du noeud de l'orbite lunaire.
Nombre d'éclipses à chaque saison d'éclipses-2
Au moins deux éclipses (Lune et Soleil)
On peut donner une information supplémentaire, comme le critère en longitude est le même pour les éclipses de Lune, une demi-lunaison avant ou après la conjonction (nouvelle Lune) la Lune est en opposition (pleine Lune) et la Terre n'a parcouru que 15,335° en longitude par rapport au noeud, ces 15,335° correspondent à l'écart angulaire entre une conjonction et une opposition. Donc si une conjonction se trouve dans l'arc BB' l'opposition suivante ou l'opposition précédente se trouve obligatoirement aussi sur cet arc et il y a une éclipse de Lune, mais à l'autre noeud de l'orbite lunaire.
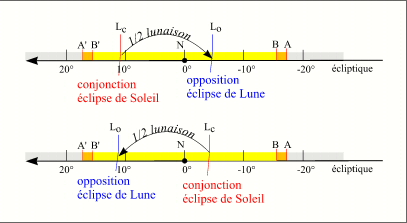
Conjonction et opposition au voisinage du noeud
Crédit : IMCCE/Patrick Rocher
À chaque saison d'éclipse, il y obligatoirement deux éclipses, une éclipse de Soleil et une éclipse de Lune.
Nombre d'éclipses à chaque saison d'éclipses-3
Au plus trois éclipses (Lune et Soleil)
La variation de longitude de la Terre par rapport à la ligne des noeuds durant une lunaison étant de 30,67° et l'arc BB' ayant une longueur de 31,33°, il est également possible d'avoir deux conjonctions contenues dans l'arc BB'. Dans ce cas les conjonctions sont proches des extrémités de l'arc BB' et l'opposition comprise entre ces deux conjonctions est proche du noeud de l'orbite lunaire. De même on peut avoir deux oppositions dans l'arc BB'. Dans ce cas les oppositions sont proches des extrémités de l'arc BB' et la conjonction comprise entre ces deux oppositions se trouve proche du noeud de l'orbite lunaire. De plus comme nous l'avons déjà signalé, les éclipses proches des extrémités de l'arc BB' donc loin du noeud sont des éclipses faibles, donc des éclipses partielles de Soleil ou des éclipses de Lune par la pénombre et les éclipses proches du noeud sont des éclipses fortes, donc des éclipses centrales de Soleil ou des éclipses totales de Lune.
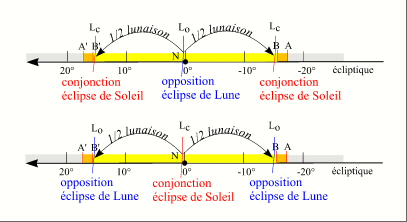
Conjonction et opposition au voisinage du noeud
Crédit : IMCCE/Patrick Rocher
On peut donc avoir une série de trois éclipses, au voisinage du passage de la Terre (ou du soleil apparent) par un noeud de l'orbite lunaire. Dans ce cas, on a soit une éclipse forte de Soleil (éclipse centrale) encadrée par deux éclipses faibles de Lune (éclipses par la pénombre) soit une éclipse forte de Lune (éclipse totale) encadrée par deux éclipses faibles de Soleil (éclipses partielles).
Nombre d'éclipses par an
Une année civile du calendrier grégorien comporte 365 ou 366 jours. La lunaison moyenne est de 29,53 jours, une année lunaire de douze lunaisons a donc 354 jours, l'écart entre les deux années est de 11 ou 12 jours. Durant ces jours, la demi-lunaison étant supérieure à 14 jours, il ne peut pas y avoir à la fois une conjonction et une opposition. Donc une année civile ne peut jamais avoir à la fois 13 conjonctions (nouvelles Lunes) et 13 oppositions (pleines Lunes). Une seule de ces deux conjonctures est possible, dans ce cas la première conjonction ou opposition a lieu dans les 11 (ou 12) premiers jours de janvier et la dernière conjonction ou opposition a lieu dans les 11 (ou 12) derniers jours de décembre. On a donc, au maximum, soit une année civile à 13 oppositions, soit une année civile à 13 conjonctions. La saison des éclipses est égale à 173,31 jours, donc tous les 173 jours, aux conjonctions et oppositions les plus proches de ces dates il y a au moins deux éclipses (une de Soleil et une de Lune) et il y a au plus trois éclipses (deux de Lunes et une de Soleil ou deux de Soleil et une de Lune).
Nombre d'éclipses par an-2
Une année civile peut contenir au maximum deux saisons d'éclipses entières, soit trois passages de la Terre par un des noeuds de l'orbite lunaire, le premier étant en début d'année, le second en milieu d'année et le dernier en fin d'année. À chacun de ces passages, on peut associer un couple ou un triplet d'éclipses. Mais l'on n'a jamais un triplet d'éclipses complet en début et en fin d'année, et dans le cas ou l'on a deux triplets complets à deux passages consécutifs le troisième passage ne comporte qu'une éclipse dans l'année en cours, car s'il présentait deux éclipses dans l'année en cours, il y aurait 13 oppositions et 13 conjonctions dans l'année, chose impossible. Donc dans une année civile, on a au maximum sept éclipses.
Nombre d'éclipses par an-3
Le tableau ci-contre regroupe toutes les combinaisons possibles.
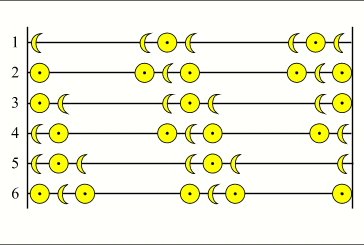
Liste des combinaisons possibles de 7 éclipses dans une année civile
Crédit : IMCCE/Patrick Rocher
On remarque dans ce tableau que les triplets d'éclipses qui se suivent à six lunaisons d'intervalle ont la même composition. En effet, comme on l'a déjà signalé, dans chaque triplet, l'éclipse médiane se produit très près du noeud, or l'éclipse médiane du triplet suivant sera forcément une éclipse du même corps, la conjonction ou l'opposition n'ayant avancé que de 4° environ. De plus lorsque l'on a sept éclipses par an la première et la dernière éclipse sont des éclipses du même corps, la première a toujours lieu dans les 11 (ou 12) premiers jours de janvier et la dernière a toujours lieu dans les 11 (ou 12) derniers jours de décembre.
En conclusion le nombre maximal d'éclipses dans une année civile est de sept éclipses, avec obligatoirement deux éclipses de Soleil et deux éclipses de Lune, pour les trois autres toutes les combinaisons sont possibles. Le nombre minimal d'éclipses dans une année est de quatre, avec obligatoirement deux éclipses de Lune et deux éclipses de Soleil.
Les séries courtes d'éclipses
Nous allons nous intéresser à l'évolution des éclipses au cours du temps. Supposons que nous ayons une éclipse de Soleil à une date donnée comment sera l'éclipse suivante ?
Généralement les éclipses successives de Soleil sont séparées par six lunaisons (liées à une saison d'éclipses), donc il y a alternance de noeud lunaire (noeud ascendant et noeud descendant). Nous avons vu que durant une lunaison la Terre (ou le soleil apparent) progressait en moyenne de 30,67° en longitude par rapport à la ligne des noeuds de l'orbite lunaire, donc au bout de six lunaisons la Terre (ou le Soleil apparent) progresse de 6 x 30,67° = 184,02°, donc si dl1 est la différence de longitude entre la conjonction et le noeud de l'orbite lunaire pour la première éclipse, l'éclipse suivante a lieu au noeud suivant et la différence dl2 entre la conjonction et ce noeud est égale à dl1 - (184,02° - 180°) = dl1- 4,02°. Donc la conjonction se déplace par rapport aux noeuds successifs d'environ 4° dans le sens direct d'une éclipse à la suivante.
Les séries courtes d'éclipses-2
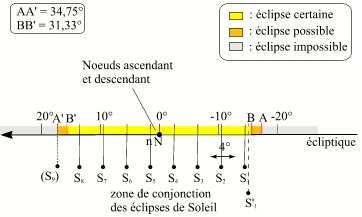
Série courte d'éclipses (vu depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Les éclipses de la suite courte S1 à S8 ont lieu à chaque saison d'éclipse, alternativement au noeud ascendant puis au noeud descendant. Il y a toujours au moins 8 éclipses dans la suite car l'arc BB' contient 7 arcs de 4° donc 8 éclipses. Il peut éventuellement y avoir une neuvième éclipse S9 (dans l'arc A'B'), dans ce cas cette éclipse est la dernière éclipse d'un triplet d'éclipses : Soleil-Lune-Soleil. Dans ce cas la conjonction correspondant à la première éclipse du triplet a lieu une lunaison plus tôt et se trouve 30,67° en amont et cette éclipse est la première éclipse de la série courte suivante; nous avons donc un décrochage dans la suite des séries, la série suivante commence avant que la série en cours ne soit terminée. Ce phénomène peut également se produire lorsque la huitième éclipse de la série est très proche du point B'. On peut donc conclure que les éclipses des suites courtes sont séparées par six lunaisons et que la première éclipse d'une suite courte est séparée de la dernière éclipse de suite courte précédente par cinq lunaisons ou par une lunaison dans le cas d'un décrochage.
Les séries courtes d'éclipses-3
On remarque que les conjonctions liées aux éclipses d'une série courte parcourent l'arc BB' dans le sens direct avec un pas moyen de 4°, les premières et les dernières éclipses sont des éclipses faibles (éclipses partielles ou éclipses centrales de faible magnitude) et les éclipses du milieu de la série, proches des noeuds, sont des éclipses fortes (éclipses centrales). On rappelle que les types des éclipses centrales : annulaire, totale ou mixte ne dépendent pas de la distance entre la conjonction et le noeud mais des diamètres apparents des corps liés aux positions orbitales de la Lune et du Soleil.
Attention, il ne faut jamais oublier que ces calculs sont faits à l'aide des révolutions moyennes de la Lune, la réalité est toujours un peu différente, l'avance de la conjonction n'est donc jamais exactement égale à 4° mais varie autour de cette valeur moyenne.
Répartition des éclipses sur une période de 22 ans
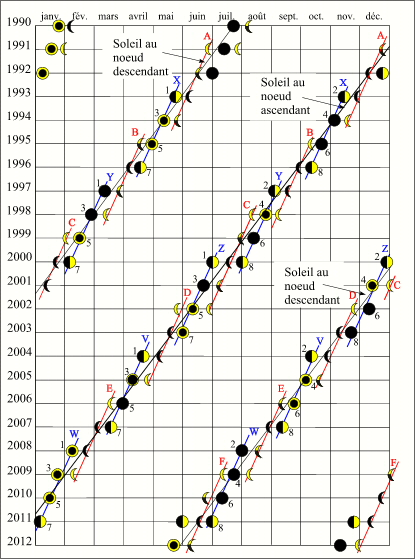
Éclipses de Lune et de Soleil entre 1990 et 2012.
Crédit : IMCCE/Patrick Rocher
Sur le diagramme ci-contre, nous avons fait figurer l'ensemble des éclipses de Lune et de Soleil comprises entre l'an 1990 et l'an 2012. Les éclipses sur ce diagramme sont représentées de la manière suivante :

Crédit : IMCCE/Patrick Rocher
On remarque que les éclipses ont bien lieu aux voisinages des passages du Soleil dans la direction des noeuds ascendant et descendant de l'orbite lunaire. De même on constate qu'à chaque saison d'éclipse on a un doublet d'éclipses Lune-Soleil ou un triplet d'éclipses Lune-Soleil-Lune (1991) ou Soleil-Lune-Soleil (2000) et que dans le cas des triplets les éclipses en première et dernière positions sont faibles et que l'éclipse médiane est forte. On observe que les éclipses de Soleil ou de Lune de début et de fin de séries courtes sont séparées par cinq ou une lunaisons. On vérifie également qu'il y a toujours au moins quatre éclipses par an, sur la période de temps représentée, il n'y a pas d'année à 7 éclipses, mais une année à 6 éclipses (2000).
La démonstration de l'existence des séries courtes de Soleil est également valable pour des séries courtes d'éclipses de Lune. Il suffit de remplacer la conjonction par l'opposition. Sur notre diagramme nous avons fait figurer les séries courtes de Soleil (en bleu) et les séries courtes de Lune (en rouge). On constate que les traits joignant les éclipses d'une même série pour chaque noeud sont parallèles et coupent les lignes des noeuds. Sur la période considérée, il n'y a pas de série courte à 9 éclipses. Mais on peut observer plusieurs décrochage de séries courtes, par exemple la série courte de Soleil Z débute avant que la série Y soit terminée (triplet d'éclipses de l'an 2000).
exercice eclipse soleil
Canons et grandeurs des éclipses de Soleil
Introduction
 Introduction
Introduction
Nous étudions maintenant les éclipses de Soleil sur de très grandes période de temps, pour cela nous construisons des canons d'éclipses.
Les parties pour en savoir plus vous donnent les caractéristiques du canon d'éclipses construit à l'IMCCE, ainsi que les listes des éclipses totales et annulaires les plus longues et des éclipses partielles les plus courtes avec des détails et des commentaires.
Les canons d'éclipses de Soleil
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses de Soleil de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Soleil comprises entre -2003 et 2526.
À l'IMCCE, nous avons construit un canon d'éclipses de Lune et de Soleil. Il porte sur une période de 6000 ans (de l'an -2999 à 3000), il a été construit avec les dernières théories planétaires et lunaire élaborées à l'IMCCE.
Ces trois canons ont été construits avec des théories différentes des corps célestes et avec des constantes légèrement différentes, cela implique que certaines éclipses limites ne sont pas identiques (apparition de nouvelles éclipses limites, ou éclipses totales dans un canon qui deviennent mixtes dans l'autre).
En savoir plus: Le canon de l'IMCCE : les théories utilisées
 En savoir plus
En savoir plus
Pour construire notre canon nous avons utilisé les théories suivantes :
- Théorie de la Lune : ELP2000 de Michèle Chapront-Touzé et J. Chapront.
- Théorie du barycentre Terre-Lune : VSOP82 de P. Bretagnon.
- Éphémérides sous forme de polynômes de Tchebycheff : SLP98 de G. Francou
- TT-TU : valeurs de R. Stephenson (1984) modifiées et adaptées à la théorie de la Lune utilisée.
- Théorie de la précession de Lieske (1977).
- Théorie de la nutation de Wahr (1981).
- Temps sidéral d'Aoki (1992)
En savoir plus: Le canon de l'IMCCE : les paramètres physiques
 En savoir plus
En savoir plus
Les paramètres physiques utilisés sont les suivants :
- le demi-diamètre solaire = 15' 59.63"
- le rapport du rayon lunaire sur le rayon équatorial terrestre : k = 0,2725076
- le rayon équatorial terrestre = 6 378 140 m
- le carré de l'ellipticité de l'ellipsoïde terrestre = 0,00669438 -- 1/f = 1/298.257 IERS (1992)
En savoir plus: Le canon de l'IMCCE : les résultats
 En savoir plus
En savoir plus
Nous avons trouvé sur cette période de 6000 ans, 14 155 éclipses de Soleil qui se répartissent de la manière suivante :
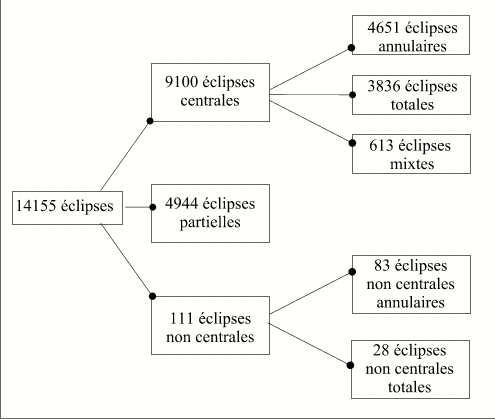
Crédit : IMCCE/Patrick Rocher
Comme on l'a prédit précédemment, on constate qu'il y a bien plus d'éclipses annulaires que d'éclipses totales.
Les éclipses totales les plus longues
Une éclipse totale a une durée maximale lorsque l'ombre est la plus grande possible, c'est-à-dire lorsque la Terre est à l'aphélie pour avoir le plus petit diamètre apparent du Soleil, lorsque la Lune est au périgée pour avoir le plus gros diamètre apparent de la Lune et lorsque le maximum a lieu au zénith du lieu d'observation pour avoir une distance observateur Lune minimale, donc un diamètre de l'ombre maximal. La première condition fixe la date de l'éclipse (actuellement début juillet). La troisième condition fixe le lieu d'observation proche du tropique du Cancer (latitude 23°). Avec la Lune au périgée, la vitesse synodique de l'ombre par rapport à la Terre est de 3 733 km/h (1 037 m/s) et la vitesse de l'ombre sur la surface de la Terre est de 2 196 km/h (610 m/s), le diamètre de l'ombre est alors de 262 km et la durée de l'éclipse est de 7 min 10 s. En réalité, ces paramètres ne sont pas indépendants et l'on s'aperçoit, en faisant un calcul plus rigoureux, que si l'on descend en latitude vers +5° la durée de l'éclipse croît jusqu'à environ 7 min 30 s. En effet le diamètre de l'ombre va décroître (on n'est plus au zénith, l'ombre devient ovale) mais sa vitesse décroît encore plus rapidement ce qui en fin de compte augmente sensiblement la durée de l'éclipse. Le tableau suivant porte sur l'ensemble des éclipses totales comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE.
Les éclipses totales les plus longues-2
| Date |
Durée |
Date |
Durée |
Date |
Durée |
| 29 mai -2584 |
7 min 17,00 s |
10 juin - 2566 |
7 min 23,76 s |
20 juin - 2548 |
7 min 19,94 s |
| 25 avril - 2266 |
7 min 10,49 s |
05 avril - 2248 |
7 min 23,37 s |
16 avril - 2230 |
7 min 27,25 s |
| 27 mai -2212 |
7 min 21,11 s |
8 juin - 1106 |
7 min 10,61 s |
24 mai - 779 |
7 min 13,45 s |
| 05 juin - 761 |
7 min 28,61 s |
15 juin - 743 |
7 min 31,73 s |
26 juin -725 |
7 min 23,45 s |
| 11 mai - 425 |
7 min 16,51 s |
22 mai - 407 |
7 min 18,11 s |
02 juin - 389 |
7 min 10,01 s |
| 22 mai 114 |
7 min 10,41 s |
01 juin 132 |
7 min 19,50 s |
12 juin 150 |
7 min 17,99 s |
| 16 juin 345 |
7 min 21,13 s |
27 juin 363 |
7 min 28,42 s |
08 juillet 381 |
7 min 26,87 s |
| 19 juillet 399 |
7 min 15,75 s |
23 mai 681 |
7 min 14,32 s |
03 juin 699 |
7 min 21,62 s |
| 13 juin 717 |
7 min 20,47 s |
29 mai 1044 |
7 min 16,79 s |
09 juillet 1062 |
7 min 25,27 s |
| 20 juin 1080 |
7 min 22,83 s |
01 juillet 1098 |
7 min 10,21 s |
20 juin 1955 |
7 min 12,62 s |
| 25 juin 2150 |
7 min 18,77 s |
05 juillet 2168 |
7 min 30,89 s |
16 juillet 2186 |
7 min 34,14 s |
| 27 juillet 2204 |
7 min 26,93 s |
08 août 2222 |
7 min 10,39 s |
14 juin 2504 |
7 min 15,03s |
| 25 juin 2522 |
7 min 17,54 s |
23 juin 2867 |
7 min 14,67 s |
03 juillet 2885 |
7 min 15,80 s |
Liste des éclipses totales d'une durée supérieure à 7 minutes et 10 secondes
On constate que l'éclipse la plus longue sera celle du 16 juillet 2186 pour une durée de 7 min 34,14 s, valeur légèrement supérieure à celle calculée avec les valeurs moyennes.
Les éclipses annulaires les plus longues
Dans le cas d'une éclipse annulaire le raisonnement est similaire aux éclipses totales, mais inverse. Le diamètre apparent du Soleil doit être le plus grand possible donc la Terre doit être au périhélie et le diamètre apparent de la Lune doit être le plus petit possible donc la Lune doit être à l'apogée, dans ce cas la durée maximale de l'éclipse peut atteindre 12 min 30 s. Le tableau suivant porte sur l'ensemble des éclipses annulaires comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE .
| Date |
Durée |
Date |
Durée
|
| 12 décembre -1655 |
11 min 53,93 s |
10 décembre - 195 |
11 min 57,93 s |
| 22 décembre - 177 |
12 min 01,43 s |
25 novembre 132 |
12 min 08.01 s |
| 06 décembre 150 |
12 min 15,91 s |
17 décembre 168 |
12 min 07.25 s |
| 25 décembre 1628 |
11 min 55,47 s |
02 décembre 1937 |
11 min 53.63 s |
| 14 décembre 1955 |
12 min 02,49 s |
24 décembre 1973 |
11 min 55.75 s |
Liste des éclipses annulaires d'une durée supérieure à 11 minutes et 50 secondes
Les éclipses partielles les plus petites
À l'aide du canon d'éclipses de Soleil de l'IMCCE nous avons cherché quelles sont les éclipses partielles les plus petites sur la période -2999, 3000. Nous avons trouvé les deux éclipses suivantes :
| Date |
Magnitude |
Instant du maximum |
Durée générale |
| 23 juillet 651 |
0,0008272 |
08h 30 m 41,06 s UT |
9,3 min |
| 17 août 1327 |
0,0004937 |
16 h 58 m 33,03 s UT |
6,2 min |
Nous allons étudier ces deux éclipses.
L'éclipse de 651
Éphémérides de la Lune au voisinage de l'éclipse :
- le 15/07/0651 à 07h 31m 28s UT : Dernier Quartier.
- le 22/07/0651 à 01h 25m 11s UT : la Lune passe par le noeud descendant de son orbite.
- le 22/07/0651 à 14h 50m 11s UT : la Lune à l'apogée, d=406450 km, diam. app. =29,5'.
- le 23/07/0651 à 08h 30m 41s UT : maximum de l'éclipse.
- le 23/07/0651 à 08h 47m 30s UT : Nouvelle Lune.
On constate que cette éclipse a lieu après le passage au noeud descendant de l'orbite lunaire, comme l'éclipse est très faible le passage au noeud doit être loin de la conjonction et l'instant du maximum de l'éclipse loin de l'instant de la conjonction. C'est effectivement le cas, on a un écart de temps égal à 16m 49s entre la conjonction et le maximum de l'éclipse et on a également un écart de temps maximal égal à 31h 22m 19s entre la conjonction et le passage au noeud. Ces valeurs sont presque des valeurs extrêmes car la Lune est voisine de son apogée et la Terre est proche de son aphélie, donc la Lune et le Soleil se déplacent lentement. On remarque que comme nous l'avons expliqué précédemment le maximum de l'éclipse (distance minimale entre le centre de la Lune et le centre du Soleil) a bien lieu entre le passage au noeud et la conjonction.
L'éclipse de 1327
Éphémérides de la Lune au voisinage de l'éclipse :
- le 14/08/1327 à 15h 01m 55s UT : la Lune au périgée d=365783 km, diam. app. =32,7'.
- le 17/08/1327 à 16h 43m 04s UT : Nouvelle Lune.
- le 17/08/1327 à 16h 58m 33s UT : maximum de l'éclipse.
- le 18/08/1327 à 21h 34m 46s UT : la Lune passe par le noeud ascendant de son orbite.
- le 25/08/1327 à 06h 20m 50s UT : Premier Quartier.
- le 26/08/1327 à 12h 15m 12s UT : la Lune à l'apogée d=404381 km, diam. app. =29,6'.
Cette éclipse a lieu avant le passage au noeud ascendant, on a donc le scénario suivant, conjonction, maximum de l'éclipse et passage au noeud. L'écart de temps entre la conjonction et le maximum de l'éclipse est de 15m 29s et l'écart de temps entre la conjonction et le passage au noeud est de 28h 36m 13s.
Pour ces deux éclipses, qui sont des cas extrêmes, on voit que le maximum de l'éclipse est relativement proche de la conjonction, par contre la conjonction est très éloignée du passage au noeud (plus d'une journée).
Les éclipses récentes et futures
Introduction
 Introduction
Introduction
Cette section comporte des cartes représentant les lignes de centralité des éclipses (totales, annulaires et mixtes).
On donne lrs cartes des éclipses centrales sur la période 1998 à 2020, les cartes des éclipses visibles en France depuis le XVIe siècle jusqu'à la fin du XXIe siècle. Des tableaux donnent les zones de visibilité sur le pays.
Les éclipses totale entre 1998 et 2020
La carte ci-contre donne les bandes de totalité des éclipses totales de Soleil entre l'an 1998 et l'an 2020. On remarquera la très grande dispersion des courbes à la surface terrestre. On notera la largeur des bandes de totalité des éclipses proches des pôles et l'étroitesse de la bande de totalité de l'éclipse mixte.
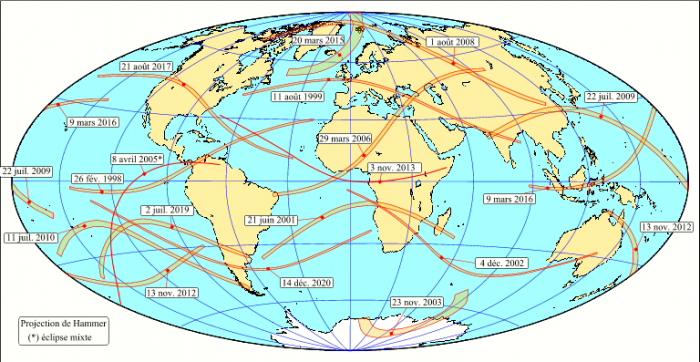
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires entre 1998 et 2020
La carte ci-contre donne les bandes de centralité des éclipses annulaires de Soleil entre l'an 1998 et l'an 2020. On remarquera la très grande dispersion des courbes à la surface terrestre.
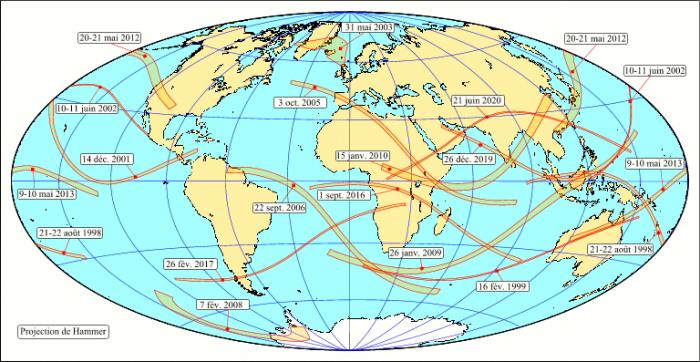
Crédit : IMCCE/Patrick Rocher
Fréquence des éclipses centrales de Soleil en France
Vu la faible surface traversée par la bande de centralité, les éclipses visibles sur un territoire ayant la superficie de la France sont peu nombreuses et si on se limite à une ville où une région, elles deviennent exceptionnelles.
Les tableaux suivants donnent la liste des éclipses dont la bande de centralité traverse la France, il porte sur toutes les éclipses centrales allant du début du XVIe siècle jusqu'à la fin du XXIe siècle.
| Date |
Type d'éclipses |
Remarques |
| 24 janvier 1544 |
totale* |
visible dans le sud-est de la France |
| 12 octobre 1605 |
totale |
visible dans le sud ouest de la France |
| 10 juin 1630 |
totale* |
la fin de l'éclipse est visible de l'ouest au sud-est de la France |
| 27 janvier 1683 |
annulaire |
la fin de l'éclipse est visible à l'ouest et au centre de la France |
| 12 mai 1706 |
totale |
visible dans le sud-est de la France |
| 22 mai 1724 |
totale |
visible du nord-ouest au nord-est de la France , visible à Paris |
| 1 avril 1764 |
annulaire |
visible dans le nord de la France, visible à Paris |
| 7 septembre 1820 |
annulaire |
visible dans le nord-est de la France, invisible à Paris |
| 8 juillet 1842 |
totale |
visible dans le sud-est de la France |
| 9 octobre 1847 |
annulaire |
visible du nord-est au centre-est de la France |
(*) Ces deux éclipses sont données comme mixtes dans le canon de Meeus et comme totales dans le canon d'Oppolzer.
Fréquence des éclipses centrales de Soleil en France-2
| Date |
Type d'éclipse |
Remarques |
| 17 avril 1912 |
mixte |
visible de l'ouest au nord-est de la France, visible au nord de Paris (éclipse perlée) |
| 15 février 1961 |
totale |
visible dans le sud de la France |
| 11 août 1999 |
totale |
visible dans le nord de la France d'ouest en est |
| 5 novembre 2059 |
annulaire |
visible dans le sud-ouest de la France |
| 13 juillet 2075 |
annulaire |
visible en Corse et dans l'extrême sud-est de la France |
| 3 septembre 2081 |
totale |
visible dans le centre de la France |
| 27 février 2082 |
annulaire |
visible dans le sud de la France |
| 23 septembre 2090 |
totale |
fin de l'éclipse visible dans le nord-ouest de la France |
 Remarque
Remarque
Quelques auteurs citent, à tort, l'éclipse du 12 août 2026 comme visible en France. Camille Flammarion la donne visible à Paris (1880, L'Astronomie Populaire). Paul Couderc la dit visible sur une ligne allant de Bordeaux à Toulouse (1971, Les éclipses). En réalité, la phase de totalité de cette éclipse ne sera pas visible en France mais au nord de l'Espagne.
Eclipses du XVI, XVII et XVIIIème siècles, visibles en France
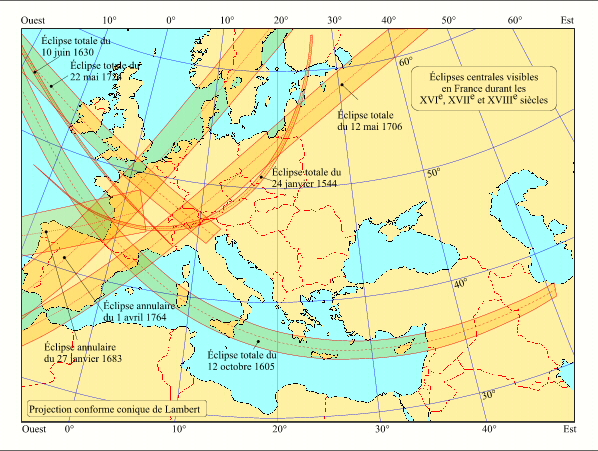
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales, annulaires ou mixtes) visibles en France. On notera la grande diversité de largeur des bandes de centralité.
Eclipses du XIX et du XXème siècles visibles en France
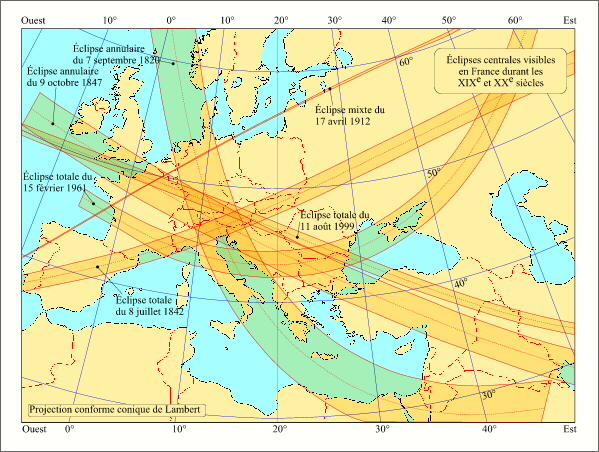
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales, annulaires ou mixtes) visibles en France. L'éclipse de 1912 est une éclipse mixte, elle a été observée au nord de Paris (Saint-Germain en Laye), on notera l'étroitesse de sa ligne de centralité. On notera également que les trajectoires des lignes de centralité présentent des orientations très variées par rapport aux méridiens et aux parallèles terrestres et qu'elles sont loin d'être parallèles à l'équateur terrestre.
Eclipses du XXI siècle visibles en France
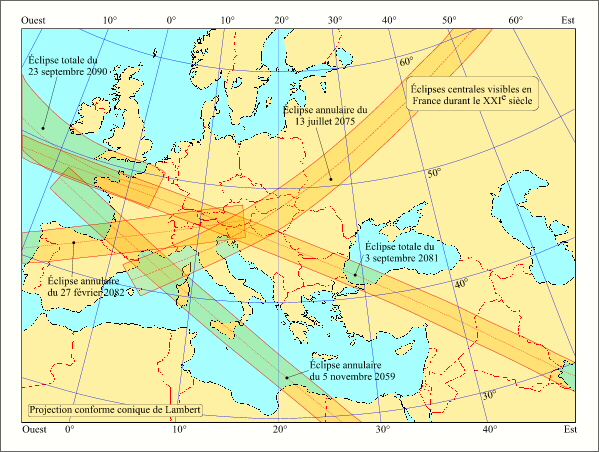
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales et annulaires) visibles sur la France.
Observation d'une éclipse de Soleil
Introduction
 Introduction
Introduction
Cette section est très importante car elle traite des dangers liés à l'observation directe du Soleil. Donc des dangers liés à l'observation d'une phase non totale d'une éclipse.
Précautions à prendre pour observer une éclipse de Soleil
Si on décompose la lumière solaire à l'aide d'un prisme, on aperçoit une série de couleurs allant du violet au rouge. Ces couleurs forment le spectre visible de la lumière solaire. Leurs longueurs d'onde varient de 400 nm (1 nanomètre = 1 millionième de millimètre) pour le violet à 750 nm pour le rouge. Le spectre de la lumière solaire ne se limite pas aux couleurs visibles, mais s'étend dans les basses longueurs d'onde avec les ultraviolets et les rayons X, et vers les grandes longueurs d'onde avec l'infrarouge et les ondes radio. Les rayonnements ultraviolets ont une longueur d'onde comprise entre 15 nm (Rayon X) et 400 nm (lumière visible violet).
On classe le rayonnement ultraviolet en plusieurs catégories :
- les UV C, entre 200 nm et 280 nm, très dangereux, mais ils sont filtrés par l'atmosphère terrestre,
- les UV B, entre 280 nm et 315 nm, qui peuvent engendrer des lésions très graves,
- les UV A, entre 315 nm et 380 nm, qui sont à l'origine du bronzage de la peau et de la photosynthèse de la vitamine D.
Ces rayonnements sont tous nocifs pour la vue, d'où l'usage de lunettes de soleil de bonne qualité pour les journées ensoleillées.
Précautions à prendre pour observer une éclipse de Soleil-2
Les rayonnements infrarouges ont une longueur d'onde comprise entre 800 nm (lumière visible rouge) et 1 mm (ondes radio). Ces rayonnements sont détectés par la chaleur à laquelle ils sont associés.
La concentration du rayonnement solaire permet d'atteindre des températures très élevées. Ainsi, il est très facile d'enflammer une feuille de papier à l'aide d'une loupe et d'un rayon de soleil.
Iriez-vous mettre votre oeil à la place de ce petit bout de papier ? Non ! Alors ne mettez jamais votre oeil derrière un instrument d'optique (lunette, jumelles, appareil photo) qui focalise la lumière solaire et qui n'est pas équipé d'un filtre spécialement conçu pour l'observation solaire.
De même, il est fortement déconseillé de regarder le Soleil à l'oeil nu, même avec des lunettes de soleil. En effet ces lunettes, si elles sont de bonne qualité, protègent du rayonnement ultraviolet mais ne sont nullement conçues pour regarder le Soleil de face car elles n'arrêtent pas le rayonnement infrarouge. On estime, que même lorsque le disque solaire est éclipsé à 99%, le rayonnement solaire peut causer des dommages irréversibles et au moment où vous êtes ébloui il est déjà trop tard.
Précautions à prendre pour observer une éclipse de Soleil-3
Le seul moment, très court, où l'on peut regarder sans danger directement le Soleil durant une éclipse est la phase de totalité.
Mais attention la douleur que l'on ressent en regardant le Soleil en face provient de la pupille qui veut se fermer plus qu'elle ne le peut, c'est cette douleur qui nous fait détourner le regard. Mais un mauvais filtre peut supprimer cette douleur, et laisse passer le rayonnement infrarouge qui va brûler la rétine d'une manière indolore, le fond de l'oeil n'est pas sensible à la douleur et toute brûlure est irréversible.
Il convient donc de prendre énormément de précautions pour observer une éclipse de Soleil.
Une méthode classique consiste à observer le phénomène par projection. Pour cela munissez-vous de deux feuilles de papier cartonné. La première, percée d'un minuscule trou, est positionnée perpendiculairement à la direction du soleil, la deuxième est placée parallèlement à la première ; lorsque cette seconde feuille est suffisamment éloignée de la première (environ un demi-mètre), on peut y observer l'image du soleil. On peut également observer l'éclipse par projection avec un instrument d'optique, par exemple une petite lunette. Pour cela, il suffit d'orienter la lunette vers le Soleil, sans utiliser le chercheur de l'instrument, mais en orientant la lunette de manière à minimiser la dimension de son ombre. La première méthode est absolument sans danger, la deuxième présente le risque de voir une personne distraite ou non informée (souvent des enfants), mettre son oeil derrière l'instrument.
L'utilisation de filtres pour l'observation des éclipses
Les filtres solaires
Il existe de nombreux types de filtres solaires, utilisés par les astronomes professionnels et amateurs pour l'observation du Soleil. Ces filtres ont deux objectifs, réduire l'intensité lumineuse et filtrer les rayonnements ultraviolets et infrarouges. Ces filtres possèdent une fine couche d'aluminium, de chrome ou d'argent sur leur surface. C'est cette couche métallique qui filtre le rayonnement infrarouge. Ces filtres, pour être efficaces, doivent être montés devant les systèmes optiques (devant la lunette où le télescope), cela explique à la fois leur grand diamètre et leur prix souvent élevé. On trouve parfois, vendus avec des lunettes astronomiques du commerce, des filtres solaires qui se placent sur l'oculaire ; ces filtres sont dangereux, en effet, la lumière solaire traverse alors tout le système optique, ce qui concentre le rayonnement ultraviolet et peut briser le filtre par échauffement. On peut utiliser un filtre solaire vissé sur l'oculaire, uniquement s'il est associé avec un hélioscope d'Herschel. Si vous possédez un instrument d'observation consultez votre revendeur qui pourra vous conseiller pour l'achat d'un filtre solaire adapté à votre instrument.
L'utilisation de filtres pour l'observation des éclipses-2
Si vous ne voulez pas investir trop d'argent dans l'achat d'un filtre solaire, vous pouvez confectionner un filtre en Mylar.
Le Mylar se présente sous la forme d'une mince feuille métallique aluminée. Son pouvoir filtrant est très performant, il filtre parfaitement les rayonnements infrarouge et UV et diminue l'intensité lumineuse d'un facteur 1 000 000. Son seul défaut est sa fragilité, due à sa faible épaisseur. Il faut également se méfier d'un éventuel défaut de surface. Utilisez toujours des feuilles parfaitement planes (n'ayant subi aucun pli). Ces feuilles sont faciles à découper et peuvent donc être utilisées pour la création du filtre de votre choix. Vous pouvez en équiper une paire de lunettes. Ainsi, La revue Ciel et Espace en association avec l'ASNAV (Association Nationale pour l'Amélioration de la Vue) a distribué une paire de lunette munie de filtre en Mylar dans son numéro d'octobre 1996, pour l'observation de l'éclipse du 12 octobre 1996. De telles lunettes permettent d'observer les éclipses à " l'oeil nu ", mais, elles ne doivent pas être utilisées pour regarder à travers un instrument. De plus elles ne doivent pas être utilisées après leur date limite d'utilisation.
Le filtre, quel qu'il soit, doit toujours être placé devant l'instrument et non entre l'instrument et l'observateur.
L'utilisation de filtres pour l'observation des éclipses-3
Liste des filtres pouvant être utilisés pour observer une éclipse de Soleil
- filtres solaires spéciaux.
- filtres en Mylar.
- plaques de verre d'indice maximal pour les masques de soudeur.
- plusieurs épaisseurs de négatifs noir et blanc totalement opaques, complètement développés et contenant une émulsion argentine (attention les films négatifs couleurs et certains films négatifs noir et blanc n'en contiennent pas).
Nous vous conseillons vivement les deux premiers, les autres, tenant plus du bricolage, ne sont pas sans risques.
En cas de doute n'hésitez pas à consulter une personne compétente, c'est-à-dire un ophtalmologiste, ou observez l'éclipse par projection.
L'utilisation de filtres pour l'observation des éclipses-4
Liste non exhaustive des filtres À NE PAS utiliser
- Les morceaux de verre noirci à la flamme d'une bougie.
- Les filtres photographiques en gélatine.
- Les filtres polarisants, croisés ou non.
- Les plaques rayons X exposées.
- Les négatifs couleurs ou les négatifs noir et blanc ne contenant pas d'émulsion argentine.
- Une ou plusieurs paires de lunettes.
Les traumatismes causés par le Soleil
Si vous regardez sans précaution une éclipse de Soleil, vous risquez une brûlure grave du fond de l'oeil. Au moment de la brûlure, ce traumatisme est le plus souvent indolore (d'où son danger). Il peut entraîner des cécités définitives ou partielles. Lors de la dernière éclipse visible aux États-Unis, on a dénombré plus de 1 000 cas de cécité définitive et plus de 10 000 cas de cécité temporaire. Même dans les cas de cécité temporaire le traumatise est très long à se résorber (cela peut prendre de 6 mois à un an) et il reste toujours des séquelles. Contrairement à ce que l'on pourrait penser le fait de porter des lunettes de Soleil augmente l'intensité de la brûlure, en effet l'intensité lumineuse étant filtrée par les lunettes, la pupille de l'oeil se dilate et la quantité de lumière infrarouge qui pénètre dans l'oeil est plus importante, d'où une brûlure encore plus intense.
Récurrences des éclipses de Soleil
Auteur: P. Rocher - IMCCE - Observatoire de Paris
Introduction
 Introduction
Introduction
Ce chapitre est le plus complexe des chapitres sur les éclipses. Dans ce chapitre nous étudions les périodes de récurrence des éclipses de Soleil. Nous voyons qu'il existe plusieurs périodes de récurrence, notamment le Saros. Nous expliquons pourquoi cette période est réellement une bonne période de récurrence en analysant les principales perturbations lunaires et en introduisant la notion de révolution anomalistique. Nous définissons ensuite les suites d'éclipses séparées par cette période de temps. Ce sont des séries longues de Saros. Nous commentons et expliquons leur évolution : évolution des types d'éclipses, évolution des magnitudes, évolution des zones de visibilité sur Terre.
Enfin nous étudions les éclipses anciennes et leur utilisation pour déterminer le ralentissement de la révolution terrestre.
 Prérequis
Prérequis
Les périodes de récurrences des éclipses
Introduction
 Introduction
Introduction
Cette partie est le plus complexe des chapitres sur les éclipses. Dans cette partie du cours nous étudions les périodes de récurrence des éclipses de Soleil. Nous voyons qu'il existe plusieurs périodes de récurrence, notamment le Saros. Nous expliquons pourquoi cette période est réellement une bonne période de récurrence en analysant les principales perturbations lunaires et en introduisant la notion de révolution anomalistique. Nous définissons ensuite les suites d'éclipses séparées par cette période de temps. Ce sont des séries longues de Saros. Nous commentons et expliquons leur évolution : évolution des types d'éclipses, évolution des magnitudes, évolution des zones de visibilité sur Terre.
Enfin nous étudions les éclipses anciennes et leur utilisation pour déterminer le ralentissement de la révolution terrestre.
Dans cette première section, nous définissons les périodes de révolutions qui permettent de trouver les périodes de récurrence des éclipses de Soleil. Nous introduisons la notion de Saros. La partie "pour en savoir plus" décrit la méthode de décomposition d'un réel en fractions continues et comment l'on retrouve la période du Saros, elle donne également d'autres périodes de récurrence connues sous le nom de Saros chinois. Nous donnons ensuite l'origine du terme erroné de Saros et les caractéristiques des éclipses contenues dans une séries de Saros.
Les périodes de récurrence
Nous avons vu que les éclipses de Soleil et de Lune se produisent lorsque les syzygies (la conjonction et l'opposition de la Lune) ont lieu avec le soleil apparent au voisinage de la direction de la ligne des nœuds de l'orbite lunaire. Le retour d'une même phase lunaire est lié à la révolution synodique « L » (29,5305888532 jours) de la Lune. Le retour du Soleil dans la direction de la ligne des nœuds au moment des syzygies est équivalent au retour de la Lune près de ses nœuds, ce retour est lié à la révolution draconitique « G » (27,212220817 jours) de la Lune. Une période de récurrence des éclipses doit donc être un multiple commun à ces deux périodes.
On doit donc déterminer deux nombres x et y tel que x.G=y.L ou encore tel que x/y=L/G.
Les valeurs possibles pour x et y se calculent en utilisant la méthode de décomposition des réels en fractions continues.
Périodes de récurrence-2
Le rapport L/G est égal à 1,085195841, il s'écrit sous forme réduite : (1;11,1,2,1,4,3,5,1).
Ce qui donne pour x et y les solutions suivantes :
| x |
1 |
12 |
13 |
38 |
51 |
242 |
777 |
4127 |
| y |
1 |
11 |
12 |
35 |
47 |
223 |
716 |
3803 |
Le cycle correspondant à la solution 242/223, soit 223 lunaisons, est connu à tort sous le nom de saros. 223 lunaisons sont égales à 6585,321314 jours et 242 révolutions draconitiques sont égales à 6585,357436 jours, la différence 242L - 223L est de 0,03612 jour, soit 52 minutes.
On exprime parfois cette période en années et en jours, mais cela n'est pas recommandé, car 6 585 jours donnent 18 ans, plus 10 ou 11 ou 12 jours, cela dépend du nombre d'années bissextiles comprises dans les 18 années (5,4 ou 3), il est préférable de garder cette expression en jours.
Périodes de récurrence-3
Pourquoi le saros est une période de récurrence ?
La principale inégalité dans la longitude de la Lune, l'équation du centre, est fonction de sa distance angulaire au périgée de son orbite, cette distance angulaire porte le nom d'anomalie. L'intervalle de temps qui sépare en moyenne le passage de la Lune par la direction de son périgée, s'appelle la révolution anomalistique. Sa valeur moyenne est A = 27,554549878 jours. Il est très important de constater que le saros est également un multiple de cette révolution anomalistique, ainsi après un saros, non seulement on retrouve la même configuration Soleil Terre Lune mais la plus grosse inégalité dans la longitude de la Lune a presque la même valeur, donc on retrouve pratiquement le même écart entre la Lune vraie et la Lune moyenne. C'est principalement pour cette raison que le saros est une période de récurrence des éclipses. En effet le saros est construit à partir des révolutions synodique et draconitique moyennes de la Lune. Or l'écart entre la révolution synodique vraie et la révolution synodique moyenne de la Lune peut atteindre plus ou moins sept heures, or en sept heures la position de la Lune varie en moyenne de 3,5° en longitude (si l'on tient compte des perturbations cet écart peut atteindre 7,5°). Or comme les diamètres apparents de la Lune et du Soleil sont de l'ordre du demi-degré, il est totalement impossible de prédire une éclipse du Soleil uniquement avec la connaissance de la révolution synodique moyenne, seule la connaissance de la lunaison vraie permet cette prédiction. Donc si une période de récurrence utilise les révolutions synodique et draconitique moyennes, il faut également que cette période ramène la Lune vraie au même endroit par rapport à la Lune moyenne, donc que la période de récurrence soit aussi un multiple de la période de la plus grosse inégalité dans la longitude de la Lune.
On a 239 A = 6585,537419 jours et 1 saros = 239 A - 0,0079 A, au bout d'un saros, la Lune se retrouve donc à 2,8° en amont sur sa position orbitale.
Périodes de récurrence-4
Le saros ramène également le Soleil près des noeuds, il doit donc être aussi un multiple de l'année des éclipses E (346,62 jours) et l'on a bien 19 E = 6585,78 jours, l'écart avec le saros n'est que de 0,46 jour. Cette condition, moins stricte que le retour de la Lune à son noeud entraîne une légère évolution des éclipses d'un saros à l'autre.
Les inégalités dans le mouvement du soleil apparent sont également fonction de sa position angulaire par rapport à son périgée (périhélie de la Terre), cet angle porte le nom d'anomalie. La période de révolution qui ramène le soleil apparent à son périgée (ou la Terre à son périhélie), s'appelle révolution anomalistique ou année anomalistique et elle est égale à : a = 365,2596 jours.
Or 18 a = 6574,67 jours, l'écart avec le saros est de 10,65 jours, donc au bout d'un saros le soleil apparent ne s'est déplacé que de 10° sur son orbite par rapport à sa position un saros plus tôt, ce qui correspond à un décalage de 10° vers l'est parmi les constellations zodiacales.
En savoir plus: Décomposition d'un réel en fractions continues
 En savoir plus
En savoir plus
La décomposition d'un réel en fractions continues a été créée par Laplace en 1768, son but était d'obtenir une approximation d'un réel positif r sous la forme d'un quotient de deux entiers. La méthode consiste à décomposer le réel en partie entière et en partie décimale : r = a0 + u1, u1 étant inférieur à 1, on prend son inverse et on continue comme précédemment en itérant avec les restes successifs :
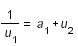
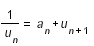
En remplaçant les ui par leurs expressions, le réel se présente sous la forme de fractions emboîtées qui forme la fraction continue :
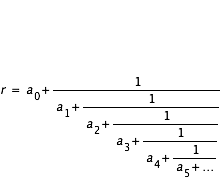
En savoir plus: Décomposition d'un réel en fractions continues-2
 En savoir plus
En savoir plus
On obtient des approximations successives de r au moyen de rapports d'entiers en tronquant le développement de la fraction à des ordres plus ou moins élevés que l'on appelle les réduites d'ordre n :
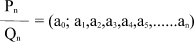
On passe de l'ordre n et n-1 à l'ordre n+1 par la relation de récurrence du second ordre suivante :
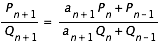
Ces formules de récurrence permettant ce calcul furent découvertes par le mathématicien Indien Bhascara II au début du XIIIe siècle, soit 5 siècles avant que le mathématicien Anglais John Wallis ne les redécouvre en Europe.
 Exemple
Exemple
représentation du nombre 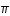
On a 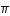 = 3,141592654
= 3,141592654
Sa forme réduite d'ordre 4 s'écrit : (3;7,15,1,293)
Les approximations successives sont : 3, 22/7, 333/106, 355/113, 104348/33215.
En savoir plus: Autres périodes de récurrence
 En savoir plus
En savoir plus
Comme nous venons de le voir, pour qu'une période soit une période de récurrence des éclipses, il faut non seulement qu'elle soit un multiple des révolutions synodique (L) et draconitique (G) de la Lune, mais il faut également qu'elle soit un multiple de la révolution anomalistique (A) de la Lune. On doit donc trouver trois nombres x, y et z tels que x.L ~ y.G ~ z.A. Le tableau suivant donne une série de solutions.
| jours |
x |
y |
z |
Durée (ans) |
| |
223 |
242 |
239 |
18,03 |
| 6585+ |
0,321 |
0,357 |
0,537 |
|
| |
2148 |
2331 |
2302 |
173,7 |
| 63430+ |
1,705 |
1,684 |
0,574 |
|
| |
2371 |
2573 |
2541 |
191,7 |
| 70016+ |
1,026 |
1,042 |
0,112 |
|
La première ligne correspond au saros, les deux solutions suivantes ramènent bien la lunaison et la Lune près de son noeud, mais décalent beaucoup plus la Lune par rapport à son périgée (14,8° pour la seconde et 11,9° pour la troisième). Elles sont donc moins stables que le saros.
En savoir plus: Autres périodes de récurrence-2
 En savoir plus
En savoir plus
On peut également chercher des solutions sous la forme x.L ~ 2.y.G/2 ~ z.A. Ces solutions font intervenir la demi-révolution draconitique, cela correspond donc à des récurrences avec alternance de noeud. Le tableau suivant donne une série de solutions.
| jours |
x |
y |
z |
Durée (ans) |
| |
135 |
146,5 |
145 |
10,92 |
| 3986+ |
0,629 |
0,590 |
9,41 |
|
| |
1074 |
1165,5 |
1151 |
86,83 |
| 31715+ |
0,852 |
0,842 |
0,287 |
|
| |
1297 |
1407,5 |
1390 |
104,86 |
| 38300+ |
1,174 |
1,199 |
0,824 |
|
La première solution que l'on appelle «saros chinois» car elle était connue des chinois, n'est pas très stable à cause de l'écart en anomalie. La seconde et la dernière solution sont meilleures car les écarts en anomalie sont beaucoup plus faibles.
Ainsi pour la seconde solution : 1074.L - 1165,5.G = 0,009 jour = 13 minutes et 1074.L - 1151.A = 0,56 jour, au bout d'un cycle, la Lune se retrouve à 7,4° en aval sur sa position orbitale.
Et pour la dernière solution : 1297.L - 1407,5.G = -0,027 jour = -39 minutes et 1297.L - 1390.A = 0,35 jour, au bout d'un cycle, la Lune se retrouve à 4,5° en aval sur sa position orbitale.
L'origine du nom "saros"
Edmont Halley (1656 - 1742) publia en 1961 dans les Philosophical Transactions un mémoire dans lequel il proposait de corriger un passage de l'Histoire naturelle de Pline l'Ancien (23 - 79 ap. J.-C.) où il était question de la période de récurrence des éclipses (Histoire Naturelle, II, 56). Le texte est le suivant : " Il est sûr que les éclipses se reproduisent dans le même ordre au bout de 222 mois ". Sur d'autres manuscrits on trouve les valeurs de 213 et 293 mois. Halley corrige à juste titre la valeur de 222 mois en 223 mois.
En consultant une encyclopédie byzantine du Xe siècle, la Souda, il trouva la mention du mot saros dans le texte suivant " Saros, mesure et nombre chez les Chaldéens. Un saros contient 222 mois lunaires qui font 18 ans et 6 mois. 120 saros correspondent à 2222 années ". Croyant à tort que la Souda dépendait ici de Pline, Halley en conclut que les Chaldéens appelaient saros la période de 223 ans de Pline.
Le terme sar en sumérien a le sens d'univers, et en temps que nombre, il représente la quantité 3600. Dans le sens de 3 600 ans le terme saros est utilisé par Berossos (~290 avant J.-C.) et après lui par Abydenus (deux siècles avant J.-C.) puis par Synkellos en l'an 800 après J.-C.
L'origine du nom "saros"-2
La Souda nomme saros une période de 222 mois lunaires et dit explicitement qu'elle correspond à 18 ans et 6 mois avec une année de 12 mois lunaires. La période portant le nom de saros chez les Chaldéens n'a donc rien à voir avec les éclipses.
L'erreur de Halley a été dénoncée par l'astronome Guillaume Le Gentil de La Galaisière (1725 - 1792) dans deux articles très critiques publiés en 1756, alors que Montucla refait l'erreur d'Halley dans son Histoire des mathématiques (1758). D'autres astronomes et historiens essaieront en vain de corriger l'erreur d'Halley : Ideler en 1825, Tannery en 1893, Schiaparelli en 1908, Bigourdan en 1911 et Pannekoek en 1917.
Cette erreur sera amplifiée par la légende de Thalès de Milet (VIe siècle avant J.-C.) rapportait par Hérodote (484 à 425 avant J.-C.) dans l'Enquête (p. 174) Thalès avait prédit aux Ioniens un obscurcissement du Soleil " pour l'année dans laquelle elle se produisit ". Cette éclipse aurait permis de mettre fin à une guerre entre les Mèdes et les Lydiens.
Nombre d'éclipses dans un saros
Le saros comporte 38 saisons d'éclipses, revenant en moyenne toutes les 5 ou 6 lunaisons. À chaque saison d'éclipses il y a au moins deux éclipses et parfois trois éclipses. En moyenne un saros comprend 84 éclipses, réparties en 42 éclipses de Soleil et 42 éclipses de Lune.
Les 42 éclipses de Lune se répartissent de la manière suivante : 14 éclipses par la pénombre, 28 éclipses par l'ombre dont 14 éclipses partielles et 14 éclipses totales.
Les 42 éclipses de Soleil se répartissent de la manière suivante : 14 éclipses partielles et 28 éclipses centrales.
Ce nombre d'éclipses par saros est une valeur moyenne, en réalité il existe des saros riches pouvant atteindre jusqu'à 94 éclipses (47 de chaque) et des saros pauvres comportant 78 éclipses.
Les canons d'éclipses construits à l'IMCCE comportent 28512 éclipses sur une période de 5999 ans, soit en moyenne 4,7528 éclipses par an et 85,7 éclipses par saros (valeur que l'on peut arrondir à 86). Cette valeur est légèrement plus forte que la valeur moyenne (84). On retrouve le saros moyen du canon d'Oppolzer, construit sur une période plus courte, qui est de 86 éclipses.
Les suites longues d'éclipses
Introduction
 Introduction
Introduction
Dans cette section nous définissons la notion de suite longues d'éclipses de Soleil liée au Saros. Nous regardons comment évoluent les éclipses qui se succèdent dans ces suites. Nous traitons dans la partie pour en savoir plus, l'évolution géographique des éclipses des suites longues à la surface du globe terrestre et nous donnons les limites de prédiction locale à partir de la connaissance du Saros. En fin de section nous donnons et commentons un exemple de série longue.
Eclipses homologues et suites longues
Nous avons vu qu'il existe une période de récurrence des éclipses, le saros, qui ramène sensiblement la même éclipse après une période de 6585,32 jours. Ces éclipses séparées par un saros sont appelées éclipses homologues. En réalité, elles ne sont pas parfaitement identiques, mais elles évoluent légèrement d'un saros à l'autre et elles forment des suites qui portent sur de grandes périodes de temps d'où leur nom de suites longues.
Eclipses homologues et suites longues-2
Evolution de la longitude de la conjonction après un saros
Nous allons regarder comment évolue la longitude de la conjonction après une période d'un saros. L'écart entre le saros de 223 lunaisons « L » et les 242 révolutions draconitiques « G » est de moins 52 minutes de temps (- 0,03612 jour).
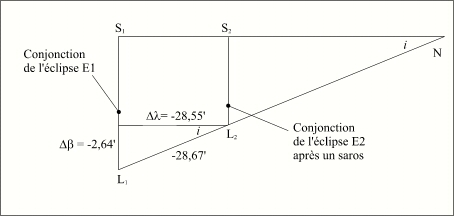
Crédit : IMCCE/Patrick Rocher
Durant ces 52 minutes la Lune, sur son orbite, se déplace en moyenne par rapport à son noeud de -0,03612 x 360°/G = -28,67'. La Lune en conjonction se trouve donc déplacée sur son orbite de 28,67' dans le sens rétrograde par rapport au noeud. Compte tenu de l'inclinaison de l'orbite lunaire, ce décalage se traduit par un décalage de la longitude céleste Δ
λ = -28,55' et par une variation de la latitude céleste de la Lune de Δ
β = -2,64'.
Eclipses homologues et suites longues-3
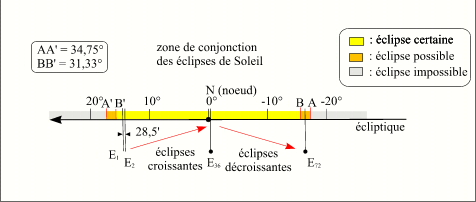
Crédit : IMCCE/Patrick Rocher
Les conjonctions des éclipses homologues vont donc parcourir l'arc BB' dans le sens rétrograde avec un pas moyen de 28,55'. Si l'on divise l'arc BB' par 28,55', on constate qu'il peut contenir 66 éclipses et si l'on divise l'arc AA' par 28,55' on voit qu'il peut contenir 74 éclipses. Ces séries d'éclipses sont appelées suites longues. L'étude des canons d'éclipses montre qu'en moyenne ces suites comportent 72 éclipses. Ce qui correspond à une période de temps d'environ 1300 ans.
Eclipses homologues et suites longues-4
Aspects des éclipses d'une suite longue
Les premières éclipses d'une suite longue sont faibles, car elles sont proches de l'arc A'B', donc loin du noeud. Ensuite, leur grandeur va croître jusqu'à ce qu'elles se produisent au voisinage du noeud, puis leur grandeur va décroître pour finir de nouveau faible au voisinage de l'arc BA. Pour une suite longue de 72 éclipses, si l'on respecte les pourcentages des éclipses partielles et des éclipses centrales (1/3 et 2/3), on aura donc successivement 12 éclipses partielles de grandeur croissante (sur 200 ans), puis 24 éclipses centrales de grandeur croissante (sur 450 ans), puis 24 éclipses centrales de grandeur décroissante (sur 240 ans) et enfin 12 éclipses partielles de grandeur décroissante (sur 200 ans). Dans la pratique, les deux ou trois éclipses du milieu de la suite longue sont maximales, elles servent de transition entre la période de croissance et de décroissance des éclipses. On remarque que toutes les éclipses d'une suite ont lieu au même noeud. Si la suite longue a lieu au noeud descendant les latitudes célestes successives de la Lune croissent des latitudes négatives aux latitudes positives, l'ombre et la pénombre vont donc se déplacer sur la Terre du sud au nord. Inversement pour une suite longue au noeud ascendant les latitudes célestes successives de la Lune décroissent des latitudes positives aux latitudes négatives, l'ombre et la pénombre vont donc se déplacer sur la Terre du nord au sud.
Evolutions des éclipses homologues
Evolution en longitude terrestre
Nous avons vu que la période du saros n'est pas un nombre entier de jours, sa valeur est de 6585,32 jours. Donc entre deux éclipses homologues, la Terre n'a pas tourné d'un nombre entier de jour, les zones concernées par les éclipses ne sont donc pas les mêmes. En 0,32 jour la Terre tourne d'environ 120°, les zones concernées par l'éclipse se déplacent donc d'environ 120° vers l'ouest. Ce décalage est bien visible sur la carte ci-contre, où nous avons tracé les lignes de centralité des éclipses homologues à l'éclipse du 11 août 1999.
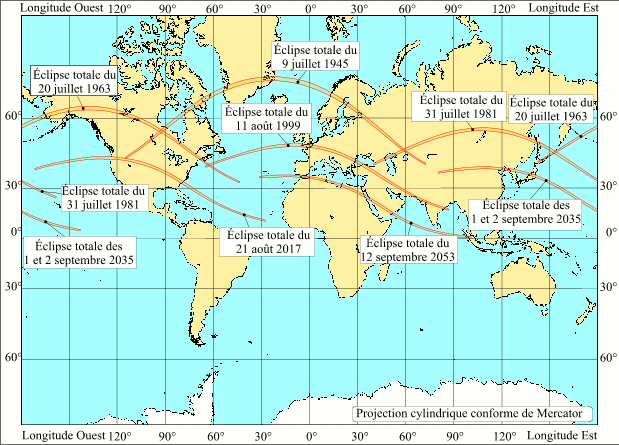
Sept éclipses homologues de la suite longue contenant l'éclipse du 11 août 1999
Crédit : IMCCE/Patrick Rocher
Evolutions des éclipses homologues
Evolution en latitude terrestre
Nous avons vu que les suites longues au noeud ascendant parcourent la Terre du nord au sud et que les suites longues au noeud descendant parcourent la Terre du sud au nord. Le décalage en latitude terrestre provient du décalage en latitude céleste de la Lune d'une éclipse homologue à l'autre. Un décalage en latitude céleste Δβ de la Lune, même si le sens du décalage est conservé, ne se traduit pas directement par un même décalage de l'ombre en latitude terrestre. En effet, les latitudes célestes sont comptées à partir de l'écliptique et les latitudes terrestres sont comptées à partir de l'équateur terrestre, on doit donc tenir compte de l'obliquité de l'écliptique sur l'équateur terrestre, ainsi les variations de latitude céleste sont inclinées d'environ 23° par rapport au méridien terrestre. De plus la variation de latitude doit être projetée sur une sphère et la projection sur la sphère terrestre produit un décalage plus important près des pôles. Sur la figure ci-contre, Δβ représente la variation de latitude céleste de la Lune, à cette variation correspond une variation Δr sur l'axe normal à l'écliptique (pôle de l'écliptique) et une variation Δl sur la sphère terrestre, cette variation a deux composantes, une composante Δλ en longitude terrestre, qui produit le léger décalage en longitude vers l'est, et une composante en latitude terrestre Δϕ.
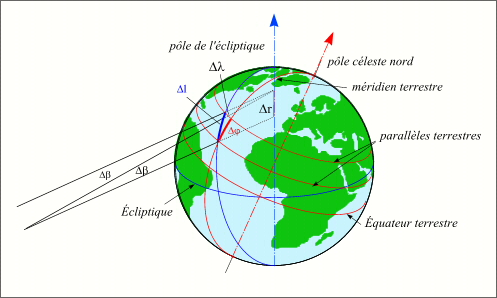
Variation de la latitude terrestre
Crédit : IMCCE/Patrick Rocher
Cela explique qu'après une période de trois saros (ou Exeligmos) les lignes de centralité ne sont pas alignées en longitude, comme on pourrait si attendre après trois décalages de 120° en longitude, mais sont décalées légèrement vers l'est comme on le constate sur la carte des éclipses homologues à l'éclipse du 11 août 1999.
En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues
 En savoir plus
En savoir plus
Nous allons essayer de quantifier un peu mieux les décalages en latitude. En moyenne, au bout de trois saros les lignes de centralité des éclipses se décalent d'environ 900 km dans le plan passant par la Terre et normal à l'axe des cônes (plan de Bessel), elles parcourent donc la Terre en environ 45 saros. On retrouve approximativement le nombre d'éclipses centrales dans une suite longue (48).
Mais il convient de noter que la variation en latitude des séries homologues ne se fait pas toujours de façon uniforme d'un pôle à l'autre. Elle peut être momentanément inversée ou accélérée. Prenons le cas d'une suite longue au noeud ascendant, les lignes de centralité parcourent la sphère terrestre du nord au sud. Après trois saros la ligne de centralité descend d'environ 900km ce qui correspond à une variation de la latitude de la Lune de 7,92' (3 x 2,64'). Or dans ce mouvement nous n'avons considéré que le déplacement en latitude de la Lune, le Soleil étant toujours dans l'écliptique.
En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues-2
 En savoir plus
En savoir plus
En réalité comme l'écliptique est incliné de 23° par rapport à l'équateur terrestre, nous devons également tenir compte des variations des hauteurs du Soleil par rapport à l'équateur terrestre, donc des variations de déclinaison du Soleil, or ces variations peuvent être très grandes par rapport aux variations en latitude de la Lune. Ainsi trois saros font environ 54 ans et 34 jours, donc au bout de trois saros le Soleil se retrouve décalé d'environ 34° sur l'écliptique, cette variation de 34° sur l'écliptique, si elle est répartie de part et d'autre d'un équinoxe peut se traduire par des variations en déclinaison de plus au moins 13°, ce qui correspond à une variation de hauteur de 13° du Soleil dans le méridien, à midi, c'est-à-dire une descente (si on est de part et d'autre de l'équinoxe de d'automne) ou une remontée (si on est de part et d'autre de l'équinoxe printemps) de 1440 km environ. Une descente du Soleil en déclinaison fait remonter l'ombre donc la ligne de centralité et une montée du Soleil fait redescendre l'ombre donc la ligne de centralité. Ainsi dans une série longue, lorsque les dates des séries homologues séparées par trois saros se trouvent distribuées autour des équinoxes, les latitudes de la bande de centralité peuvent être accentuées de 1440 km (1440+900 = 2340 km) ou diminuées de 1440km (900-1440 = -540 km). Ce phénomène est localisé dans le temps et disparaît lorsqu'on s'éloigne des dates des équinoxes.
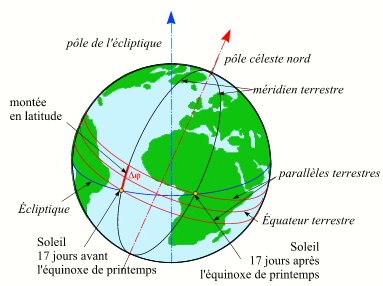
Variation de la hauteur du Soleil au méridien de part et d'autre des équinoxes
Crédit : IMCCE/Patrick Rocher
Evolutions des éclipses homologues - suite
Variation sur le fond d'étoile et dans l'année
Nous rappelons que d'un saros à l'autre, le Soleil, donc l'éclipse se décale d'environ 10,5° par rapport aux constellations zodiacales. Au cours d'une suite longue le soleil apparent effectue plus de deux tours complets d'orbite et l'on rencontre toutes les configurations liées au soleil apparent. Les éclipses parcourent les quatre saisons et cela deux fois.
Variation des types d'éclipses
Nous avons vu également que suite à l'écart entre un saros et 239 révolutions anomalistiques, la distance de la Lune à son périgée varie de 2,8° d'un saros à l'autre. Au cours d'une suite longue de 72 saros, les conjonctions lunaires liées aux éclipses homologues (donc la Lune) ne vont parcourir que 202° de l'orbite lunaire, soit un peu plus que la moitié. De plus durant les 48 éclipses centrales du saros, cet arc se réduit à 134°, il convient de comparer cette valeur avec les portions de l'orbite lunaire où les éclipses sont totales ou annulaires.
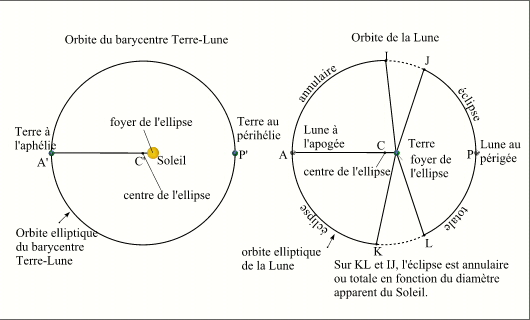
Orbites de la Terre et de la Lune
Crédit : IMCCE/Patrick Rocher
Ainsi si le périgée est proche du milieu de cet arc de 134°, la suite longue est trés riche en éclipses totales, si au contraire, cet arc avoisine l'apogée la suite longue est trés riche en éclipses annulaires.
Evolutions des éclipses homologues - suite2
Remarques supplémentaires
Il ne faut jamais perdre de vue que toutes les variations dans les suites longues sont calculées avec des valeurs moyennes et ne sont jamais toute à fait conformes avec la réalité. Ainsi le décalage de la conjonction par rapport au noeud de 28,55' est une valeur moyenne. En réalité, le Soleil avance plus vite en janvier (il est proche du périgée) qu'en juillet (proche de l'apogée), le calcul montre que la variation de la longitude de la conjonction par rapport au noeud est de l'ordre de 6' en janvier (au lieu de 28,55') et qu'elle atteint 48' en juillet. Les éclipses homologues d'hiver sont donc plus semblables que les éclipses homologues d'été qui évoluent sensiblement plus vite.
Il est facile de connaître la position d'une éclipse dans une suite longue d'éclipses. Les éclipses croissantes ont toujours lieu après le passage au noeud et les éclipses décroissantes ont toujours lieu avant le passage au noeud. La connaissance des instants des syzygies et du passage au noeud permet donc de positionner l'éclipse dans sa suite longue. Inversement la connaissance de la position d'une éclipse dans sa suite longue permet, sauf pour l'éclipse maximale, de savoir sa position par rapport aux noeuds. De plus dans le cas d'un doublet d'éclipses (Lune Soleil ou Soleil Lune) la première éclipse, qui a lieu avant le passage au noeud appartient à la partie décroissante de sa suite longue et la seconde éclipse appartient à la partie croissante de sa suite longue. Dans le cas d'un triplet d'éclipses, la première appartient à la fin de la partie décroissante de la suite longue qui la contient, la dernière appartient au début de la partie croissante de la suite longue qui la contient et l'éclipse médiane se trouve au voisinage du maximum de sa suite longue.
En savoir plus: Exemple de saros, exemple de suite longue
 En savoir plus
En savoir plus
Le tableau suivant donne la liste des éclipses de la suite longue contenant l'éclipse du 31 mai 2003. On donne successivement le numéro de l'éclipse dans la suite longue, le type d'éclipse, la date de l'éclipse, sa magnitude et la durée maximale de la phase centrale lorsque cette phase existe.
| n° type |
date |
magnitude |
durée |
| 1P |
12/101624 |
0.0085968 |
|
| 2P |
23/10/1642 |
0.0548679 |
|
| 3P |
03/11/1660 |
0.0896182 |
|
| 4P |
14/11/1678 |
0.1146153 |
|
| 5P |
24/11/1696 |
0.1316624 |
|
| 6P |
07/12/1714 |
0.1419092 |
|
| 7P |
17/12/1732 |
0.1469513 |
|
| 8P |
28/12/1750 |
0.1505860 |
|
| 9P |
08/01/1769 |
0.1530884 |
|
| 10P |
19/01/1787 |
0.1591577 |
|
| 11P |
30/01/1805 |
0.1675941 |
|
| 12P |
11/02/1823 |
0.1857746 |
|
| 13P |
21/02/1841 |
0.2097100 |
|
| 14P |
04/03/1859 |
0.2462690 |
|
| 15P |
15/03/1877 |
0.2919636 |
|
| 16P |
26/03/1895 |
0.3533467 |
|
| 17P |
06/04/1913 |
0.5110283 |
|
| 18P |
17/04/1931 - 18/04/1931 |
0.5110283 |
|
| 19P |
28/04/1949 |
0.6095708 |
|
| 20P |
09/05/1967 |
0.7205292 |
|
| 21P |
19/05/1985 |
0.8411277 |
|
| 22A |
31/05/2003 |
0.9696001 |
03m34.08s |
| 23A |
10/06/2021 |
0.9721316 |
03m47.99s |
| 24A |
21/06/2039 |
0.9730915 |
04M01.45S |
| 25A |
01/07/2057 - 02/07/2057 |
0.9737206 |
04m40.41s |
| 26A |
13/07/2075 |
0.9737206 |
04m40.41s |
| 27A |
23/07/2093 |
0.9735538 |
05m06.77s |
| 28A |
04/08/2111 |
0.9731384 |
05m36.78s |
| 29A |
14/08/2129 - 15/08/2129 |
0.9724857 |
06m09.32s |
| 30A |
26/08/2147 |
0.9716470 |
06m42.98s |
| 31A |
05/09/2165 |
0.9706588 |
07m15.78s |
| 32A |
16/09/2183 - 17/09/2183 |
0.9695596 |
07m46.87s |
| 33A |
28/09/2201 |
0.9684309 |
08m14.61s |
| 34A |
09/10/2219 |
0.9672517 |
08m39.72s |
| 35A |
19/10/2237 |
0.9661547 |
09m00.30s |
| 36A |
30/10/2255 - 31/10/2255 |
0.9651065 |
09m17.21s |
| 37A |
10/11/2273 |
0.9642541 |
09m28.20s |
| 38A |
21/11/2291 |
0.9635287 |
09m34.68s |
| 39A |
02/12/2309 - 03/12/2309 |
0.9630803 |
09m34.31s |
| 40A |
14/12/2327 |
0.9628599 |
09m28.43s |
| 41A |
24/12/2345 |
0.9629606 |
09m15.58s |
| 42A |
04/01/2364 -05/01/2364 |
0;9633421 |
08m57.77s |
| 43A |
15/01/2382 |
0.9640683 |
08m34.41s |
| 44A |
26/01/2400 |
0.9651082 |
08m07.46s |
| 45A |
05/02/2418 - 06/02/2418 |
0.9664621 |
07m37.67s |
| 46A |
17/02/2454 |
0.9681073 |
07m06.45s |
| 47A |
27/02/2454 |
0.9700297 |
06m34.42s |
| 48A |
09/03/2472 - 10/03/2472 |
0.9721718 |
06m02.57s |
| 49A |
21/03/2490 |
0.9745093 |
05m31.07s |
| 50A |
01/04/2508 |
0.9769654 |
05m00.43s |
| 51A |
12/04/2526 -13/04/2526 |
0.9795505 |
04m29.66s |
| 52A |
23/04/2544 |
0.9821258 |
03m59.66s |
| 53A |
04/05/2562 |
0.9847154 |
03m29.01s |
| 54A |
14/05/2580 - 15/05/2580 |
0.9871679 |
02m58.81s |
| 55A |
26/05/2598 |
0.9895234 |
02m27.78s |
| 56A |
06/06/2616 |
0.9916211 |
01m58.16s |
| 57A |
17/06/2634 |
0.9935042 |
01m29.84s |
| 58A |
27/06/2652 - 28/06/2652 |
0.9935042 |
01m29.84s |
| 59A |
09/07/26700.9961687 |
0.9961687 |
00m47.26s |
| 60A |
19/07/2688 |
0.9961687 |
00m47.26s |
| 61A |
31/07/2706 -01/08/2706 |
0.9960352 |
00m36.88s |
| 62P |
11/08/2724 |
0.8822576 |
|
| 63P |
22/08/2742 |
0.7560645 |
|
| 64P |
01/09/2760 |
0.6399250 |
|
| 65P |
13/09/2778 |
0.5318151 |
|
| 66P |
23/09/2796 |
0.4338706 |
|
| 67P |
04/10/2814 |
0.3469499 |
|
| 68P |
15/10/2832 |
0.2725393 |
|
| 69P |
26/10/2850 |
0.2098505 |
|
| 70P |
05/11/2868 |
0.1587829 |
|
| 71P |
17/11/2886 |
0.1194801 |
|
| 72P |
28/11/2904 |
0.0907818 |
|
| 73P |
09/12/2922 |
0.0696946 |
|
| 74P |
20/12/2940 |
0.0570489 |
|
| 75P |
31/12/2958 |
0.0487713 |
|
| 76P |
10/01/2977 |
0.0452276 |
|
| 77P |
22/01/2995 |
0.0403169 |
|
En savoir plus: Exemple de saros-2
 En savoir plus
En savoir plus
On remarque que cette suite n'est pas complète, en effet le canon d'éclipse de l'IMCCE s'arrête en 2999, il y a probablement des éclipses de la suite qui sont postérieures à cette date. Malgré cela on dépasse la valeur moyenne de 72 éclipses. Et l'on est assez loin des valeurs moyennes, ainsi le nombre d'éclipses partielles de la partie croissante est de 21, la moyenne donne 12 ! On constate également que toutes les éclipses centrales sont des éclipses annulaires, donc l'arc parcouru par les conjonctions lunaires est au voisinage de l'apogée. L'éclipse du 31 mai 2003 est la première éclipse centrale de la partie croissante de la suite, on peut donc en déduire qu'elle a lieu après le passage au noeud et relativement longtemps après ce passage. De plus elle est proche d'un des pôles terrestres. On ne peut pas savoir si la suite est au noeud ascendant ou descendant de l'orbite lunaire. Pour cela il suffit de connaître la latitude de la Lune à la conjonction pour une seule éclipse de la suite. Cette latitude est positive pour l'éclipse du 31 mai donc cette suite longue est au noeud ascendant et l'éclipse du 31 mai 2003 est proche du pôle nord terrestre et les éclipses de la suite vont parcourir le globe terrestre du nord au sud.
Les éphémérides de la Lune nous donnent les informations suivantes :
- le 28/05/2003 à 13h 04m 44s UT : la Lune à l'apogée (distance maximale à la Terre) d=406168 km, diamétre. apparent. =29.5'.
- le 30/05/2003 à 08h 32m 17s UT : la Lune passe par le noeud ascendant de son orbite, long. moyenne = +59° 30,9'.
- le 31/05/2003 à 04h 08m 18s UT : maximum de l'éclipse annulaire de Soleil.
- le 31/05/2003 à 04h 19m 51s UT : Nouvelle Lune.
On constate que le maximum de l'éclipse a bien lieu entre le passage et la conjonction, qu'il est proche de la conjonction (11m 33s) mais éloigné du passage au noeud (19h 36m 1s). L'éclipse est proche du passage de la Lune à l'apogée elle est donc annulaire.
Les éclipses anciennes
Introduction
 Introduction
Introduction
Cette section traite des éclipses anciennes de Soleil et explique comment on utilise ces éclipses pour déterminer le ralentissement de la révolution terrestre.
Nous donnons un historique des prédictions des éclipses anciennes et nous donnons les possibilités des prédictions au fur et à mesure que les connaissances de l'orbite lunaire et de la cartographie évoluent. Ces propos sont illustrés par les cartes des lignes de visibilité des éclipses anciennes calculées avec les théories actuelles.
Le ralentissement de la Terre
Aussitôt que les astronomes eurent à leur disposition des théories de la Lune et du Soleil suffisamment précises, ils essayèrent de calculer et de tracer les zones de visibilité des éclipses anciennes décrites dans les textes antiques. Ils trouvèrent bien les éclipses de Soleil aux bonnes dates, mais ils s'aperçurent que les zones de visibilité qu'ils calculaient ne correspondaient pas aux zones d'observation des l'éclipses. E. Halley en 1693, puis R. Dunthorne en 1749, avancèrent l'idée que la Lune n'était pas à sa bonne position. Pour rendre cohérents les calculs d'éclipses et les observations on introduisit une accélération séculaire dans la théorie de la longitude de la Lune. Par la suite les mécaniciens célestes essayèrent de trouver une explication théorique à ce phénomène. Mais ils trouvèrent des explications théoriques qui n'expliquaient qu'en partie la valeur de cette accélération. En 1866, W. Ferrel et Delaunay vont émettre l'hypothèse d'un ralentissement de la rotation terrestre sous l'effet des marées océaniques, ce ralentissement contrebalancerait l'accélération qui apparaît dans l'observation du mouvement de la Lune. Ce ralentissement fut mis en évidence par Spencer Jones en 1926 et 1939, mais il faudra attendre la deuxième moitié du XXe siècle pour que l'on considère le phénomène réciproque, à savoir, l'influence des marées océaniques sur l'orbite lunaire et que l'on définisse complètement le problème. En réalité, l'accélération séculaire observée dans le mouvement de la Lune est la combinaison de trois termes : une accélération séculaire gravitationnelle due aux perturbations planétaires, une accélération séculaire due aux marées océaniques et une accélération séculaire fictive due au ralentissement de la rotation terrestre. Cette dernière accélération disparaît lorsqu'on utilise une échelle de temps uniforme (non liée à la rotation de la Terre). L'accélération séculaire gravitationnelle se calcule à partir des perturbations planétaires, l'accélération séculaire due aux marées océaniques se calcule à partir des mesures lasers des distances Terre-Lune. Le ralentissement de la rotation terrestre se calcule grâce aux éclipses anciennes.
Les échelles de temps
La rotation de la Terre autour de son axe a été longtemps considérée comme uniforme et a fourni une échelle de temps unique, le Temps universel (UT ou TU). La mise en évidence du ralentissement de la rotation terrestre par Spencer Jones a rendu nécessaire l'introduction à partir de 1960 d'une nouvelle échelle de temps, le Temps des éphémérides (TE). Cette échelle de temps est fonction de la révolution de la Terre autour du Soleil, cette révolution est très stable et elle fournit une meilleure réalisation d'un temps uniforme. Depuis 1967, cette échelle de temps a été remplacée par une échelle encore plus stable le Temps atomique international (TAI). Le temps civil actuel est encore basé sur la rotation de la Terre, il porte le nom de Temps universel coordonné (UTC) et n'est donc pas un temps uniforme.
L'usage des éclipses anciennes
Les théories des corps du système solaire, utilisent comme argument du temps, une échelle de temps uniforme liée au Temps atomique international appelée Temps Terrestre (TT). Pour connaître la portion du globe terrestre concerné par une éclipse, il faut connaître l'écart entre cette échelle de temps (TT) et l'échelle de temps non uniforme liée à la rotation de la Terre, le Temps universel (TU). Inversement lors d'une éclipse ancienne, l'écart entre la zone de visibilité calculée avec le Temps terrestre uniforme et les lieux d'observations effectifs de l'éclipse nous donne une approximation de l'écart (TT-TU) entre les deux échelles de temps. Un travail très important, portant sur de très nombreuses éclipses de Lune et de Soleil allant de l'an 763 avant J.-C. jusqu'à nos jours a été réalisé par Richard Stephenson et a permis de modéliser, pour le passé, les écarts entre le Temps Terrestre et le Temps universel.
Les sources anciennes
Les éclipses anciennes, de Lune et de Soleil, proviennent de quatre sources principales : les Babyloniens de 700 avant J.-C. à 50 avant J.-C., les Chinois de 700 avant J.-C. à 1500 après J.-C., les Européens de 500 avant J.-C. à 1 600 après J.-C. et les Arabes de 800 après J.-C. à 1 300 après J.-C. Certaines sources, bien que remontant très loin dans le temps, n'ont été connues que très récemment. C'est le cas notamment des sources babyloniennes et assyriennes que l'on ne sait déchiffrer que depuis le milieu du XIXe siècle.
Un des premiers astronomes à répertorier les éclipses anciennes fut Claude Ptolémée (milieu du IIe siècle), à cette occasion il créa une chronologie, l'ère de Nabonassar (le vrai nom est Nabu-nasir) qui débute en l'an 747 avant J.-C. et qui utilise l'année vague égyptienne de 365 jours. Ptolémée cite dans l'Almageste 10 éclipses de Lune observées par les Babyloniens et aucune éclipse de Soleil, les plus vieilles éclipses de Lune datant de 721 et 720 avant J.-C. Toutes les autres éclipses de Soleil et de Lune observées par les Babyloniens ou les Assyriens proviennent de tablettes écrites en caractères cunéiformes.
Les sources anciennes-2
La datation exacte de ces éclipses anciennes n'était pas une chose facile à réaliser avant que l'on ne connaisse le ralentissement de la rotation terrestre. En effet pour les dates indiquées, les éclipses calculées ne passaient pas par les lieux d'observations. Par exemple dans le cas de l'éclipse dite de Thalès, éclipse qui selon la légende rapportée par Hérodote dans l'Enquête, aurait été prédite aux Ioniens par Thalès, les astronomes et les historiens ont longtemps hésité entre plusieurs dates. Ainsi Eusèbe et Cicéron la plaçait en -584 (585 avant J.-C.), Scaliger en -582 (583 avant J.-C.) et Arago en -609 (610 avant J.-C.) Les astronomes anglais Airy et Fotheringham hésitèrent entre l'éclipse du 17 mai -602 (603 avant J.-C.) et celle du 28 mai -584 (585 avant J.-C.) avec une préférence pour la deuxième date. De nos jours, la bonne connaissance de l'écart entre le TT et le TU nous permet de confirmer la deuxième date, l'éclipse de -584 passant sur l'Asie Mineure.
La figure ci-contre nous montre les tracés des bandes de centralité des éclipses du 24 mai -584 et du 18 mai -602, nous avons tracé également les bandes de totalité des éclipses situées trois et six saros avant l'éclipse de -584. Certains historiens avaient émis, à tort, l'hypothèse que la prédiction de Thalès était possible car il aurait eu connaissance de l'éclipse homologue ayant eu lieu trois saros plus tôt. Comme on le constate cette éclipse passe bien plus au nord, suite au décalage en latitudes des éclipses homologues des suites longues d'éclipses.
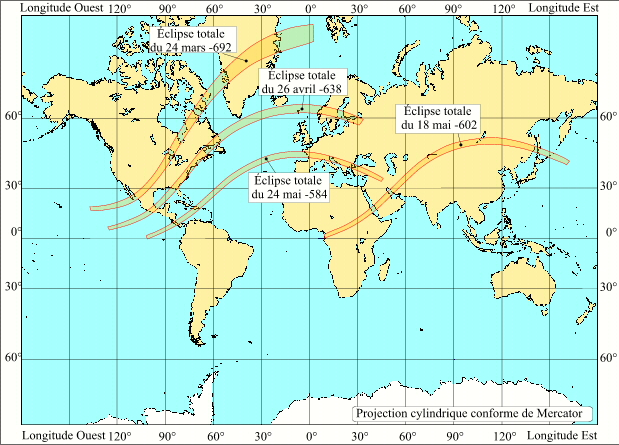
L'éclipse de Thalès et les éclipses homologues
Crédit : IMCCE/Patrick Rocher
Exemple de la détermination du ralentissement de la rotation terrestre
L'éclipse de -135 à Babylone
L'éclipse du Soleil du 15 avril -135 (136 avant J.-C.) est décrite dans deux textes cunéiformes écrits sur des tablettes d'argile se trouvant au British Museum. Outre la mention de l'éclipse, un des textes atteste la visibilité des planètes Mercure, Vénus et Jupiter au moment de l'éclipse. Si l'on ne tient pas compte du ralentissement de la Terre, la bande de centralité passe sur le sud de la France et l'Afrique du Nord. Pour faire passer l'éclipse, donc la bande de centralité sur Babylone, nous avons pris une valeur de la différence Temps terrestre moins Temps universel égale à 3h 14m 23s.
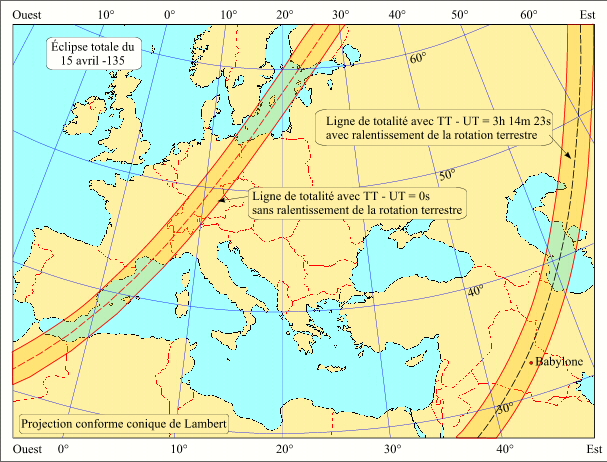
Crédit : IMCCE/Patrick Rocher
La prédiction des éclipses
Une simple observation d'éclipses permet de constater que les éclipses de Lune ont lieu uniquement à la pleine Lune et que les éclipses de Soleil ont lieu uniquement à la nouvelle Lune. La probabilité d'observer une éclipse de Lune en un lieu donné est beaucoup plus forte que la probabilité d'observer une éclipse de Soleil. On pense que les Babyloniens surent très tôt que les éclipses de Lune étaient séparées par cinq ou six lunaisons. Une des plus vieilles prédictions que l'on ait retrouvée date de 731 avant J.-C. et concerne l'éclipse de Lune du 9 avril 731 avant J.-C., le texte précise même que l'éclipse ne sera pas observable car la Lune ne sera pas levée. Des tablettes babyloniennes datant de 475 avant J.-C., contenant des éphémérides de la Lune, donnent dans une colonne un paramètre, qui correspond à la distance entre le centre de la Lune et le centre du cône d'ombre de la Terre, et qui permet de calculer la possibilité des éclipses de Lune. Sur d'autres tablettes figurent également des prédictions d'éclipses de Lune sur une période de 126 ans répartie en périodes de 223 lunaisons correspondant à la période de récurrence des éclipses. Dans chaque saros, 38 éclipses de Lune sont réparties en cinq suites courtes de 8,8,7,8 et 7 éclipses, les éclipses étant espacées entre elles dans les suites par six lunaisons et les suites courtes étant espacées entre elles par cinq lunaisons.
En Chine, on a trouvé les règles du saros chinois pour déterminer les éclipses de Lune dans des textes datant de l'époque de la période des Hans. On ne sait pas si la prédiction des éclipses de Soleil à l'aide du saros date des mêmes époques. La vérification par l'observation de la pertinence du saros pour les éclipses de Soleil étant quasi impossible en raison de la très faible probabilité d'observer une éclipse de Soleil.
Il ne faut surtout pas perdre de vue les faits suivants : le saros permet uniquement de déterminer la date d'une éclipse de Soleil, il ne permet pas de savoir où l'éclipse est observable. La détermination de la visibilité d'une éclipse de Soleil, en un lieu donné, nécessite la connaissance de la parallaxe lunaire et de la position de la Lune au demi-degré près, choses impossibles avant Ptolémée donc avant le milieu du IIe siècle.
Intérêt scientifique des éclipses de Soleil
La liste suivante contient une série de découvertes scientifiques liées aux éclipses de Soleil depuis le XIXe siècle :
- En 1836 : Bailly donne une première description des points brillants qui apparaissent en début et en fin de la totalité.
- En 1842 : Baily donne le nom à la couronne solaire et attribue la couronne au Soleil, et non pas à la Lune.
- En 1851 (28/07) : première photographie d'une éclipse de Soleil (daguerréotype).
- En 1860 (18/07) : première photographie montrant des protubérances solaires, les protubérances appartiennent bien au Soleil, durant cette éclipse on mis également en évidence la polarisation radiale de la lumière coronale.
- En 1868 (18/08) : début de l'analyse spectrale de la couronne et découverte de l'hélium (Janssen, Rayet et Pogson), l'hélium ne sera découvert sur Terre par Ramsay qu'en 1895.
- En 1869 : découverte d'une raie d'émission verte, le nouveau corps est appelé le coronium, ce nouveau corps n'existe pas, en fait, on avait observé le spectre d'éléments lourds fortement ionisés.
- En 1870 : découverte du spectre-éclair par Young, au moment de la totalité le spectre ordinaire du Soleil, avec ses raies sombres, disparaît et est remplacé par une multitude de raies brillantes.
- En 1872 : première observation des plumes, houppe des rayons polaires de la couronne, qui évoquent l'idée des lignes d'un champ magnétique.
- En 1878 : observations de rayons coronaux jusqu'à 6° du Soleil et connexion de la couronne interne (dite couronne K) avec la lumière zodiacale.
Intérêt scientifique des éclipses de Soleil-2
- 1901-1905-1908 : pour expliquer l'avance du périhélie de Mercure, recherche infructueuse durant les éclipses, d'une nouvelle planète proche du Soleil.
- 1919 (19/05) : tentative de vérification de la relativité générale (courbure de l'espace) au voisinage du Soleil, les résultats de cette expérience, tout comme ceux de celle de 1922, ne sont pas probants.
- 1930 : l'invention du coronographe par B. Lyot permet d'observer la couronne solaire et les protubérances en dehors des éclipses totales.
- 1995 : lancement du satellite SoHO (Solar and Heliocentric Observatory) vers le point de Lagrange Terre-Soleil avec plusieurs coronographes équipés de caméra CCD pour l'imagerie permettant l'observation continue du Soleil et de sa couronne.
Malgré la très forte évolution technologique qui permet de nos jours de suivre l'état du Soleil en temps réel, les éclipses totales de Soleil sont encore indispensables à l'étude de la basse couronne. En effet pour des raisons thermiques les coronographes qu'ils soient embarqués dans des sondes spatiales ou qu'ils soient à Terre, ont un diamètre trop important pour permettre la visualisation de la base couronne solaire.
Les éclipses de Lune
Auteur: P. Rocher - IMCCE- Observatoire de Paris
Introduction
 Introduction
Introduction
Ce chapitre porte sur les éclipses de Lune, nous allons reprendre une étude analogue à celle faite pour les éclipses de Soleil. Une grande partie des notions nécessaires pour cette étude a donc été développée dans les chapitres sur les éclipses de Soleil : le mouvement de la Terre, le mouvement de la Lune, les révolutions tropique, synodique, draconitique et anomaslistique, la notion de saison d'éclipses et de Saros. Nous insisterons particulièrement sur les différences entre les deux types d'éclipses.
 Prérequis
Prérequis
Il est vivement conseillé de lire le cours sur les mouvement de la Terre et de la Lune.
La géometrie des éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section, nous abordons l'aspect géométrique des éclipses de Lune : la taille des cônes d'ombre et de pénombre de la Terre au niveau de l'orbite lunaire. Puis nous définissons les différents types d'éclipses de Lune, les caractéristiques des cônes d'ombres et de pénombres, les effets géométriques et lumineux de l'athmosphère terrestre. Nous donnons ensuite la définition de la grandeur d'une éclipse de Lune et nous présentons les différents paramètres figurant dans les prédictions d'éclipse de Lune (avec un exemple). Nous terminons en présentant les zones de visibilité des éclipses de Lune et leurs représentations sur une carte en projection de Mercator.
Le cône d'ombre et le cône de pénombre
La Terre, éclairée par le Soleil, donne naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de la Terre constitue l'axe de ces cônes. Le sommet Sp du cône de pénombre est situé sur cet axe entre le Soleil et la Terre, et le sommet So du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport à la Terre. Le cône d'ombre est construit à l'aide des tangentes extérieures aux sphères solaire et terrestre, le cône de pénombre est construit à partir des tangentes intérieures aux sphères solaire et terrestre.
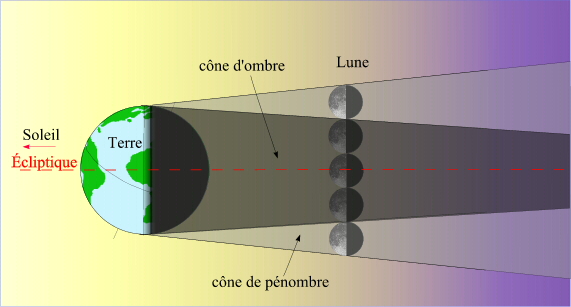
Cônes d'ombre et de pénombre.
Crédit : IMCCE/Patrick Rocher
La distance entre le sommet du cône d'ombre et le centre de la Terre varie en fonction de la distance Terre-Soleil. Elle est maximale, environ 231 rayons terrestres, lorsque la Terre est à son aphélie (actuellement vers le 4 juillet). Elle est minimale, environ 221 rayons terrestres, lorsque la Terre est à son périhélie (actuellement vers le 4 janvier). La Terre étant environ quatre fois plus large que la Lune, son ombre est également quatre fois plus longue. En cas d'éclipse de Lune, la Lune traverse le cône d'ombre terrestre au quart de sa longueur depuis la Terre, car la longueur Terre-Lune est égale à la longueur du cône d'ombre de la Lune. En cet endroit la largeur de la section du cône d'ombre de la Terre est de l'ordre des trois quarts de sa base, donc des trois quarts du diamètre terrestre, soit environ trois disques lunaires comme indiqué sur la figure ci-dessus.
De même la taille de la largeur de la couronne de pénombre de la Terre, à l'endroit où elle est traversée par la Lune est simple à évaluer. En effet, comme on le voit sur la figure ci-dessous c'est la largeur de la Lune elle-même, l'angle p des tangentes sud est égal au diamètre apparent du Soleil, qui est lui-même presque égal au diamètre apparent de la Lune. Donc une éclipse de Lune par la pénombre peut être totale.
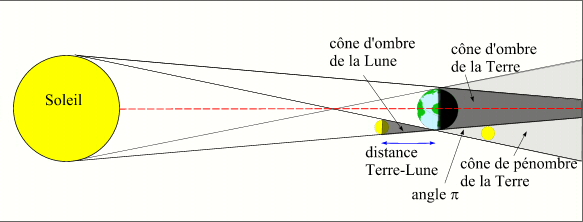
Cônes d'ombre et de pénombre.
Crédit : IMCCE/Patrick Rocher
 Remarque
Remarque
Sur cette figure les proportions ne sont pas respectées, le Soleil devrait être 400 fois plus gros que la Lune et 400 fois plus loin.
Les différents types d'éclipses de Lune
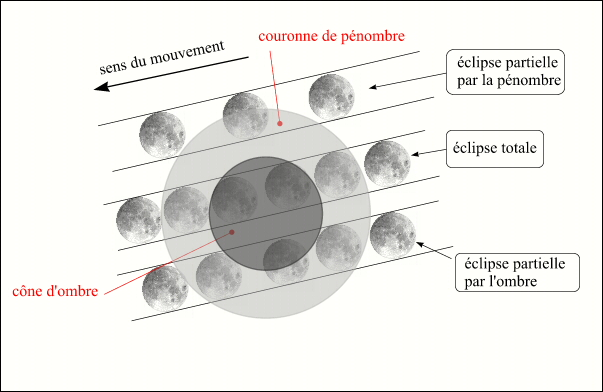
Les différents types d'éclipses de Lune
Crédit : IMCCE/Patrick Rocher
Comme nous l'avons vu précédemment, la section du cône d'ombre au niveau de l'orbite de la Lune est largement supérieure au diamètre apparent de la Lune (environ trois diamètres lunaires), la Lune peut donc être totalement éclipsée par l'ombre de la Terre, dans ce cas l'éclipse de Lune est dite totale.
Lorsqu'une partie seulement de la Lune passe dans le cône d'ombre de la Terre, la Lune n'est que partiellement éclipsée, l'éclipse est dite partielle par l'ombre.
Nous avons vu également que la taille de la couronne de pénombre était de la taille du diamètre apparent du Soleil et pouvait être supérieure au diamètre apparent de la Lune (Terre au périhélie et Lune à l'apogée). Dans ce cas la Lune peut passer entièrement dans la couronne de pénombre, dans ce cas l'éclipse de Lune est dite totale par la pénombre. Lorsque la Lune passe partiellement dans la couronne de pénombre il y a éclipse partielle de la Lune par la pénombre.
Caractéristiques des cônes d'ombre et de pénombre
Comme nous l'avons déjà vu la distance entre le centre de la Terre et le sommet du cône d'ombre et donc sa largeur varie en fonction de la distance Terre-Soleil. Elle vaut environ 231 rayons terrestres lorsque la Terre est à l'aphélie et elle vaut 221 rayons terrestres lorsque la Terre est à son périhélie.
De même la distance entre le sommet du cône de pénombre et le centre de la Terre dépend de la distance Terre-Soleil, elle est maximale, environ 216 rayons terrestres lorsque la Terre est à son aphélie et elle est minimale, environ 209 rayons terrestres lorsque la Terre est à son périhélie.
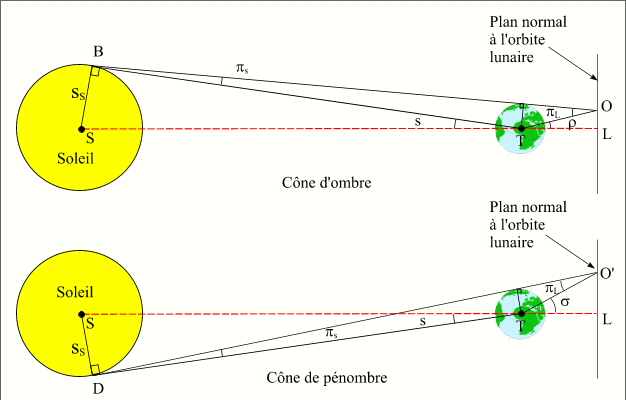
Demi-diamètres apparents géocentriques de l'ombre et de la pénombre
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-dessus le demi-diamètre apparent géocentrique de la section de l'ombre de la Terre par le plan normal à l'orbite lunaire est égal à l'angle ρ. L'ombre est déterminée par le cône de révolution d'axe ST et de génératrice BO, tangente extérieure au Soleil et à la Terre. Dans le triangle TOB la somme des angles intérieurs πs et πL est égale à la somme des angles extérieurs s et ρ. Or par définition πs est la parallaxe horizontale du Soleil, πL la parallaxe horizontale de la Lune et sS est le demi-diamètre apparent du Soleil. Donc ρ est égale à πs + πL - sS.
Ce demi-diamètre ρ est donc maximal lorsque la parallaxe lunaire πL est maximale et le demi-diamètre apparent πs est minimal (la parallaxe πs du Soleil étant pratiquement constante), c'est-à-dire lorsque la Lune est à son périgée et lorsque la Terre est à son aphélie. De même ce demi-diamètre ρ est minimal lorsque la parallaxe lunaire est minimale et le demi-diamètre apparent du Soleil est maximal, c'est-à-dire lorsque la Lune est à son apogée et la Terre à son périhélie.
On peut faire un raisonnement analogue pour le calcul du demi-diamètre apparent géocentrique du cône de pénombre σ. On trouve que σ est égal à πs + πL + sS. Ce demi-diamètre σ est donc maximal lorsque πL et sS sont maximales, donc lorsque la Lune est à son périgée et la Terre à son périhélie et il est minimal lorsque πL et sS sont minimales, donc lorsque la Lune est à son apogée et la Terre à son aphélie.
On remarquera que la largeur de la couronne de pénombre σ - ρ est bien égale au diamètre apparent du Soleil (2sS)
Le tableau suivant donne les valeurs extrêmes et moyennes du demi-diamètre sS apparent du Soleil, de la parallaxe lunaire πL et du demi-diamètre apparent sL de la Lune.
|
Terre périhélie
|
Moyenne
|
Terre aphélie
|
| sS
|
16'18" |
15'59.63" |
15'46" |
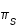
|
8.96" |
8.80" |
8.65" |
|
Lune périgée
|
Moyenne
|
Lune apogée
|
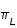
|
61' 27" |
57' 02,7" |
53' 53" |
| sL
|
16' 45" |
15' 32, 58" |
14' 41" |
Le tableau suivant donne les valeurs extrêmes et moyennes des demi-diamètres apparents géocentriques du cône d'ombre et du cône de pénombre.
|
Minimal |
Moyen |
Maximal |
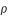
|
2263,96" = 37' 43,96" = 2,57 sL
|
2471,87" = 41' 11,87" = 2,65sL
|
2749,66" = 45' 49,66" = 2,74 sL
|
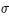
|
4187,65" = 1°09' 47,65" = 4,75 sL
|
4391,13" = 1° 13' 11,13" = 4,71 sL
|
4673,96" = 1° 17' 53,96" = 4,65 sL
|
On va voir que ces quantités doivent être augmentées de 1/73 en valeur relative pour ρ et de 1/128 en valeur relative pour σ afin de tenir compte de l'atmosphère terrestre.
Les effets géométriques de l'atmosphère terrestre
Contrairement aux éclipses de Soleil où l'ombre et la pénombre sont générées par un astre sans atmosphère, dans le cas des éclipses de Lune nous devons tenir compte des effets de l'atmosphère terrestre dans les calculs des limites de l'ombre et de la pénombre de la Terre.
Le trajet géométrique des rayons lumineux est soumis à la réfraction atmosphérique. L'atmosphère terrestre n'a pas de limite déterminée, on adopte une limite supérieure pour laquelle la réfraction atmosphérique n'a plus d'effets sensibles. Notre connaissance actuelle des répartitions des densités dans l'atmosphère suivant la verticale, ainsi que des mesures effectives de l'ombre de la Terre durant des éclipses de Lune nous conduisent à prendre 75km pour valeur limite. Cela se traduit dans les calculs par une augmentation du rayon terrestre de 1/85 en valeur relative. D'autre part la parallaxe de la Lune doit être une valeur moyenne et non pas la parallaxe horizontale, on prend donc la parallaxe lunaire à 45° de latitude, donc dans les calculs cela se traduit par une diminution de la parallaxe lunaire de 1/594 en valeur relative. Si l'on tient compte de ces deux corrections la valeur de la parallaxe horizontale doit être systématiquement augmentée de 1%. Cela se traduit par une augmentation du demi-diamètre géocentrique apparent ρ de l'ombre de 1/73 et une augmentation du demi-diamètre géocentrique σ apparent de la pénombre de 1/128.
Connaissant la valeur de la réfraction à l'horizon (environ 35') on peut calculer la distance du sommet cône d'ombre minimal, dans lequel on est sûr qu'il n'y aura aucune lumière solaire réfractée. On trouve une distance géocentrique du sommet de ce cône égale à environ 40 rayons terrestres. La distance Terre-Lune variant entre 56 et 63,8 rayons terrestres on est certain que la Lune recevra toujours des rayons solaires réfractés par l'atmosphère.
Les effets lumineux de l'atmosphère terrestre
L'atténuation atmosphérique
Comme nous venons de le voir, en raison de la réfraction et des distances Terre-Lune, la Lune éclipsée reçoit toujours des rayons lumineux réfractés par l'atmosphère terrestre.
La réfraction est également la cause d'un phénomène d'atténuation, dans la figure ci-dessous, considérons un rayon lumineux élémentaire, d'angle d
τ, issue du point S du disque solaire considéré plan (1). Ce rayon, suite à la réfraction atmosphérique, va illuminer la surface dS' située dans le plan de la Lune (2). En absence de réfraction il illuminerait la surface dS. Dans les deux cas le flux de lumière qui illumine ces deux surfaces est le même, les surfaces n'étant pas égales, la surface dS', supérieure à dS est moins éclairée.
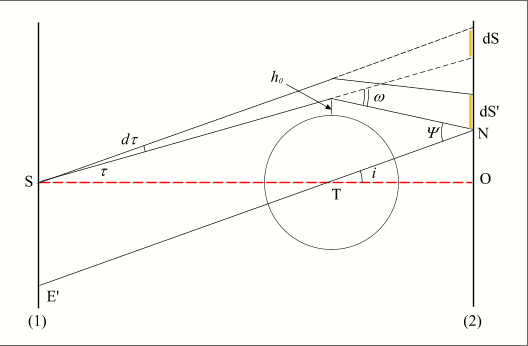
Crédit : IMCCE/Patrick Rocher
L'atténuation est donnée par le rapport des surfaces dS/dS' = Φ-1
Le terme Φ peut s'écrire sous la forme suivante :
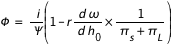
Cette formule comporte deux facteurs qui agissent en sens inverse, le premier diminue la surface éclairée (ds) et le deuxième élargit la surface éclairée (dS'), la combinaison des deux crée l'atténuation par réfraction. Pour imager notre propos considérons la figure suivante dans laquelle un rayon cylindrique de largeur dS est réfracté suivant une surface (ds) plus petite si on considère que la réfraction ne varie pas avec l'altitude (premier terme de la formule) et qui est réfracté suivant dS' si on considère que la réfraction décroît avec l'altitude (deuxième terme de la formule). Le premier terme fait donc bien croître l'illumination et le second la fait décroître.
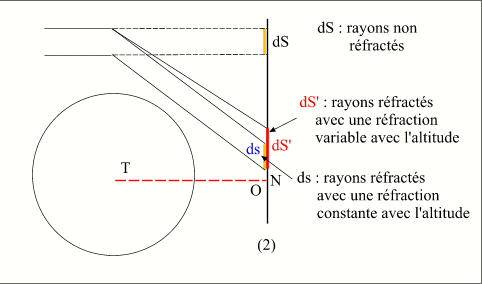
Crédit : IMCCE/Patrick Rocher
Si l'on exprime les variations de Φ en fonction de l'altitude h dans l'atmosphère, on s'aperçoit que c'est dans la haute atmosphère (troposphère) que l'atténuation est la plus appréciable malgré la faible valeur de la réfraction. Elle décroît ensuite jusqu'à la valeur un, pour une altitude h d'environ 2km, puis le phénomène s'amplifie et pour la valeur i=0 il y a focalisation. De plus on peut dire que l'atténuation par la réfraction est pratiquement neutre et que l'ombre est approximativement grise.
L'absorption atmosphérique
L'absorption atmosphérique est produite par la diffusion de la lumière par les molécules et les aérosols de l'air. L'absorption atmosphérique est très sensible à la longueur d'onde (c'est une loi en 1/λ
4). La lumière bleue est donc plus absorbée que la lumière rouge, cette absorption croît avec la largeur de la couche atmosphérique traversée, ce qui explique le rougeoiement du ciel au coucher du Soleil. Dans le cas des éclipses de Lune ce sont les rayons passant à faible altitude qui traversent la plus grande largeur d'atmosphère, ce sont donc ces rayons qui ont un maximum de lumière bleue absorbée et qui sont donc les plus rouges. Comme ce sont aussi ces rayons qui sont les plus réfractés, le centre de l'ombre aura un aspect rougeâtre.
Le degré d'absorption dépend également des conditions météorologiques, donc la luminosité de la partie centrale de l'ombre est très sensible aux conditions météorologiques régnant dans les couches atmosphériques traversées.
L'intensité lumineuse au centre du cône dépend également de la distance à laquelle se trouve la Lune, et les éclipses totales proches du périgée sont toujours plus sombres que les éclipses totales proches de l'apogée.
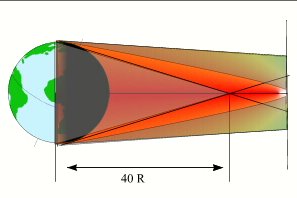
Limite des rayons réfractés
Crédit : IMCCE/Patrick Rocher
Grandeur d'une éclipse de Lune
La grandeur, ou magnitude, est un paramètre important des éclipses de Lune. Dans le cas des éclipses totales et partielles par l'ombre, elle est égale au rapport de la distance du bord de la Lune (A) le plus proche du centre du cône d'ombre au bord du cône d'ombre le plus près du centre de la Lune (B) sur le diamètre de la Lune (AC) et cela à l'instant du maximum de l'éclipse, c'est-à-dire à l'instant où la distance entre le centre de la Lune et le centre de l'ombre est minimale. Pour une éclipse par la pénombre la définition de la grandeur est identique, il suffit de remplacer le cône d'ombre par le cône de pénombre.
Dans le cas d'une éclipse par l'ombre on a : 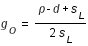
et dans le cas d'une éclipse par la pénombre on a 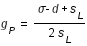
où d est la distance entre le centre de la Lune et le centre de l'ombre, sL le demi-diamètre lunaire, ρ et σ étant respectivement les demi-diamètres apparents de l'ombre et de la pénombre.
Compte tenu de cette définition, plus la grandeur d'une éclipse est importante plus la Lune passe près du centre du cône d'ombre. Les éclipses totales par l'ombre ou par la pénombre ont une grandeur supérieure à un et les éclipses partielles ont une grandeur inférieure à un. La grandeur d'une éclipse totale centrale est égale à 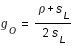 .
.
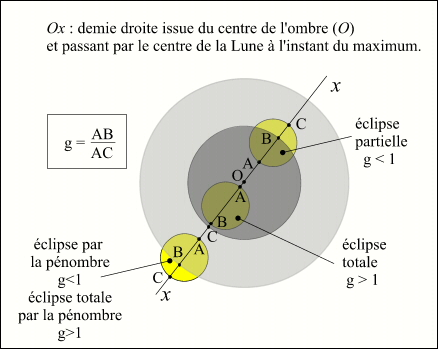
Grandeur des éclipses de Lune.
Crédit : IMCCE/Patrick Rocher
Sur le dessin ci-dessus, pour les éclipses par la pénombre B est l'intersection de Ox avec le bord de la pénombre. Pour les éclipses partielles et les éclipses totales B est l'intersection de Ox avec le bord de l'ombre. AC est le diamètre lunaire (2sL).
Les données fournies pour une éclipse de Lune
Pour chaque éclipse de Lune, on donne les instants des débuts et des fins des différentes phases. Ces instants, exprimés en Temps universel coordonné, sont les mêmes quel que soit le lieu d'observation, la visibilité des différentes phases est uniquement liée au fait que la Lune soit levée ou non aux instants considérés. On donne également la valeur de la grandeur de l'éclipse, parfois appelée magnitude.
Les différentes phases des éclipses de Lune sont les suivantes :
- L'entrée de la Lune dans la pénombre : c'est l'instant où le disque lunaire est tangent extérieur au cône de pénombre.
- L'entrée de la Lune dans l'ombre, uniquement les éclipses par l'ombre : c'est l'instant où le disque lunaire est tangent extérieur au cône d'ombre.
- Le commencement de la totalité, uniquement pour les éclipses totales par l'ombre : c'est l'instant où le disque lunaire est tangent intérieur au cône d'ombre.
- Le maximum de l'éclipse : c'est l'instant où la distance entre le centre du disque lunaire et le centre du cône d'ombre est minimale.
- La fin de la totalité, uniquement pour les éclipses totales par l'ombre : c'est l'instant où le disque lunaire est de nouveau tangent intérieur au cône d'ombre.
- La sortie de l'ombre, uniquement pour les éclipses par l'ombre : c'est l'instant où le disque lunaire est de nouveau tangent extérieur avec le cône d'ombre.
- La sortie de la pénombre : c'est l'instant où le disque lunaire est de nouveau tangent extérieur avec le cône de pénombre.
Pour chaque début et fin de phase on donne également l'angle au pôle des points de contacts, les points de contacts sont les points de tangences entre le disque lunaire et les cônes d'ombre et de pénombre. L'angle au pôle est l'angle formé par la direction du pôle nord céleste et la demi-droite issue du centre lunaire et passant par le point de tangence, cet angle est compté positivement vers l'ouest (donc dans le sens direct).
On fournit également avec ces valeurs les durées des différentes phases de l'éclipse.
- La durée totale de l'éclipse : intervalle de temps entre l'entrée et la sortie de la pénombre.
- La durée de la phase partielle : intervalle de temps entre l'entrée et la sortie de l'ombre.
- La durée de la totalité : intervalle de temps entre le début et la fin de la totalité.
On donne également les positions apparentes géocentriques du centre de l'ombre et du centre de la Lune pour l'instant du maximum de l'éclipse, ainsi que les valeurs de certains paramètres géométriques de l'éclipse.
- L'ascension droite géocentrique apparente du centre de l'ombre.
- La déclinaison géocentrique apparente du centre de l'ombre.
- Le diamètre apparent du cône d'ombre.
- Le diamètre apparent du cône de pénombre.
- La parallaxe équatoriale du Soleil.
- L'ascension droite géocentrique apparente du centre de la Lune.
- La déclinaison géocentrique apparente du centre de la Lune.
- Le diamètre apparent de la Lune.
- La parallaxe équatoriale de la Lune.
En savoir plus: Exemple de données
 En savoir plus: L'éclipse totale de Lune du 4 mai 2004
En savoir plus: L'éclipse totale de Lune du 4 mai 2004
Éléments à l'instant du maximum de l'éclipse
- Maximum de l'éclipse le 4 mai 2004 à 20h 30m 7,031s UTC
- Ascension droite du centre de l'ombre : 14h 48m 55,84s.
- Déclinaison du centre de l'ombre : -16° 14' 51,48".
- Diamètre du cône d'ombre : 91,16'
- Diamètre du cône de pénombre : 154,59'
- Parallaxe équatoriale du Soleil : 8,72".
- Ascension droite du centre de la Lune : 14h 48m 25,15s.
- Déclinaison du centre de la Lune : -16° 32' 22,88".
- Diamètre apparent de la Lune : 33,07'
- Parallaxe équatoriale de la Lune : + 1° 0' 40,81".
Circonstance de l'éclipse
| Phases |
Instant en UTC |
Longitude* |
Latitude* |
Angle au pôle |
| Entrée dans la pénombre |
le 4 à 17h 52,2m |
-89° 32,4' |
-15° 54,5' |
101,1° |
| Entrée dans l'ombre |
le 4 à 18h 48,5m |
-75° 58,7' |
-16° 8,1' |
95,0° |
| Début de la totalité |
le 4 à 19h 52,4m |
-60° 36,1' |
-16° 23,4' |
251,9° |
| Maximum de l'éclipse |
le 4 à 20h 30,1m |
-51° 31,1' |
-16° 32,4' |
202,8° |
| Fin de la totalité |
le 4 à 21h 7,9m |
-42° 25,9' |
-16° 41,3' |
153,6° |
| Sortie de l'ombre |
le 4 à 22h 11,8m |
-27° 3,5' |
-16° 56,4' |
310,6° |
| Sortie de la pénombre |
le 4 à 23h 8,0m |
-13° 31,3' |
-17° 9,5' |
304,4° |
(*) Dans ce tableau les longitudes et latitudes sont les coordonnées des lieux ayant la Lune au zénith à chaque phase, les longitudes sont comptées positivement vers l'ouest et négativement vers l'est.
On donne également la durée des différentes phases :
- Durée de l'éclipse : 5h 15m 50,50s.
- Durée de la phase partielle : 3h 23m 15,05s.
- Durée de la phase totale : 1h 15m 29,43s.
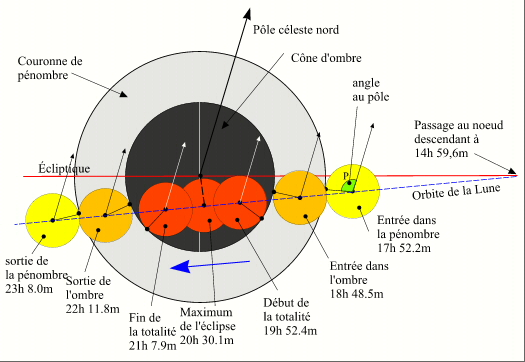
Phases de l'éclipse totale de Lune du 4 mai 2004.
Crédit : IMCCE/Patrick Rocher
Les éphémérides de la Lune donnent les renseignements supplémentaires suivants :
- le 04/05/2004 à 09h 19m 04s UT : la Lune entre dans la constellation de la Balance.
- le 04/05/2004 à 14h 59m 39s UT : la Lune passe par le nœud descendant de son orbite, long. moyenne = +221° 15,7'.
- le 04/05/2004 à 20h 33m 24s UT : Pleine Lune.
- le 06/05/2004 à 04h 31m 56s UT : la Lune au périgée (distance minimale à la Terre) d=359811 km, diam. app. =33.3'.
On constate que la Lune est passée par le nœud descendant de son orbite avant le début de l'éclipse, c'est donc une éclipse au nœud descendant, donc logiquement le maximum de l'éclipse, correspondant à la distance minimale du centre du disque lunaire au centre de l'ombre doit avoir lieu avant l'opposition (pleine Lune). Ce qui est bien le cas le maximum a lieu à 20h 30.1m et la pleine Lune a lieu à 20h 33,6m. De plus on constate que la Lune est proche de son périgée, donc sa vitesse angulaire est forte et son diamètre apparent est proche de son maximum. Donc la durée de l'éclipse est relativement courte (proche de 5h).
Zones de visibilité d'une éclipse de Lune
Comme nous l'avons déjà dit, pour qu'une éclipse de Lune soit visible en un lieu donné, il suffit que la Lune soit levée en ce lieu durant l'éclipse. La durée totale d'une éclipse pouvant atteindre plusieurs heures il y a obligatoirement des parties du globe terrestre qui ne verront qu'une partie de l'éclipse. Pour connaître les différents endroits du globe où une éclipse de Lune est visible, il suffit de tracer sur une carte les lieux où la Lune est à l'horizon à l'instant des débuts et des fins des différentes phases de l'éclipse. Sur ces courbes, une première moitié des lieux correspond à un lever de Lune et une seconde moitié des lieux correspond à un coucher de Lune. Tous les points du globe situés à l'est de la première moitié et à l'ouest de la seconde voient la Lune et donc la phase de l'éclipse correspondant.
Au maximum, il y a trois débuts et trois fins de phase pour une éclipse, on trace donc au plus six courbes de visibilité par éclipse et l'on utilise les notations suivantes :
- P1 : la limite de la région où l'on observe l'entrée dans la pénombre (pointillés larges),
- O1 : la limite de la région où l'on observe l'entrée dans l'ombre (pointillés normaux),
- T1 : la limite de la région où l'on observe l'entrée dans la totalité (petits pointillés),
- T2 : la limite de la région où l'on observe la fin de la totalité (petits pointillés),
- O2 : la limite de la région où l'on observe la sortie de l'ombre (pointillés normaux),
- P2 : la limite de la région où l'on observe la sortie de la pénombre (pointillés larges),
- V : la région de visibilité,
- I : la région d'invisibilité.
La lettre V indique la portion du globe terrestre où l'éclipse est visible (en totalité ou en partie) et la lettre I indique la portion du globe où l'éclipse n'est pas visible.
On utilise généralement une projection de Mercator, on s'arrange pour centrer la carte sur la zone de visibilité V de l'éclipse. Par exemple tous les lieux situés à l'intérieure de la courbe P1 contenant le symbole V voient l'entrée de la Lune dans la pénombre.
 Remarque
Remarque
Chaque courbe est le terminateur du lieu où la Lune est au zénith pour chaque début ou fin de phase, c'est pourquoi on fournit avec chaque instant correspondant aux débuts et aux fins de phase les coordonnées géographiques du lieu ayant la Lune au zénith, ces coordonnées permettent de tracer sur les cartes les terminateurs en question, c'est-à-dire les grands cercles de la sphère terrestre ayant pour pôles ces lieux.
En savoir plus: Carte de visibilité de l'éclipse totale du 4 mai 2002
 En savoir plus
En savoir plus
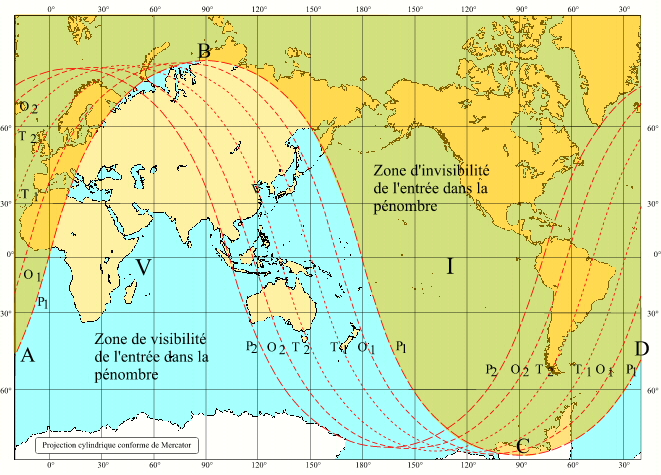
Carte de visibilité de l'éclipse totale de Lune du 4 mai 2002
Crédit : IMCCE/Patrick Rocher
Sur cette carte P1 indique les lieux où la Lune est à l'horizon au début de l'éclipse (entrée dans le cône de pénombre), la partie gauche AB et extrême droite CD de la courbe correspondent au lever de la Lune et la partie centrale BC de la courbe correspond au coucher de la Lune. Les lieux situés dans la zone de visibilité, en claire sur la carte verront le début de l'éclipse, les lieux de la partie ombrée ne verront pas le début de l'éclipse. On peut faire un raisonnement identique pour chacune des cinq autres courbes.
Explication de la visibilité de l'éclipse à Paris
Paris est à l'ouest des parties des courbes P1 et O1 correspondant au lever de la Lune aux instants des entrées dans la pénombre et dans l'ombre, on ne verra donc pas ces deux débuts de phase à Paris car la Lune n'y sera pas levée. Par contre Paris est à l'est de toutes les autres courbes, dont on verra toutes les autres phases de l'éclipse : ainsi la Lune se lèvera partiellement éclipsée par l'ombre de la Terre, puis on verra le début de la totalité, puis toute la phase totale puis la fin de la totalité et en fin les sorties de l'ombre et de la pénombre. On peut vérifier très simplement cette prédiction en comparant les instants des différentes phases de l'éclipse avec les heures du lever du Soleil à Paris ce jour. En effet comme nous sommes proches de la pleine Lune, la Lune se lève sensiblement lorsque le Soleil se couche vers 19h 9min UTC, or les deux premières phases qui débutent respectivement à 17h 52.2m UTC et à 18h 48.5m UTC ne seront effectivement pas visibles, par contre l'entrée dans l'ombre ayant lieu à 19h 52.4m UCT sera visible car la Lune sera levée. Les phases suivantes, jusqu'à la dernière phase (sortie de la pénombre) qui aura lieu à 23h 8m UTC donc en pleine nuit, seront visibles.
En conclusion on peut dire que pour connaître la visibilité d'une éclipse de Lune en un lieu quelconque il suffit de comparer les instants des différentes phases de l'éclipse avec les heures de nuit en ce lieu. Toutes les phases ayant lieu de nuit sont visibles.
Quand ont lieu les éclipses de Lune ?
Introduction
 Introduction
Introduction
Dans cette section nous abordons l'aspect dynamique des éclipses de Lune. Nous reparlons du mouvement de la ligne des noeuds de l'orbite lunaire et de la saison des éclipses, nous définissons de nouveau des critères en latitude et en longitude pour avoir une éclipse au voisinage de la pleine Lune. Nous étudions, comme pour les éclipses de Soleil, le nombre d'éclipses à chaque saison d'éclipse et l'évolution des éclipses saison après saison. Nous reprenons la prédiction des éclipses de Lune et de Soleil sur la période de 22 ans (1998-2020).
Le mouvement moyen de la ligne des noeuds
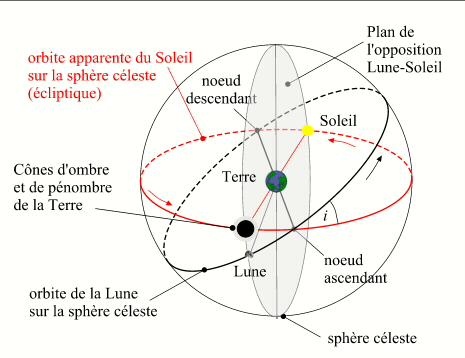
Opposition de la Lune et du Soleil : pleine Lune
Crédit : IMCCE/Patrick Rocher
Il y a éclipse de Lune lorsque la Lune passe dans le cône d'ombre ou dans le cône de pénombre de la Terre. Le Soleil, la Terre et la Lune sont alors presque alignés, et on est au voisinage de la pleine Lune (opposition). Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Lune à chaque pleine Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 17' sur le plan de l'orbite terrestre à la pleine Lune. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des nœuds et les intersections de cette droite avec l'orbite de la Lune sont appelées nœuds de l'orbite lunaire.
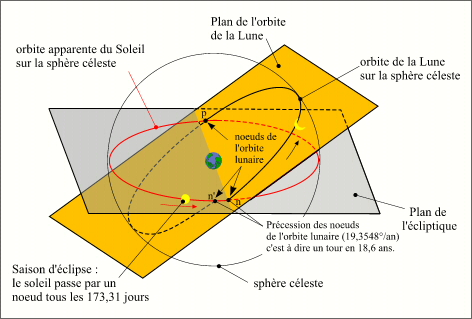
Orbites de la Lune, mouvement de la ligne des nœuds
Crédit : IMCCE/Patrick Rocher
Cette ligne des nœuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans, soit un déplacement de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc, dans le repère écliptique géocentrique, que la direction Soleil-Terre soit près de la ligne des nœuds lunaires au moment de la pleine Lune. Compte tenu du mouvement de précession des nœuds, le Soleil apparent passe par l'un des deux nœuds tous les 173,31 jours. Cette période porte le nom de saison d'éclipses. Il passe par le même nœud tous les 346,32 jours, cette période porte le nom d'année des éclipses.
En savoir plus: Le calcul de la saison des éclipses
 En savoir plus
En savoir plus
La direction Terre-Soleil est la direction du Soleil apparent vu depuis la Terre, elle fait donc 360° pendant une révolution sidérale de la Terre. La ligne des nœuds de l'orbite lunaire se déplace en moyenne de 19,3413618°/an dans le sens rétrograde. On a donc deux mouvements en sens contraire. La période T qui ramène le Soleil apparent dans la direction d'un même nœud de l'orbite lunaire est solution de l'équation suivante :
T . 360°/an + T . 19,3413618°/an = 360°
ce qui donne T = 360/(360 + 19,3413618) an = 0,9490133 an.
L'année sidérale étant égale à : an = 365,2563632 jours, T = 346,63 jours.
La saison des éclipses correspond à l'intervalle de temps mis par le Soleil apparent pour passer d'un nœud de l'orbite lunaire à l'autre, elle est donc égale à T/2 ~ 173,31 jours.
La valeur de cette période T nous permet de calculer la vitesse moyenne du Soleil apparent (ou de la Terre) dans un repère tournant lié à la ligne des nœuds de l'orbite lunaire. Par rapport à cette ligne des nœuds le Soleil apparent fait un tour de 360° en 346,63 jours, sa vitesse moyenne par rapport à la ligne des nœuds est donc de 360°/346,63j = 1,038°/jour.
En savoir plus: Le mouvement réel de la ligne des noeuds
 En savoir plus
En savoir plus
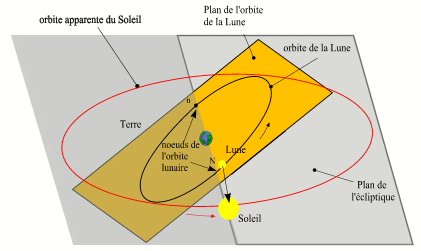
Système Terre - Lune - Soleil lorsque le Soleil est sur la ligne des nœuds
Crédit : IMCCE/Patrick Rocher
En réalité, le mouvement rétrograde de la ligne des nœuds présente des inégalités importantes. À certaines époques, sa vitesse est le double de la moyenne. À d'autres moments, sa vitesse est nulle, les nœuds sont alors stationnaires. Cela se produit aux voisinages du passage du Soleil dans la direction de la ligne des nœuds, donc au voisinage des éclipses de Soleil (et aussi de Lune). On peut expliquer ce phénomène de la manière suivante, lorsque le Soleil est sur la ligne des nœuds, il se trouve dans le plan de l'orbite de la Lune, la force perturbatrice du Soleil est alors comprise dans le plan de l'orbite de la Lune, donc la composante perpendiculaire à ce plan est nulle et ne "tire" pas sur le plan de l'orbite. Le fait que les nœuds soient quasi-stationnaires au moment des éclipses est très important, en effet les positions moyennes des nœuds sont alors presque égales aux positions vraies, donc dans l'étude des éclipses on peut utiliser le mouvement moyen des nœuds.
Le critère en latitude
On démontre qu'une éclipse de Lune se produira si, au moment de la pleine Lune (instant où la différence des longitudes géocentriques de la Lune et du Soleil est égale à 180°, c'est-à-dire au moment de l'opposition), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du cône d'ombre est inférieure à 1,41° (1° 25' 23"), elle se produira peut-être si elle est comprise entre 1,41° (1° 25' 23") et 1,59° (1°35' 40") et elle ne se produira pas si elle est supérieure à 1,59° (1° 35' 40").
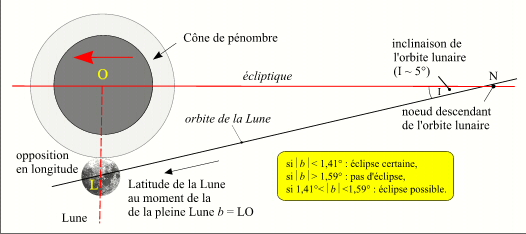
Critères en latitude pour les éclipses de Lune (vue depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-dessus, la distance minimale correspond à l'instant où pour le centre de la Terre, le centre de la Lune est le plus près possible du centre du cône d'ombre, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Lune on a toujours un des deux scénarios suivants :
- si l'éclipse a lieu avant le passage de la Lune au nœud, on observe d'abord l'opposition (pleine Lune), puis le maximum de l'éclipse, puis le passage au nœud,
- si l'éclipse a lieu après le passage de la Lune au nœud, on observe d'abord le passage au nœud, puis le maximum de l'éclipse et enfin l'opposition.
La géométrie de ce dessin montre également que plus l'opposition est proche du nœud, plus la distance minimale entre la Lune et le centre du cône d'ombre est petite et plus la grandeur (magnitude) de l'éclipse est grande. Ainsi, les éclipses par la pénombre correspondent à des oppositions situées loin des nœuds de l'orbite lunaire et les éclipses par l'ombre (partielles ou totales) correspondent à des oppositions proches des nœuds de l'orbite lunaire.
On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,89°) on a une éclipse par l'ombre avec certitude et pour quelle valeur de b (1,06°) on n'a pas d'éclipse par l'ombre avec certitude (mais une éclipse par la pénombre avec certitude); de même on peut déterminer pour quelle valeur de b (0,36°) on a une éclipse totale avec certitude et pour quelle valeur de b (0,53°) on n'a pas d'éclipse totale avec certitude, ces valeurs sont données dans le graphique ci-dessous.
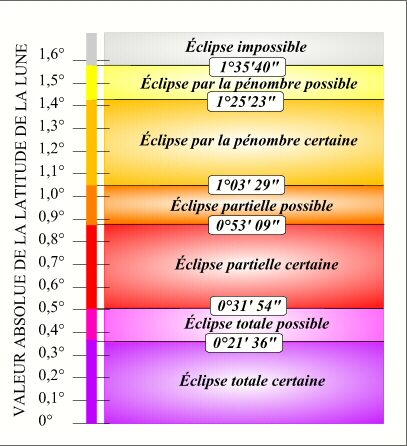
Crédit : IMCCE/Patrick Rocher
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Lune par la pénombre il faut que b soit inférieure à βm = 1,49°, pour avoir une éclipse de Lune par l'ombre il faut que b soit inférieure à βm = 0,96° et pour avoir une éclipse totale de Lune il faut que b soit inférieure à βm = 0,44°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses par la pénombre (36%), la proportion d'éclipses par l'ombre (64%) et la proportion d'éclipses totales (30%).
 Remarque
Remarque
Les bornes d'existence des éclipses de Lune : 1,41° (1° 25' 23") et 1,59° (1°35' 40") sont très proches des limites des éclipses de Soleil : 1,41° (1° 24' 37") et 1,59° (1°34' 46"). Les écarts sont de l'ordre de la minute de degré. Les bornes des éclipses de Lune sont un peu plus grandes que les bornes des éclipses de Soleil en raison de la réfraction atmosphérique.
En savoir plus: La démonstration du critère en latitude
 En savoir plus
En savoir plus
La démonstration est en tout point identique à la démonstration du critère en latitude des éclipses de Soleil, il suffit de remplacer la conjonction par l'opposition et le Soleil par les cônes d'ombre et de pénombre de la Terre.
Nous allons établir le critère en latitude dans le cas d'une éclipse au nœud ascendant de l'orbite lunaire, l'opposition ayant lieu avant le passage au nœud. La démonstration est identique pour un passage au nœud descendant ou avec une opposition située après le passage au nœud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
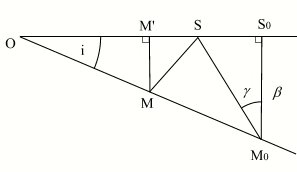
Critère en latitude
Crédit : IMCCE/Patrick Rocher
Soit M0 et S0 : les positions de la Lune et du centre du cône d'ombre à l'instant de l'opposition (pleine Lune) avant le passage de la Lune au nœud ascendant de son orbite.
M et S : les positions de la Lune et du centre du cône d'ombre à un instant t postérieur à l'opposition.
γ : l' angle S0M0S.
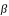 : la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
: la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
q : le rapport du mouvement en longitude de la Lune sur celui du centre du cône d'ombre (Soleil+180°).
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM et de le comparer à la somme des demi-diamètres géocentriques apparents des cônes d'ombre 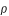 (et de pénombre
(et de pénombre 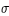 ) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
On a :
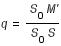 soit
soit 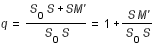
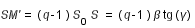 avec
avec 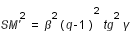
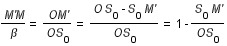
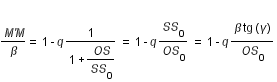
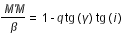
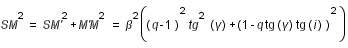 (1)
(1)
On introduit un angle auxiliaire i', tel que : 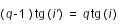
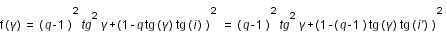
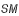 est minimum lorsque
est minimum lorsque 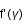 est nulle
est nulle
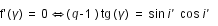 (2)
(2)
Ce qui correspond à : 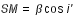 (3)
(3)
Cette distance correspond à une observation vue du centre de la Terre (coordonnées géocentriques).
En savoir plus: La démonstration du critère en latitude-2
 En savoir plus
En savoir plus
Il y a éclipse par la pénombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône de pénombre et de la Lune.
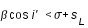
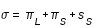
soit : 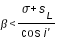 (4)
(4)
Il y a éclipse par l'ombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône d'ombre et de la Lune.
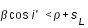
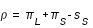
soit : 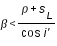 (5)
(5)
Il y a éclipse totale par l'ombre lorsque SM est inférieur à la différence des demi-diamètres apparents du cône d'ombre et de la Lune.
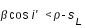
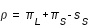
soit : 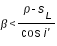 (6)
(6)
Il suffit alors de remplacer dans ces formules les paramètres par leurs valeurs extrêmes pour en déduire les critères en latitude.
Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.
|
maximum |
Minimum |
moyenne |
| q |
16,2 |
10,9 |
13,5 |
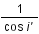
|
1,0052 |
1,0043 |
1,00472 |
Parallaxe Lune 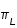
|
61' 27" |
53' 53" |
57' 2,70" |
Parallaxe Soleil 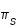
|
8,96" |
8,65" |
8,80" |
| 1/2 diamètre Lune sL
|
16' 45" |
14' 41" |
15' 32,58" |
| 1/2 diamètre Soleil sS
|
16' 18" |
15' 46" |
15' 59,63" |
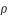 * * |
46' 27" |
38' 15" |
41' 45,73" |
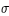 * * |
1° 18' 30" |
1° 10' 20" |
1° 13' 45" |
* Dans le calcul de ces valeurs on a tenu compte de la réfraction atmosphérique et de la parallaxe de la Lune à 45° de latitude en multipliant σ par (1+1/128) et ρ par (1+1/73).
Ainsi la valeur inférieure βMin du second membre de (4) est obtenue avec σ et sL minimales, la valeur supérieure βMax est obtenue avec σ et sL maximales et l'on obtient βMin=1°25'23" et βMax=1°35'40". Ce sont les limites d'existence des éclipses de Lune.
De même la valeur inférieure βMin du second membre de (5) est obtenue avec ρ et sL minimales, la valeur supérieure βMax est obtenue avec ρ et sL maximales et l'on obtient βMin=0°53'9,63" et ΔMax=1°3'28,6". Ce sont les limites d'existence des éclipses de Lune par l'ombre.
Et enfin la valeur inférieure βMin du second membre de (6) est obtenue avec ρ minimal et sL maximal, la valeur supérieure βMax est obtenue avec ρ maximal et sL minimal et l'on obtient βMin=0°21'35,52" et βMax=0°31'54,52". Ce sont les limites d'existence des éclipses totales de Lune.
Le critère en longitude
Le critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude de l'opposition Lune Soleil donc de la longitude du centre du cône d'ombre (Soleil +180°) par rapport au nœud de l'orbite lunaire. Ainsi il y aura éclipse si au moment de l'opposition en longitude, la différence de longitude entre le nœud de l'orbite lunaire et la longitude du centre du cône d'ombre est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit on a repris le même critère que dans le cas des éclipses de Soleil, en effet vu la faible différence des critères en latitude, on peut considérer que les critères en longitude sont identiques, en réalité les critères en longitude pour les éclipses de Lune sont un petit peu plus larges que les critères en longitude pour les éclipses de Soleil.
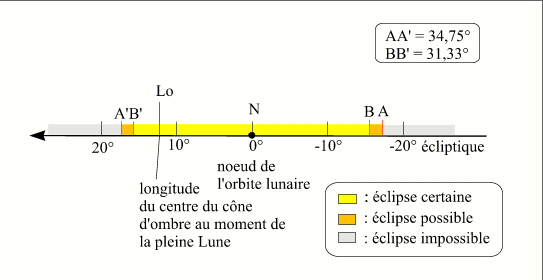
Critère en longitude pour les éclipses de Lune (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
La figure suivante représente le critère en longitude vu dans le repère géocentrique écliptique.
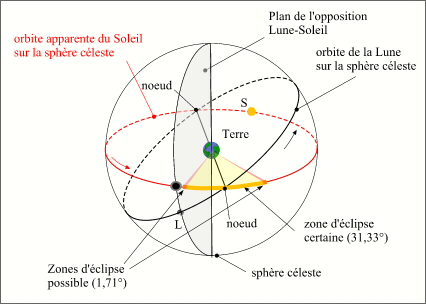
Critère en longitude pour les éclipses de Lune (vu depuis l'espace)
Crédit : IMCCE/Patrick Rocher
Nombre d'éclipses à chaque saison d'éclipse
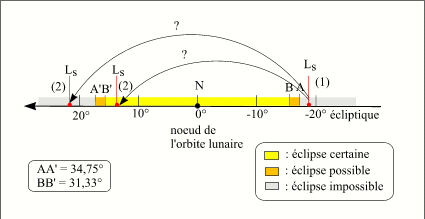
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
En étudiant la figure ci-dessus, on peut se poser la question suivante. Supposons que nous ayons une conjonction en longitude (1) juste avant le point A, la conjonction suivante (2) va-t-elle être à l'intérieur ou à l'extérieur de l'arc BB' ? Pour répondre à cette question, on doit calculer de combien avance la longitude de la Terre (ou du soleil apparent) par rapport au nœud de l'orbite lunaire durant une révolution synodique de la Lune (une lunaison). On a vu que la Terre (ou le soleil apparent) passe par le même nœud de l'orbite lunaire tous les 346,62 jours, donc la vitesse de la Terre par rapport à la ligne des nœuds est de 360°/346,64jours = 1,0386°/jour, or la révolution synodique moyenne de la Lune est de 29,53 jours, donc entre deux conjonctions consécutives la longitude de la Terre varie de 1,0386 x 29,53 = 30,67°.
Or cette valeur est inférieure à la valeur de l'arc qui est égale à 31,33°. Donc à chaque passage de la Terre (ou du soleil apparent) par un nœud de l'orbite lunaire il y a obligatoirement une éclipse de Soleil au voisinage de la conjonction dont la longitude est la plus proche du nœud de l'orbite lunaire.
Au moins deux éclipses (Lune et Soleil)
On peut donner une information supplémentaire, comme le critère en longitude est le même pour les éclipses de Lune, une demi-lunaison avant ou après la conjonction (nouvelle Lune) la Lune est en opposition (pleine Lune) et la Terre n'a parcouru que 15,335° en longitude par rapport au nœud, ces 15,335° correspondent à l'écart angulaire entre une conjonction et une opposition. Donc si une conjonction se trouve dans l'arc BB' l'opposition suivante ou l'opposition précédente se trouve obligatoirement aussi sur cet arc et il y a une éclipse de Lune, mais à l'autre nœud de l'orbite lunaire.
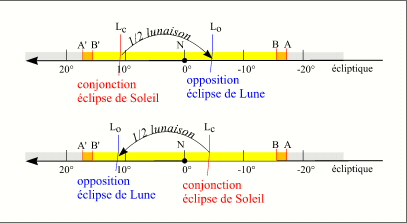
Conjonction et opposition au voisinage du nœud
Crédit : IMCCE/Patrick Rocher
À chaque saison d'éclipse, il y obligatoirement deux éclipses, une éclipse de Soleil et une éclipse de Lune.
Au plus trois éclipses (Lune et Soleil)
La variation de longitude de la Terre durant une lunaison étant de 30,67° et l'arc BB' ayant une longueur de 31,33°, il est également possible d'avoir deux conjonctions contenues dans l'arc BB'. Dans ce cas les conjonctions sont proches des extrémités de l'arc BB' et l'opposition comprise entre ces deux conjonctions est proche du nœud de l'orbite lunaire. De même on peut avoir deux oppositions dans l'arc BB'. Dans ce cas les oppositions sont proches des extrémités de l'arc BB' et la conjonction comprise entre ces deux oppositions se trouve proche du nœud de l'orbite lunaire. De plus comme nous l'avons déjà signalé, les éclipses proches des extrémités de l'arc BB' donc loin du nœud sont des éclipses faibles, donc des éclipses partielles de Soleil ou des éclipses de Lune par la pénombre et les éclipses proches du nœud sont des éclipses fortes, donc des éclipses centrales de Soleil ou des éclipses totales de Lune.
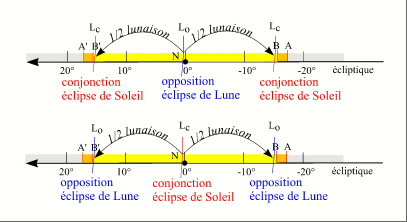
Conjonction et opposition au voisinage du nœud
Crédit : IMCCE/Patrick Rocher
On peut donc avoir une série de trois éclipses, au voisinage du passage de la Terre (ou du soleil apparent) par un nœud de l'orbite lunaire. Dans ce cas on a soit une éclipse forte de Soleil (éclipse centrale) encadrée par deux éclipses faibles de Lune (éclipses par la pénombre) ou une éclipse forte de Lune (éclipse totale) encadrée par deux éclipses faibles de Soleil (éclipses partielles).
Nombre d'éclipses par an
Une année civile du calendrier grégorien comporte 365 ou 366 jours. La lunaison moyenne est de 29,53 jours, une année lunaire de douze lunaisons a donc 354 jours, l'écart entre les deux années est de 11 ou 12 jours. Durant ces jours, la demi-lunaison étant supérieure à 14 jours, il ne peut pas y avoir à la fois une conjonction et une opposition. Donc une année civile ne peut jamais avoir à la fois 13 conjonctions (nouvelles Lunes) et 13 oppositions (pleines Lunes). Une seule de ces deux conjonctures est possible, dans ce cas la première conjonction ou opposition a lieu dans les 11 (ou 12) premiers jours de janvier et la dernière conjonction ou opposition a lieu dans les 11 (ou 12) derniers jours de décembre. On a donc, au maximum, soit une année civile à 13 oppositions, soit une année civile à 13 conjonctions. La saison des éclipses est égale à 173,31 jours, donc tous les 173 jours, aux conjonctions et oppositions les plus proches de ces dates il y a au moins deux éclipses (une de Soleil et une de Lune) et il y a au plus trois éclipses (deux de Lunes et une de Soleil ou deux de Soleil et une de Lune).
Une année civile peut contenir au maximum deux saisons d'éclipses entières, soit trois passages de la Terre par un des nœuds de l'orbite lunaire, le premier étant en début d'année, le second en milieu d'année et le dernier en fin d'année. À chacun de ces passages, on peut associer un couple ou un triplet d'éclipses. Mais l'on n'a jamais un triplet d'éclipses complet en début et en fin d'année, et dans le cas ou l'on a deux triplets complets à deux passages consécutifs le troisième passage ne comporte qu'une éclipse dans l'année en cours, car s'il présentait deux éclipses dans l'année en cours, il y aurait 13 oppositions et 13 conjonctions dans l'année, chose impossible. Donc dans une année civile, on a au maximum sept éclipses. Le tableau ci-dessous regroupe toutes les combinaisons possibles.
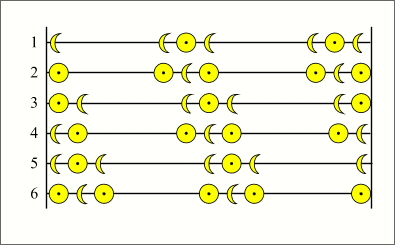
Liste des combinaisons possibles de 7 éclipses dans une année civile
Crédit : IMCCE/Patrick Rocher
On remarque dans ce tableau que les triplets d'éclipses qui se suivent à six lunaisons d'intervalle ont la même composition. En effet, comme on l'a déjà signalé, dans chaque triplet, l'éclipse médiane se produit très près du nœud, or l'éclipse médiane du triplet suivant sera forcement une éclipse du même corps, la conjonction ou l'opposition n'ayant avancé que de 4° environ. De plus lorsque l'on a sept éclipses par an la première et la dernière éclipses sont des éclipses du même corps, la première a toujours lieu dans les 11 (ou 12) premiers jours de janvier et la dernière a toujours lieu dans les 11 (ou 12) derniers jours de décembre.
En conclusion le nombre maximal d'éclipses dans une année civile est de sept éclipses, avec obligatoirement deux éclipses de Soleil et deux éclipses de Lune, pour les trois autres toutes les combinaisons sont possibles. Le nombre minimal d'éclipses dans une année est de quatre, avec obligatoirement deux éclipses de Lune et deux éclipses de Soleil.
Les séries courtes d'éclipses
Nous allons nous intéresser à l'évolution des éclipses au cours du temps. Supposons que nous ayons une éclipse de Lune à une date donnée comment sera l'éclipse suivante ?
Généralement les éclipses successives de Lune sont séparées par six lunaisons (liées à une saison d'éclipses), donc il y a alternance de nœud lunaire (nœud ascendant et nœud descendant). Nous avons vu que durant une lunaison la Terre (ou le Soleil apparent) progressait en moyenne de 30,67° en longitude par rapport à la ligne des nœuds de l'orbite lunaire, donc au bout de six lunaisons la Terre (ou le Soleil apparent) progresse de 6 x 30,67° = 184,02°, donc si dl1 est la différence de longitude entre l'opposition et le nœud de l'orbite lunaire pour la première éclipse, l'éclipse suivante a lieu au nœud suivant et la différence dl2 entre l'opposition et ce nœud est égale à dl1 - (184,02° - 180°) = dl1- 4,02°. Donc l'opposition se déplace par rapport aux nœuds successifs d'environ 4° dans le sens direct d'une éclipse à la suivante.
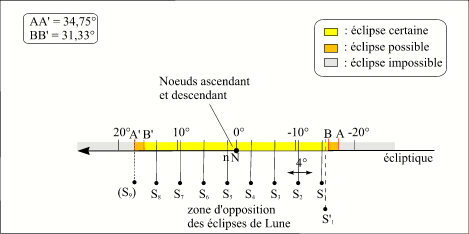
Série courte d'éclipse (vue depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Les éclipses de la suite courte S1 à S8 ont lieu à chaque saison d'éclipse, alternativement au nœud ascendant puis au nœud descendant. Il y a toujours au moins 8 éclipses dans la suite car l'arc BB' contient 7 arcs de 4° donc 8 éclipses. Il peut éventuellement y avoir une neuvième éclipse S9 (dans l'arc A'B'), dans ce cas cette éclipse est la dernière éclipse d'un triplet d'éclipses : Lune-Soleil-Lune. Dans ce cas l'opposition correspondant à la première éclipse du triplet a lieu une lunaison plus tôt et se trouve 30,67° en amont et cette éclipse est la première éclipse de la série courte suivante; nous avons donc un décrochage dans la suite des séries, la série suivante commence avant que la série en cours ne soit terminée. Ce phénomène peut également se produire lorsque la huitième éclipse de la série est très proche du point B'. On peut donc conclure que les éclipses des suites courtes sont séparées par six lunaisons et que la première éclipse d'une suite courte est séparée de la dernière éclipse de suite courte précédente par cinq lunaisons ou par une lunaison (antérieure) dans le cas d'un décrochage.
On remarque que les oppositions liées aux éclipses d'une série courte parcourent l'arc BB' dans le sens direct avec un pas moyen de 4°, les premières et les dernières éclipses sont des éclipses faibles (éclipses par la pénombre) et les éclipses du milieu de la série, proches des nœuds, sont des éclipses fortes (éclipses partielles par l'ombre, puis éclipses totales).
Attention, il ne faut jamais oublier que ces calculs sont faits à l'aide des révolutions moyennes de la Lune, la réalité est toujours un peu différente, l'avance de l'opposition n'est jamais exactement égale à 4° mais varie autour de cette valeur moyenne.
Répartition des éclipses sur une période de 22 ans
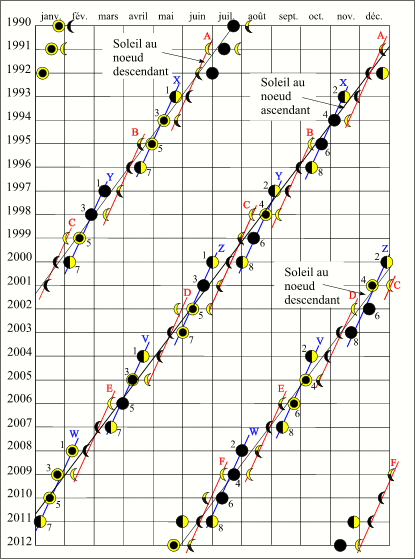
Éclipses de Lune et de Soleil entre 1990 et 2012.
Crédit : IMCCE/Patrick Rocher
Sur le diagramme ci-dessus nous avons fait figurer l'ensemble des éclipses de Lune et de Soleil comprises entre l'an 1990 et l'an 2012. Les éclipses sur ce diagramme sont représentées de la manière suivante :

Crédit : IMCCE/Patrick Rocher
On remarque que les éclipses ont bien lieu aux voisinages des passages du Soleil dans la direction des nœuds ascendant et descendant de l'orbite lunaire. Sur ce dessin nous avons signalé la nature des noeuds (ascendant ou descendant) relative au éclipses de Soleil. De même on constate qu'à chaque saison d'éclipse on a un doublet d'éclipses Lune-Soleil ou un triplet d'éclipses Lune-Soleil-Lune (1991) ou Soleil-Lune-Soleil (2000) et que dans le cas des triplets les éclipses en première et dernière positions sont faibles et que l'éclipse médiane est forte. On observe que les éclipses de Soleil ou de Lune de début et de fin de séries courtes sont séparées par cinq ou une lunaisons. On vérifie également qu'il y a toujours au moins quatre éclipses par an, sur la période de temps représentée, il n'y a pas d'année à 7 éclipses, mais une année à 6 éclipses (2000).
La démonstration de l'existence des séries courtes de Soleil est également valable pour des séries courtes d'éclipses de Lune. Il suffit de remplacer la conjonction par l'opposition. Sur notre diagramme nous avons fait figurer les séries courtes de Soleil (en bleu) et les séries courtes de Lune (en rouge). On constate que les traits joignant les éclipses d'une même série pour chaque nœud sont parallèles et coupent les lignes des nœuds. Sur la période considérée, il n'y a pas de série courte à 9 éclipses. Mais on peut observer plusieurs décrochage de séries courtes, par exemple la série courte de Soleil Z débute avant que la série Y soit terminée (triplet d'éclipses de l'an 2000).
Canons et grandeurs des éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section nous étudions la grandeur des éclipses de Lune. Qu'elles sont les éclipses les éclipses les plus longues et les éclipses les plus grandes en fonction des positions de la Lune par rapport au périgée et à l'apogée de son orbite et par rapport au position de la Terre sur son orbite.
Grandeurs des éclipses de Lune
Nous avons vu que la taille des cônes d'ombre et de pénombre dépend de deux paramètres, la distance Soleil-Terre qui conditionne la position des sommets des cônes et la distance Terre-Lune qui conditionne la position du plan d'intersection des cônes.
Les éclipses les plus longues seront des éclipses centrales, la durée de l'éclipse est fonction de la vitesse synodique de la Lune, c'est à dire de la différence des vitesses entre la Lune et les cônes d'ombre et de pénombre car la Lune et les cônes d'ombre et de pénombre se déplacent dans le même sens par rapport à la Terre (sens direct). Le tableau suivant donne les valeurs extrêmes du demi-diamètre apparent (ρ) du cône d'ombre en tenant compte des corrections de réfraction. Pour ces valeurs on donne également les positions de la Terre et de la Lune, la valeur du demi-diamètre apparent de la pénombre (σ), la vitesse synodique de la Lune en secondes de degré par heure, la grandeur de l'éclipse et la durée totale de l'éclipse.
Demi-diamètre de l'ombre 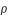
|
Minimal : 2,61sL
|
Moyen : 2,69 sL
|
Maximal 2,78 sL
|
| Positions de la Lune et de la Terre |
Lune apogée - Terre périhélie |
--- |
Lune périgée - Terre aphélie |
Demi-diamètre de la pénombre 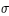
|
4253" = 4,82 sL
|
4425" = 4,75 sL
|
4678" = 4,65 sL
|
| Vitesse synodique de la Lune |
1626"/h |
1858"/h |
2150"/h |
| Grandeur de l'éclipse |
1,805 |
1,845 |
1,890 |
| Durée de l'éclipse |
environ 6h 19m |
environ 5h 46m |
environ 5h 17m |
La grandeur maximale s'observe dans le cas des éclipses centrales périgées (avec la Terre à l'aphélie), mais la durée maximale s'observe pour les éclipses apogées (avec la Terre au périhélie) ; en effet dans ce cas le diamètre apparent de la Lune est plus petit mais son mouvement synodique est plus lent. On retrouve donc la dualité déjà observée dans le cas des éclipses de Soleil de durée maximale (éclipses annulaires à l'apogée) et les éclipses de Soleil de grandeur maximale (éclipses totales au périgée).
Les canons d'éclipses de Lune
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement par Dover Publications. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses de Lune de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Soleil comprises entre -2002 et +2526.
À l'IMCCE, nous avons construit un canon d'éclipses de Lune et de Soleil. Il porte sur une période de 6000 ans (de l'an -2999 à 3000), il a été construit avec les dernières théories planétaires et lunaire élaborées à l'IMCCE.
Ces trois canons ont été construits avec des théories différentes des corps célestes et avec des constantes légèrement différentes, cela implique que certaines éclipses limites ne sont pas identiques (apparition ou disparition d'éclipses limites par la pénombre, ou éclipses totales dans un canon qui deviennent partielles dans l'autre).
En savoir plus: Le canon de l'IMCCE
 En savoir plus: Le canon d'éclipses de Lune de l'IMCCE
En savoir plus: Le canon d'éclipses de Lune de l'IMCCE
Les théories utilisées
Pour construire notre canon nous avons utilisé les théories suivantes :
- Théorie de la Lune : ELP2000 de Michèle Chapront-Touzé et J. Chapront.
- Théorie du barycentre Terre-Lune : VSOP82 de P. Bretagnon.
- Éphémérides sous forme de polynômes de Tchebycheff : SLP98 de G. Francou
- TT-TU : valeurs de R. Stephenson (1984) modifiées et adaptées à la théorie de la Lune utilisée.
- Théorie de la précession de Lieske (1977).
- Théorie de la nutation de Wahr (1981).
- Temps sidéral d'Aoki (1992)
Les paramètres physiques
Les paramètres physiques utilisés sont les suivants :
- le demi-diamètre solaire = 15' 59.63".
- le rapport du rayon lunaire sur le rayon équatorial terrestre : k = 0,2725076.
- le rayon équatorial terrestre = 6378140m.
- On tient compte de la réfraction atmosphérique en augmentant le demi-diamètre géocentrique apparent de l'ombre de 1/73 et en augmentant le demi-diamètre géocentrique apparent de la pénombre de 1/128.
Les résultats
Nous avons trouvé sur cette période de 6000 ans, 14357 éclipses de Lune qui se répartissent de la manière suivante :
- Nombre d'éclipses totales : 4210 (soit 29,3% des éclipses).
- Nombre d'éclipses partielles : 5019. (soit 34,9% des éclipses)
- Nombre d'éclipses par la pénombre : 5128 ( soit 35,7%) dont 164 totales par la pénombre.
Comme on l'a prédit précédemment, on vérifie que la proportion d'éclipses par l'ombre est bien d'environ 64% et la proportion d'éclipses par la pénombre est bien d'environ 36%.
Les éclipses totales les plus longues
Comme nous venons de le voir, il n'y a pas coïncidence entre les éclipses totales les plus grandes et les éclipses totales les plus longues. Les éclipses les plus longues ont lieu avec une Lune proche de l'apogée.
Le tableau suivant donne les 21 éclipses du canon de l'IMCCE dont la durée de la phase totale est supérieure à 1h46m. On remarquera que la valeur maximale de la grandeur de ces éclipses est de 1.8176336.
| Date de l'éclipse |
Magnitude |
Durée de la phase totale |
| 29/06-2344-30/06/-2344 |
1.7559958 |
01h46m05s |
| 01/06-2203 |
1.7995766 |
01h46m37s |
| 04/05/-2062 |
1.7921950 |
01h46m36s |
| 06/04-1921 |
1.8050155 |
01h46m27s |
| 23/06/-1646 - 24/06/-1646 |
1.7914130 |
01h46m16s |
| 26/05/-1505 |
1.7992139 |
01h46m30s |
| 27/04/-1364 |
1.8054797 |
01h46m29s |
| 30/03/-1223 |
1.8010124 |
01h46m15s |
| 16/07/-503 |
1.7999741 |
01h46m04s |
| 11/04/-98 |
1.8002998 |
01h46m02s |
| 07/08/54 |
1.8104677 |
01h46m13s |
| 28/06/177 |
1.7716335 |
01h46m23s |
| 31/05/318 |
1.7820179 |
01h46m33s |
| 03/05/459 |
1.8176336 |
01h46m33s |
| 12/06/1443 |
1.8083912 |
01h46m15s |
| 24/05/1584 |
1.8152958 |
01h46m06s |
| 13/08/1859 |
1.8150878 |
01h46m28s |
| 16/07/2000 |
1.7686611 |
01h46m25s |
| 09/06/2123 |
1.7489899 |
01h46m07s |
| 19/06/2141 |
1.7416402 |
01h46m07s |
| 11/05/2264-12/05/2264 |
1.7985597 |
01h46m14s |
Parmi cette liste, chaque éclipse appartient à un triplet d'éclipses et est encadrée par deux éclipses partielles de Soleil. En effet l'opposition étant toujours proche du noeud donc du milieu de l'intervalle BB', la conjonction précédente et la conjonction suivante tombent également à l'intérieur de l'intervalle, on a donc toujours un triplet d'éclipses. Par exemple l'éclipse du 01/06/-2203 qui a la plus longue phase totale et qui a duré au total 6h 14m 10s, est encadrée par les éclipses partielles de Soleil du 18/05/-2203 et de 16/06/-2203.
Pour cette éclipse on peut vérifier que c'est bien une éclipse apogée avec une opposition proche du passage au nœud de l'orbite :
- le 01/06/-2203 à 19h 02m 46s UT : la Lune passe par le nœud descendant de son orbite.
- e 01/06/-2203 à 19h 09m 59s UT : maximum de l'éclipse de Lune.
- le 01/06/-2203 à 19h 10m 11s UT : Pleine Lune.
- le 03/06/-2203 à 01h 26m 53s UT : la Lune à l'apogée d=406185 km, diam. app. =29.5'.
On vérifie que conformément à ce que nous avons dit lors de la définition du critère en latitude, le maximum de l'éclipse a lieu entre l'instant du passage au nœud et l'instant de la pleine Lune lorsque le passage au nœud est antérieur à la pleine Lune.
Les éclipses totales les plus grandes
Les éclipses totales les plus grandes correspondent à des éclipses totales périgées. Le tableau ci-dessous nous donne les 26 éclipses totales de Lune du canon de l'IMCCE dont la grandeur est supérieure à 1,86.
| Date des éclipses |
Grandeur |
Durée de la phase totale |
| 08/07/-2977 |
1.8775476 |
01h39m15s |
| 29/07/-2420 |
1.8647245 |
01h40m04s |
| 15/01/-2326 |
1.8620205 |
01h38m35s |
| 27/03/-1874 |
1.8748617 |
01h40m19s |
| 16/02/-1751 |
1.8621251 |
01h39m52s |
| 04/06/-1552 |
1.8753223 |
01h40m19s |
| 07/05/-1411 |
1.8661648 |
01h40m22s |
| 09/04/-1270 |
1.8725565 |
01h40m16s |
| 12/09/-1241 - 13/09/-1241 |
1.8672238 |
01h38m32s |
| 28/02/-1147 - 01/03/-1147 |
1.8730227 |
01h39m45s |
| 24/07/-1136 |
1.8776169 |
01h39m10s |
| 29/12/-540 |
1.8636202 |
01h38m10s |
| 09/01/-521 -10/01/-521 |
1.8684891 |
01h38m15s |
| 01/04/-51 |
1.8634609 |
01h39m44s |
| 10/02//54 - 11/02/54 |
1.8693552 |
01h39m16s |
| 17/07/83 |
1.8618347 |
01h41m49s |
| 06/09/564 |
1.8743438 |
01h38m54s |
| 30/07/687 |
1.8620946 |
01h39m18s |
| 24/04/1092 |
1.8737558 |
01h39m20s |
| 28/09/1121 |
1.8682270 |
01h38m55s |
| 09/08/1226 |
1.8794485 |
01h39m39s |
| 15/05/1631 |
1.8728523 |
01h39m48s |
| 30/08/1765 |
1.8631087 |
01h41m28s |
| 26/07/1953 |
1.8628642 |
01h40m44s |
| 04/11/2264 - 05/11/2264 |
1.8688193 |
01h38m37s |
| 05/06/2756 |
1.8799400 |
01h39m20s |
Chaque éclipse de Lune de cette liste appartient à un triplet d'éclipses et est encadrée par deux éclipses partielles de Soleil. Par exemple, l'éclipse du 05/06/2756 qui est la plus grande, dont la durée totale est de 5h 17m 31s, est encadrée par les éclipses partielles de Soleil du 21/05/2756 et du 19/06/2756.
Pour cette éclipse on peut vérifier que c'est bien une éclipse périgée avec une opposition proche du passage au nœud de l'orbite :
- le 05/06/2756 à 03h 38m 22s UT : la Lune passe par le nœud ascendant de son orbite.
- le 05/06/2756 à 03h 41m 34s UT : maximum de l'éclipse de Lune.
- le 05/06/2756 à 03h 41m 40s UT : Pleine Lune.
- le 05/06/2756 à 09h 01m 51s UT : la Lune au périgée d=357129 km, diam. app. =33.5'.
On vérifie de nouveau que le maximum de l'éclipse a lieu entre le passage au nœud et la pleine Lune.
Les éclipses les plus faibles et les plus courtes
Contrairement au cas des éclipses totales de Lune de grandeur maximale et des éclipses totales de Lune de durée maximale, il y a coïncidence entre les éclipses de Lune les plus courtes et les éclipses de grandeur minimale. Il s'agit d'éclipses rasantes par l'ombre dans le cas des éclipses partielles et par la pénombre dans le cas des éclipses par la pénombre. Le tableau ci-dessous nous donne les 6 éclipses partielles de Lune du canon de l'IMCCE dont la grandeur est inférieure à 0,001.
| Date de l'éclipse |
Grandeur |
Durée de la phase partielle |
| 14/09/-2237 |
0.0009512 |
7m36s |
| 08/08/-1463 |
0.0002822 |
3m39s |
| 02/07/-754 |
0.0004297 |
4m47s |
| 13/10/273 |
0.0000806 |
1m58s |
| 24/022157 |
0.0004892 |
5m27s |
| 16/06/2421 |
0.0006280 |
5m34s |
Le tableau ci-dessous nous donne les 2 éclipses de Lune par la pénombre du canon de l'IMCCE dont la grandeur est inférieure à 0,001.
| Date de l'éclipse |
Grandeur |
Durée de l'éclipse |
| 07/07/1571 |
0.0004848 |
5m53s |
| 17/01/2986 |
0.0006936 |
8m01s |
Ces deux dernières éclipses de Lune appartiennent à des triplets d'éclipses. Ainsi l'éclipse du 07/07/1571 est la première du triplet comprenant ensuite l'éclipse annulaire de Soleil des 21 et 22/07/1571 puis l'éclipse partielle de Lune du 05/08/1571. De même l'éclipse du 17/01/2986 est la première du triplet comprenant ensuite l'éclipse annulaire-totale de Soleil du 31/01/2986 puis l'éclipse de Lune par la pénombre du 15/02/2986.
Il convient de remarquer que ces éclipses sont des cas limites propres au canon de l'IMCCE, les cas limites des autres canons d'éclipses de Lune sont différents, les constantes et les éphémérides utilisées pour l'élaboration des canons étant différentes.
Le Saros et les suites longues d'éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section, nous reprenons la notion de Saros et du nombre moyen d'éclipses de Lune dans un Saros. Nous étudions l'évolution des éclipses dans les séries longues d'éclipses homogènes et nous donnons un exemple de série longue d'éclipses.
Nombre d'éclipses dans un Saros
Le définition du saros et les démonstrations qui lui sont liées ont été traitées dans la partie relative aux éclipses de Soleil. Nous redonnons ici que les particularités propres aux nombres d'éclipses.
Le saros comporte 38 saisons d'éclipses, revenant en moyenne toutes les 5 ou 6 lunaisons. À chaque saison d'éclipses il y a au moins deux éclipses et parfois trois éclipses. En moyenne un saros comprend 84 éclipses, réparties en 42 éclipses de Soleil et 42 éclipses de Lune.
Les 42 éclipses de Lune se répartissent de la manière suivante : 14 éclipses par la pénombre, 28 éclipses par l'ombre dont 14 éclipses partielles et 14 éclipses totales.
Les 42 éclipses de Soleil se répartissent de la manière suivante : 14 éclipses partielles et 28 éclipses centrales.
Ce nombre d'éclipses par saros est une valeur moyenne, en réalité il existe des saros riches pouvant atteindre jusqu'à 94 éclipses (47 de chaque) et des saros pauvres comportant 78 éclipses.
Les canons d'éclipses construits à l'IMCCE comportent 28512 éclipses sur une période de 5999 ans, soit en moyenne 4,7528 éclipses par an et 85,7 éclipses par saros (valeur que l'on peut arrondir à 86). Cette valeur est légèrement plus forte que la valeur moyenne (84). On retrouve le saros moyen du canon d'Oppolzer, construit sur une période plus courte, qui est de 86 éclipses.
Eclipses homologues et suites longues d'éclipses de Lune
Nous avons vu qu'il existe une période de récurrence des éclipses, le saros, qui ramène sensiblement la même éclipse après une période de 6585,32 jours. Ces éclipses séparées par un saros sont appelées éclipses homologues. En réalité, elles ne sont pas parfaitement identiques, mais elles évoluent légèrement d'un saros à l'autre et elles forment des suites qui portent sur de grandes périodes de temps d'où leur nom de suites longues.
Evolution de la longitude de l'opposition après un saros
Nous allons regarder comment évolue la longitude de l'opposition après une période d'un saros. L'écart entre le saros de 223 lunaisons « L » et les 242 révolutions draconitiques « G » est de moins 52 minutes de temps (- 0,03612 jour).
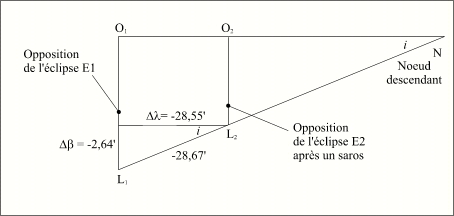
Variation de la longitude de l'opposition entre deux éclipses homogènes
Crédit : IMCCE/Patrick Rocher
Durant ces 52 minutes la Lune, sur son orbite, se déplace en moyenne par rapport à son nœud de -0,03612 x 360°/G = -28,67'. La Lune en opposition se trouve donc déplacée sur son orbite de 28,67' dans le sens rétrograde par rapport au nœud. Compte tenu de l'inclinaison de l'orbite lunaire, ce décalage se traduit par un décalage de la longitude céleste Δλ = -28,55' et par une variation de la latitude céleste de la Lune de Δβ = -2,64'.
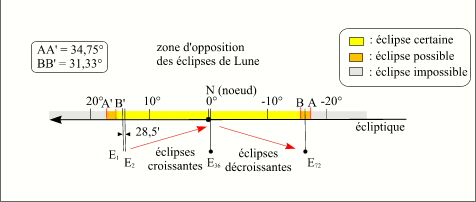
Évolution sur une suite longue d'éclipses
Crédit : IMCCE/Patrick Rocher
Les oppositions des éclipses homologues vont donc parcourir l'arc BB' dans le sens rétrograde avec un pas moyen de 28,55'. Si l'on divise l'arc BB' par 28,55', on constate qu'il peut contenir 66 éclipses et si l'on divise l'arc AA' par 28,55' on voit qu'il peut contenir 74 éclipses. Ces suites d'éclipses sont appelées suites longues. L'étude des canons d'éclipses montre qu'en moyenne ces suites comportent 72 éclipses. Ce qui correspond à une période de temps d'environ 1300 ans.
Aspect d'une suite longue d'éclipse de Lune
Les premières éclipses d'une suite longue sont faibles, car elles sont proches de l'arc A'B', donc loin du nœud. Ensuite, leur grandeur va croître jusqu'à ce qu'elles se produisent au voisinage du nœud, puis leur grandeur va décroître pour finir de nouveau faible au voisinage de l'arc BA. Pour une suite longue de 72 éclipses, si l'on respecte les pourcentages des différents types d'éclipses (environ 1/3 de chaque), on aura donc successivement 12 éclipses par la pénombre de grandeur croissante, puis 12 éclipses partielles par l'ombre, puis 12 éclipses totales de grandeur croissante (sur 650 ans), puis de nouveau 12 éclipses totales de grandeur décroissante, puis 12 éclipses partielles par l'ombre et enfin 12 éclipses par la pénombre de grandeur décroissante (sur 650 ans). Dans la pratique, les deux ou trois éclipses du milieu de la suite longue sont maximales, elles servent de transition entre la période de croissance et de décroissance des éclipses totales. On remarque que toutes les éclipses d'une suite ont lieu au même nœud. Si la suite longue a lieu au nœud descendant les latitudes célestes successives de la Lune croissent des latitudes négatives aux latitudes positives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du sud au nord. Inversement pour une suite longue au nœud ascendant les latitudes célestes successives de la Lune décroissent des latitudes positives aux latitudes négatives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du nord au sud. En réalité, dans les propos précédents, les directions nord et sud désignent le nord et le sud par rapport à l'écliptique et non par rapport à l'équateur terrestre, il faut bien se rappeler que l'écliptique est incliné par rapport à l'équateur terrestre.
Evolutions des éclipses homologues
Evolution en longitude terrestre
Nous avons vu que la période du saros n'est pas un nombre entier de jours, sa valeur est de 6585,32 jours. Donc entre deux éclipses homologues, la Terre n'a pas tourné d'un nombre entier de jour, les zones concernées par les éclipses ne sont donc pas les mêmes. En 0,32 jour, la Terre tourne d'environ 120°, les zones concernées par l'éclipse se déplacent donc d'environ 120° vers l'ouest. Comme une éclipse de Lune est visible, au moins durant une partie de sa durée, sur environ les deux tiers de la surface terrestre, il n'est pas surprenant que des éclipses homologues successives soient visibles d'un même lieu. Après trois saros, l'éclipse a même lieu sensiblement au même instant. Cela explique que la période de récurrence des éclipses (saros) soit plus facilement décelable, en un lieu, à travers les suites d'éclipses de Lune observées. Ce qui n'est pas le cas pour les éclipses de Soleil.
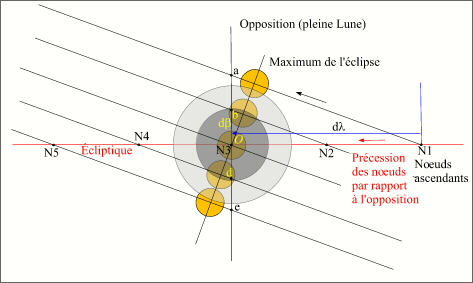
Évolution en latitude
Crédit : IMCCE/Patrick Rocher
Evolution en latitude écliptique par rapport aux cônes d'ombre et de pénombre
Le dessin ci-dessus nous montre l'évolution des éclipses homogènes de Lune durant une suite longue de saros au nœud ascendant. Sur cette figure nous avons figée la longitude de la pleine Lune (opposition), ce sont donc les positions du nœud ascendant qui vont variées dans le sens direct par rapport à l'opposition au cours du temps. Nous avons représenté la position du nœud ascendant environ tous les 325 ans ainsi que les maxima des éclipses correspondantes c'est-à-dire les distances minimales entre le centre de la Lune et le centre des cônes.
Au début de la suite longue d'éclipse de Lune, le nœud se trouve en position N1, à l'ouest de l'opposition, la Lune va donc passer d'ouest en est devant le bord nord du cône de pénombre, les premières éclipses de la suite seront donc des éclipses par la pénombre passant au bord nord de la pénombre (éclipsant donc le sud de la Lune). 325 ans plus tard, le nœud ascendant de l'orbite lunaire est en N2, la Lune rencontre le bord nord du cône d'ombre, les éclipses de Lune sont donc partielles par l'ombre. 325 ans plus tard, le nœud ascendant N3 est confondu avec la longitude de l'opposition, c'est le cas idéal d'une éclipse totale centrale, puis nous avons une situation symétrique par rapport à l'opposition, c'est-à-dire un nœud en N4 correspondant à des éclipses partielles par l'ombre mais au sud du cône d'ombre (éclipsant le nord de la Lune), puis des éclipses par la pénombre au sud du cône de pénombre qui prennent fin après la dernière position N5 du nœud.
On remarque que lorsque le nœud ascendant est à l'ouest de l'opposition le maximum de l'éclipse a lieu avant l'opposition, et que lorsque le nœud ascendant est à l'est de l'opposition le maximum de l'éclipse a lieu après l'opposition. Donc la connaissance de l'instant du maximum de l'éclipse, de l'instant de l'opposition et de la nature du nœud (ascendant ou descendant) permet de situer la position de l'éclipse dans la suite longue d'éclipses homogènes et la partie de la Lune éclipsée. Ou bien, inversement , la connaissance de la position d'une éclipse dans sa suite longue et la nature du nœud permet de savoir si le maximum de l'éclipse a lieu avant ou après l'opposition et de connaître la partie de la Lune éclipsée.
En savoir plus: Positions des éclipses d'une saison éclipse
 En savoir plus
En savoir plus
Positions des éclipses d'une saison dans les suites longues de saros
Nous avons vu qu'à chaque saison d'éclipse il y a soit un doublet soit un triplet d'éclipses de Lune et de Soleil. Nous allons essayer de déterminer les positions des éclipses de Lune et de Soleil dans leurs suites longues respectives en fonction de l'allure du triplet ou du doublet d'éclipses. On rappelle que lors d'une saison d'éclipse il y a inversion des nœuds avec la nature des éclipses, ainsi si l'éclipse ou les éclipses de Soleil ont lieu au nœud ascendant l'éclipse ou les éclipses de Lune de la même saison ont lieu au nœud descendant et inversement.
Cas d'un doublet d'éclipses
Dans le cas d'un doublet d'éclipses, l'opposition et la conjonction (les syzygies) sont toujours réparties de part et d'autre des nœuds. Donc l'éclipse correspondant à la syzygie à l'ouest (à droite) du nœud est dans la partie décroissante de sa suite longue et l'éclipse correspondant à la syzygie à l'est (à gauche) du nœud suivant est dans la partie croissante de sa suite longue.
 Exemple
Exemple
Soit un doublet constitué d'une éclipse de Lune au nœud descendant suivie d'une éclipse de Soleil au nœud ascendant. Comme l'éclipse de Lune a lieu avant le passage au nœud, l'opposition est à l'ouest du nœud et l'éclipse de Lune est dans la partie décroissante de sa suite longue (au nœud descendant) et c'est donc la partie sud du disque lunaire qui est éclipsée. L'éclipse de Soleil, elle, a lieu après le passage au nœud, la conjonction est donc à l'est du nœud et l'éclipse de Soleil est dans la partie croissante de sa suite longue (au nœud ascendant), elle sera donc visible dans l'hémisphère nord.
Le tableau ci-dessous résume tous les cas possibles pour un doublet d'éclipses
| Ordre du doublet |
Eclipse de Lune - Eclipse de Soleil |
Eclipse de Soleil - Eclipse de Lune |
| Position de l'éclipse de Lune dans sa suite longue |
partie déroissante |
partie croissante |
| Position de l'éclipse de Soleil dans sa suite longue |
partie croissante |
partie décroissante |
| Eclipse Lune au noeud descendant
Eclipse de Soleil au noeud ascendant |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
| Eclipse Lune au noeud ascendant
Eclipse Soleil au noeud descendant |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
Cas d'un triplet d'éclipses
Dans le cas d'un triplet d'éclipses, la première et la troisième éclipses sont de même nature (éclipses de Lune ou éclipses de Soleil) et la seconde éclipse est de nature opposée aux deux autres. La première éclipse appartient à la partie décroissante de sa suite longue et est proche de la fin de cette suite. La troisième appartient à la partie croissante de sa suite longue et est proche du début de cette suite. Pour l'éclipse du milieu, elle est proche du maximum dans sa suite longue, on peut la situer dans la partie croissante ou décroissante de sa suite, uniquement si l'on connaît la position de la syzygie par rapport au nœud, une syzygie à l'ouest du nœud la place dans la partie décroissante et une syzygie à l'est du nœud la place dans la partie croissante de sa suite.
 Remarque
Remarque
Dans les explications ci-dessus, la position à l'ouest (à droite) du nœud est équivalente à une syzygie antérieure au passage au nœud et une position à l'est (à gauche) est équivalente à une syzygie postérieure au passage au nœud. De même nous avons basé nos explications sur les positions relatives des nœuds et des syzygies, nous aurions pu faire les mêmes raisonnements en remplaçant un des deux éléments par la position, ou l'instant, du maximum des éclipses.
Evolutions des suites homologues - suite
Variation sur le fond d'étoile et dans l'année
Nous rappelons que d'un saros à l'autre, le Soleil, donc l'éclipse se décale d'environ 10,5° par rapport aux constellations zodiacales. Au cours d'une suite longue le soleil apparent effectue plus de deux tours complets d'orbite et l'on rencontre toutes les configurations liées au soleil apparent. Les éclipses parcourent les quatre saisons et cela deux fois.
Variation des types d'éclipses
Nous avons vu également que suite à l'écart entre un saros et 239 révolutions anomalistiques, la distance de la Lune à son périgée varie de 2,8° d'un saros à l'autre. Au cours d'une suite longue de 72 saros, les conjonctions lunaires liées aux éclipses homologues (donc la Lune) ne vont parcourir que 202° de l'orbite lunaire, soit un peu plus que la moitié. De plus durant les 48 éclipses centrales du saros, cet arc se réduit à 134°, il convient de comparer cette valeur avec les portions de l'orbite lunaire où les éclipses sont totales ou annulaires.
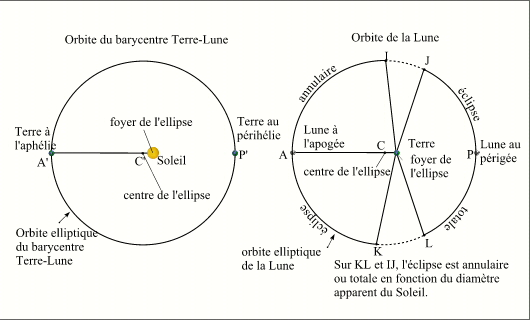
Orbites de la Terre et de la Lune
Crédit : IMCCE/Patrick Rocher
Ainsi si le périgée est proche du milieu de cet arc de 134°, la suite longue est riche en éclipses totales, si au contraire, cet arc avoisine l'apogée la suite longue est riche en éclipses annulaires.
 Remarque
Remarque
Il ne faut jamais perdre de vu que toutes les variations dans les suites longues sont calculées avec des valeurs moyennes et ne sont jamais tout à fait conformes à la réalité. Ainsi le décalage de la conjonction par rapport au nœud de 28,55' est une valeur moyenne. En réalité le Soleil avance plus vite en janvier (il est proche du périgée) qu'en juillet (proche de l'apogée), le calcul montre que la variation de la longitude de la conjonction par rapport au nœud est de l'ordre de 6' en janvier (au lieu de 28,55') et qu'elle atteint 48' en juillet. Les éclipses homologues d'hiver sont donc plus semblables que les éclipses homologues d'été qui évoluent sensiblement plus vite.
Il est facile de connaître la position d'une éclipse dans une suite longue d'éclipses. Les éclipses croissantes ont toujours lieu après le passage au nœud et les éclipses décroissantes ont toujours lieu avant le passage au nœud. La connaissance des instants des syzygies et du passage au nœud permet donc de positionner l'éclipse dans sa suite longue. Inversement la connaissance de la position d'une éclipse dans sa suite longue permet, sauf pour l'éclipse maximale, de savoir sa position par rapport aux nœuds. De plus dans le cas d'un doublet d'éclipses (Lune Soleil ou Soleil Lune) la première éclipse, qui a lieu avant le passage au nœud appartient à la partie décroissante de sa suite longue et la seconde éclipse appartient à la partie croissante de sa suite longue. Dans le cas d'un triplet d'éclipses, la première appartient à la fin de la partie décroissante de la suite longue qui la contient, la dernière appartient au début de la partie croissante de la suite longue qui la contient et l'éclipse médiane se trouve au voisinage du maximum de sa suite longue.
En savoir plus: Exemple de Saros
 En savoir plus
En savoir plus
Exemple de suite longue
Le tableau suivant donne la liste des éclipses de la suite longue contenant l'éclipse du 31 mai 2003. On donne successivement le numéro de l'éclipse dans la suite longue, le type d'éclipse, la date de l'éclipse, sa magnitude et la durée maximale de la phase centrale lorsque cette phase existe.
| N° |
type |
date |
magnitude |
durée |
| 1 |
P |
12/10/1624 |
0.0085968 |
|
| 2 |
P |
23/10/1642 |
0.0548679 |
|
| 3 |
P |
03/11/1660 |
0.0896182 |
|
| 4 |
P |
14/11/1678 |
0.1146153 |
|
| 5 |
P |
24/11/1696 |
0.1316624 |
|
| 6 |
P |
07/12/1714 |
0.1419092 |
|
| 7 |
P |
17/12/1732 |
0.1469513 |
|
| 8 |
P |
28/12/1750 |
0.1505860 |
|
| 9 |
P |
08/01/1769 |
0.1530883 |
|
| 10 |
P |
19/01/1787 |
0.1591577 |
|
| 11 |
P |
30/01/1805 |
0.1675941 |
|
| 12 |
P |
11/02/1823 |
0.1857746 |
|
| 13 |
P |
21/02/1841 |
0.2097100 |
|
| 14 |
P |
04/03/1859 |
0.2462690 |
|
| 15 |
P |
15/03/1877 |
0.2919636 |
|
| 16 |
P |
26/03/1895 |
0.3533467 |
|
| 17 |
P |
06/04/1913 |
0.4246662 |
|
| 18 |
P |
17/04/1931 - 18/04/1931 |
0.5110283 |
|
| 19 |
P |
28/04/1949 |
0.6095708 |
|
| 20 |
P |
09/05/1967 |
0.7205292 |
|
| 21 |
P |
19/05/1985 |
0.8411277 |
|
| 22 |
A |
31/05/2003 |
0.9696001 |
03m34.08s |
| 23 |
A |
10/06/2021 |
0.9721316 |
03m47.99s |
| 24 |
A |
21/06/2039 |
0.9730915 |
04m01.45s |
| 25 |
A |
01/07/2057 - 02/07/2057 |
0.9735738 |
04m18.67s |
| 26 |
A |
13/07/2075 |
0.9737206 |
04m40.41s |
| 27 |
A |
23/07/2093 |
0.9737206 |
05m06.77s |
| 28 |
A |
04/08/2111 |
0.9731384 |
05m36.78s |
| 29 |
A |
14/08/2129 - 15/08/2129 |
0.9724857 |
06m09.32s |
| 30 |
A |
26/08/2147 |
0.9716470 |
06m42.98s |
| 31 |
A |
05/09/2165 |
0.9706588 |
07m15.78s |
| 32 |
A |
16/09/2183 - 17/09/2183 |
0.9695596 |
07m46.87s |
| 33 |
A |
28/09/2201 |
0.9684309 |
08m14.61s |
| 34 |
A |
09/10/2219 |
0.9672517 |
08m39.72s |
| 35 |
A |
19/10/2237 |
0.9661547 |
09m00.30s |
| 36 |
A |
30/10/2255 - 31/10/2255 |
0.9651065 |
09m17.21s |
| 37 |
A |
10/11/2273 |
0.9642541 |
09m28.20s |
| 38 |
A |
21/11/2291 |
0.9635287 |
09m34.68s |
| 39 |
A |
02/12/2309 - 03/12/2309 |
0.9630803 |
09m34.31s |
| 40 |
A |
14/12/2327 |
0.9628599 |
09m28.43s |
| 41 |
A |
24/12/2345 |
0.9629606 |
09m15.58s |
| 42 |
A |
04/01/2364 - 05/01/2364 |
0.9633421 |
08m57.77s |
| 43 |
A |
15/01/2382 |
09640683 |
08m34.41s |
| 44 |
A |
26/01/2400 |
0.9651082 |
08m07.46s |
| 45 |
A |
05/02/2418 - 06/02/2418 |
0.9664621 |
07m37.67s |
| 46 |
A |
17/02/2436 |
0.9681073 |
07m06.45s |
| 47 |
A |
27/02/2454 |
0.9700297 |
06m34.42s |
| 48 |
A |
09/03/2472 - 10/03/2472 |
0.9721718 |
06m02.57s |
| 49 |
A |
21/03/2490 |
0.9745093 |
05m31.07s |
| 50 |
A |
01/04/2508 |
0.9769654 |
05m00.43s |
| 51 |
A |
12/04/2526 - 13/04/2526 |
0.9795505 |
04m29.66s |
| 52 |
A |
23/04/2544 |
0.9821258 |
03m59.66s |
| 53 |
A |
04/05/2562 |
0.9847154 |
03m29.01s |
| 54 |
A |
14/05/2580 -15/05/2580 |
0.9871679 |
02m58.81s |
| 55 |
A |
26/05/2598 |
0.9895234 |
02m27.78s |
| 56 |
A |
06/06/2616 |
0.9916211 |
01m58.16s |
| 57 |
A |
17/06/2634 |
0.9935042 |
01m29.84s |
| 58 |
A |
27/06/2652 - 28/06/2652 |
0.9950354 |
01m05.79s |
| 59 |
A |
09/07/2670 |
0.9961687 |
00m47.26s |
| 60 |
A |
19/07/2688 |
0.9967399 |
00m36.25s |
| 61 |
A |
31/07/2706 -01/08/2706 |
0.9960352 |
00m.36.88s |
| 62 |
P |
11/08/2724 |
0.8822576 |
|
| 63 |
P |
22/08/2742 |
0.7560645 |
|
| 64 |
P |
01/09/2760 |
0.6399250 |
|
| 65 |
P |
13/09/2778 |
0.5318151 |
|
| 66 |
P |
23/09/2796 |
0.4338706 |
|
| 67 |
P |
04/102814 |
0.3469499 |
|
| 68 |
P |
15/10/2832 |
0.2725393 |
|
| 69 |
P |
26/10/2850 |
0.2098505 |
|
| 70 |
P |
05/11/2868 |
0.1587829 |
|
| 71 |
P |
17/11/2886 |
0.1194801 |
|
| 72 |
P |
28/11/2904 |
0.0907818 |
|
| 73 |
P |
09/12/2922 |
0.0696946 |
|
| 74 |
P |
20/12/2940 |
0.0570489 |
|
| 75 |
P |
31/12/2958 |
0.0487713 |
|
| 76 |
P |
10/01/2977 |
0.0452276 |
|
| 77 |
P |
22/01/2995 |
0.0403169 |
|
On remarque que cette suite n'est pas complète, en effet le canon d'éclipse de l'IMCCE s'arrête en 2999, il y a probablement des éclipses de la suite qui sont postérieures à cette date. Malgré cela on dépasse la valeur moyenne de 72 éclipses. Et l'on est assez loin des valeurs moyennes, ainsi le nombre d'éclipses partielles de la partie croissante est de 21, la moyenne donne 12 ! On constate également que toutes les éclipses centrales sont des éclipses annulaires, donc l'arc parcouru par les conjonctions lunaires est au voisinage de l'apogée. L'éclipse du 31 mai 2003 est la première éclipse centrale de la partie croissante de la suite, on peut donc en déduire qu'elle a lieu après le passage au nœud et relativement longtemps après ce passage. De plus elle est proche d'un des pôles terrestre. On ne peut pas savoir si la suite est au nœud ascendant ou descendant de l'orbite lunaire. Pour cela il suffit de connaître la latitude de la Lune à la conjonction pour une seule éclipse de la suite. Cette longitude est positive pour l'éclipse du 31 mai donc cette suite longue est au nœud ascendant et l'éclipse du 31 mai 2003 est proche du pôle nord terrestre et les éclipses de la suite vont parcourir le globe terrestre du nord au sud.
Les éphémérides de la Lune nous donnent les informations suivantes :
- le 28/05/2003 à 13h 04m 44s UT : la Lune à l'apogée (distance maximale à la Terre) d=406168 km, diam. app. =29.5'.
- le 30/05/2003 à 08h 32m 17s UT : la Lune passe par le nœud ascendant de son orbite, long. moyenne = +59° 30,9'.
- le 31/05/2003 à 04h 08m 18s UT : maximum de l'éclipse annulaire de Soleil.
- le 31/05/2003 à 04h 19m 51s UT : Nouvelle Lune.
On constate que le maximum de l'éclipse a bien lieu entre le passage et la conjonction, qu'il est proche de la conjonction (11m 33s) mais éloigné du passage au nœud (19h 36m 1s). L'éclipse est proche du passage de la Lune à l'apogée elle est donc annulaire.
Les éclipses anciennes
Introduction
 Introduction
Introduction
Dans cette section nous étudions quelques éclipses anciennes de Lune ainsi que leur prédiction et observation.
Visibilité des éclipses anciennes à l'oeil nu
L'Astronomie des Césars fut publiée par Petrus Apianus en 1540. Dédiée à Charles Quint et à son frère Ferdinand, l'Astronomie des Césars permet de déterminer les positions planétaires, ainsi que les éclipses, pour une période comprise entre 7000 av. J.-C. et 7000 apr. J.-C. ! Apianus utilise à la perfection l'usage des disques mobiles, ou " volvelles ". Des fils de soie permettent de lire les graduations sur les cadrans extérieurs. Les calculs sont effectués en utilisant les théories de Ptolémée. La figure ci-dessous nous montre une des pages dédiées au calcul des éclipses de Lune. On y voit la Lune, les cônes d'ombre et de pénombre de la Terre représentés avec des proportions assez bonnes.
Difficilement décelable à l'œil nu les éclipses de Lune par la pénombre ne seront pas observées avant l'apparition de la lunette astronomique, il convient malgré tout de signaler l'observation d'une éclipse par la pénombre par les Babyloniens le 1 août -187 (188 av. J.-C.). Une étude des observations des éclipses de Lune publiées par les chroniqueurs arabes médiévaux faite par Said et Stephenson en 1991 montre que l'on a des observations à l'œil nu d'éclipses partielles par l'ombre jusque des grandeurs de 0,28 et de 0,12.
Les éclipses anciennes
Les Babyloniens surent prédire la date et la visibilité des éclipses de Lune relativement tôt, on dispose d'un texte datant du règne de Ukin-zer (731 av. J.-C. - 729 av. J.-C.) où figure la prédiction de l'éclipse de Lune du 9 avril -730 avec la mention de son invisibilité à Babylone. On distingue deux types de sources, les éclipses babyloniennes décrites par Ptolémée dans l'Almageste, elles sont au nombre de dix :
| Date de l'éclipse |
Type de l'éclipse |
| 19 mars - 720* |
Totale (1,49) |
| 8 mars - 719* |
Partielle (0,08) |
| 1 septembre - 719 |
Partielle (0,46) |
| 22 avril - 620 |
Partielle (0,18) |
| 16 juillet - 522 |
Partielle (0,56) |
| 19 novembre -501* |
Partielle (0,22) |
| 25 avril - 490 |
Partielle (0,12) |
| 23 décembre - 382* |
Partielle (0,23) |
| 18 juin - 381* |
Partielle (0,51) |
| 12 décembre - 381* |
Totale (1,50) |
(*) Ces observations ont été utilisées par Ptolémée pour calculer les variations de l'anomalie de la Lune. En plus de ces observations, Ptolémée donne six autres observations d'éclipses de Lune dont cinq ont été faites à Alexandrie et une à Rhodes.
L'autre source d'observations d'éclipses de Lune par les Babyloniens est constituée de textes cunéiformes. On y dénombre une soixantaine d'éclipses réparties entre 695 av. J.-C. et 67 av. J.-C.
Les données d'observations d'éclipses de Lune par les Chinois sont plus tardives, elles sont réparties entre l'an 434 et l'an 1280, les données d'observations d'éclipses de Lune par les Arabes sont comprises entre l'an 854 et l'an 1019. La totalité de ces observations a été utilisée, avec les observations d'éclipses de Soleil, pour déterminer les écarts entre le Temps universel et le Temps terrestre durant les siècles passés.
Quelques éclipses historiques
L'éclipse d'Alexandre
Cette éclipse totale de Lune (m =1,23) eu lieu le 20 septembre -330 (331 av. J.-C.), à l'époque des combats entre Alexandre le Grand et les forces perses de Darius III, à Gaugamèles près d'Arbèles. La vue de cette éclipse aurait désorganisé les forces perses et permis la victoire d'Alexandre 11 jours plus tard (Plutarque,Vie d'Alexandre, Livre XXXI). Cette éclipse est également mentionnée par Pline l'Ancien (23 - 79 ap. J.-C.) dans son Histoire Naturelle (Livre II), selon Pline cette éclipse fut également visible en Sicile au lever du Soleil alors qu'elle a eu lieu la nuit à Arbèles. Pline utilise ce décalage horaire pour prouver que la Terre est ronde. L'éclipse d'Alexandre est également décrite par Arrien de Nicomédie (v. 95 - v. 175) dans L'Expédition d'Alexandre ou Anabase (Livre II) ; il situe la bataille d'Arbèles au mois de Pyaneptiôn lorsque Aristophane était Archonte d'Athènes. Une autre description intéressante de l'éclipse est celle donnée par Quinte-Curce (Ier s. apr. J.-C.) dans son Histoire d'Alexandre le Grand (Livre IV). C'est, en effet, une des plus anciennes allusions à l'aspect rougeâtre des éclipses totales de Lune.
L'éclipse de la chute de Constantinople
Cette éclipse partielle de Lune (m= 0,746) eu lieu le 22 mai de l'an 1453, elle mit fin au siège de Constantinople par les troupes turques du Sultan Mohammed II. La ville est vaillamment défendue par l'empereur Constantin Dragasès (1448-1453) et le Génois Giustiniani, une ancienne prophétie affirmait que la ville ne pourrait tomber qu'à la Lune croissante, alors qu'ils avaient déjà repoussé trois assauts avec succès et confiance, le lever de la pleine Lune éclipsée démoralisa les assiégés. La ville fut prise le 29 mai, sept jours plus tard. Cette victoire des Turcs sur les forces chrétiennes marque la fin de l'empire byzantin et le début de l'empire ottoman.
L'éclipse de Colomb
Cette éclipse totale de Lune (m=1,097) eu lieu le 29 février de l'an 1504. Lors de son quatrième voyage Christophe Colomb, échoua sur les côtes de la Jamaïque. Suite à la mutinerie d'une partie de son équipage qui déroba une partie de ces réserves, Christophe Colomb se trouva à court de vivres, les indiens refusant de l'approvisionner. Christophe Colomb prédit aux indiens une éclipse totale de Lune trois jours avant sa venue et la présenta comme un signe céleste du mécontentement du Dieu des chrétiens. L'éclipse eu lieu effectivement la nuit du 29 février est fut, nous dit Christophe Colomb, d'un rouge sombre. Fortement impressionnés par ce phénomène céleste, les indiens ravitaillèrent Christophe Colomb et son équipage jusqu'à l'arrivée des secours, quatre mois plus tard. Christophe Colomb ne cite pas ses sources pour la détermination de cette éclipse. À cette époque trois sources étaient possibles : les éphémérides et Calendarium de Regiomontanus (pour Nuremberg), l'Almanach Perpetuum d'Abraham Zacuto (pour Salamanque) et enfin le Lunarium de Bernard Granollachs (pour Barcelone). Christophe Colomb a vraisemblablement utilisé le Calendarium de Regiomontanus. La Lune se lève éclipsée, C. Colomb va mesurer la durée de l'éclipse, cinq sabliers depuis le coucher du Soleil, et va en déduire la longitude du lieu. Dans le calcul de cette longitude, il va commettre une erreur importante de 37°.
Rotondité de la Terre
Aristote (384 - 322 av. J.-C.) dans le Traité du ciel (Livre II, 13) nous informe que les Pythagoriciens, notamment Philolaos (~470 - ~390 av. J.-C.), avaient observé qu'il y avait plus d'éclipses de Lune que d'éclipses de Soleil, ils avaient expliqué ce phénomène en supposant l'existence d'une seconde Terre, l'anti-Terre, située à l'opposé de la Terre par rapport à un feu central et qui venait s'interposer entre le Soleil et la Lune. Cette anti-Terre n'était donc pas visible de la Terre et doublait le nombre d'éclipse de Lune. Cette explication, bien qu'étonnée, prouve que les Pythagoriciens avaient bien compris le mécanisme des éclipses, notamment que les corps célestes sont sphériques et que certains sont lumineux et d'autres plus ou moins opaques.
L'observation des éclipses de Lune a été utilisée par Aristote pour prouver que la Terre était ronde, ainsi dans le Traité du ciel (Livre II, 14) on peut lire "Lors des éclipses, la Lune a toujours pour limite une ligne courbe : par conséquent, comme l'éclipse est due à l'interposition de la Terre, c'est la forme de la surface de la Terre qui est cause de la forme de cette ligne". On remarquera que cette preuve n'est pas suffisante pour prouver la sphéricité de la Terre, un cylindre et un disque ont également des ombres circulaires. Le dessin ci-dessous, qui illustre la démonstration d'Aristote, est extrait de la Cosmographie de Petrus Apianus (1581).

Crédit : Bibliothèque de l'Observatoire de Paris
Le calcul de la distance Terre-Lune
Introduction
 Introduction
Introduction
Cette dernière section est purement mathématiques, elle présente un des calculs effectués par Aristarque de Samos dans son traité sur la grandeur et la distance du Soleil et de la Lune. Puis nous étudions les deux observations effectuées par Ptolémée et décrites dans l'Almageste, ces observations permettent de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil. On compare à cette occasion les valeurs calculées par Ptolémée avec les valeurs actuelles.
Par Aristarque de Samos
Aristarque de Samos (310 - 230 av. J.-C.) fut l'élève de Straton de Lampsaque, il est l'auteur du premier système héliocentrique, système décrit dans son livre "Les Hypothèses" (disparu) cité par Archimède dans son traité de l'Arénaire. Aristarque est également l'auteur du traité sur la grandeur et la distance du Soleil et de la Lune.
Pour le calcul des distances Terre-Lune et Terre-Soleil, il fait les hypothèses suivantes :
- 1. La Lune reçoit la lumière du Soleil.
- 2. La Terre peut être considérée comme un point et comme le centre de l'orbite de la Lune.
- 3. Lorsque la Lune nous parait dikhotome (coupée en deux portions égales), elle offre à nos regards son grand cercle, qui détermine la partie éclairée et la partie obscure de cet astre.
- 4. Lorsque la Lune nous parait dikhotome, sa distance du Soleil est moindre du quart de la circonférence, de la trentième partie de ce quart.
- 5. La largeur de l'ombre est de deux Lunes.
- 6. L'arc soutendu dans le ciel par la Lune est la quinzième partie d'un signe.
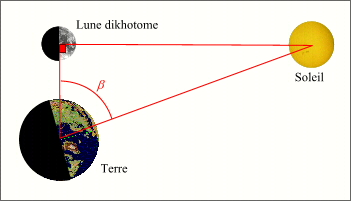
L'hypothèse 4 d'Aristarque
Crédit : IMCCE/Patrick Rocher
Comme on le constate certaines de ces hypothèses sont fausses, l'hypothèse 4 revient à donner à l'angle β la valeur de 87°. Cette erreur explique son l'erreur sur le calcul de la distance Terre-Soleil. L'hypothèse 6 donne à la Lune un diamètre de 2°, valeur quatre fois trop forte.
À partir de ces hypothèses, Aristarque va déduire que la distance Soleil-Terre est supérieure à 18 fois la distance Terre-Lune et inférieure à 20 fois la distance Terre-Lune. Il déduit de ces proportions les valeurs suivantes :
- le diamètre lunaire est inférieur à 2/45 distance Terre-Lune et supérieur à 1/30 distance Terre-Lune.
- le diamètre solaire est inférieur à 43/6 diamètres terrestres et supérieur à 19/3 diamètres terrestres.
- le diamètre terrestre est inférieur à 60/19 diamètres lunaires et supérieur à 108/43 diamètres lunaires.
 Remarque
Remarque
Il convient de remarquer qu'à l'époque d'Aristarque les Grecs n'avaient aucune notion de trigonométrie, les premières tables de cordes sont attribuées à Hipparque. C'est pourquoi Aristarque ne tire pas directement la valeur du rapport des distances Terre-Lune et Terre-Soleil de l'angle β, mais encadre cette proportion grâce à des considérations purement géométriques.
On trouve dans la littérature et sur le web de nombreux "exemples" de la détermination de la distance Terre-Lune par Aristarque, avec des hypothèques qui sont très variées (ombre cylindrique, ombre de trois diamètres lunaires, diamètre apparent de la Lune égal à 30'....) et utilisant des méthodes trigonométriques. C'est fort dommage car les méthodes employées par Aristarque sont remarquables et ont un intérêt pédagogique certain.
On peut consulter, sur le site Gallica (gallica.bnf.fr) de la Bibliothèque Nationale, une version française du Traité d'Aristarque de Samos Sur les grandeurs et les distances du Soleil et de la Lune traduite du grec par le Comte de Fortia d'Urban et édité en 1823.
On trouve dans un passage d'Archimède qu'Aristarque a également utilisé la valeur d'une demi-degré pour le diamètre lunaire, l'usage de la valeur de 2° dans le traité Sur la grandeur et la distance du Soleil et de la Lune est parfois présenté comme une valeur hypothétique utilisée par l'auteur dans une démonstration qui se veut plus didactique que physique.
En savoir plus: Une des démonstrations d'Aristarque
 En savoir plus
En savoir plus
La démonstration suivante est issue de la traduction du Comte de Fortia d'Urban et se trouve dans la proposition VIII du Traité d'Aristarque. Pour rendre la démonstration plus lisible je l'ai retranscrite en termes mathématiques plus contemporains.
La proposition
La proposition VIII est la suivante : La distance à laquelle le soleil se trouve de la terre est plus grande dix-huit fois, mais moindre vingt fois que celle à laquelle la lune se trouve de la terre.
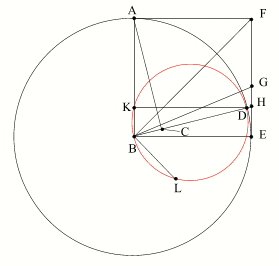
Crédit : IMCCE/Patrick Rocher
La démonstration
Soit A le centre du Soleil, B le centre de la Terre et C le centre de la Lune. Traçons le cercle (c) de centre B et de rayon AB, le rayon BD passant par C et faisant un angle de 3° avec le rayon BE perpendiculaire à BA (l'angle CBE est la trentième partie de l'angle droit). On construit le carré ABEF, ainsi que sa diagonale BF. Soit BG la bissectrice de l'angle EBF.
L'angle CBE est la trentième partie d'un angle droit (90°/30) et l'angle GBE est le quart d'un angle droit (90°/4), donc l'angle GBE vaut les 15/2 de l'angle CBE. Le rapport de EG sur EH est plus grand que le rapport des deux angles GBE et CBE, donc plus grand que 15/2.
BF est la diagonale du carré ABEF, donc le carré de BF est le double du carré de BE. De plus le carré construit sur FG est aussi le double du carré construit sur EG.
Or comme 49 est inférieur au double de 25, le carré de FG/EG = 2 est supérieur à 49/25, le rapport FG/EG est donc supérieur à 7/5.
Donc EF/EG = (EG+GF)/EG = 1 + GF/EG est supérieur à 12/5 ou 36/15.
Ainsi EG/EH est plus grand que 15/2 et EF/EG est supérieur à 36/15, donc EF/EH est supérieur à 18.
Or EF = BE, donc BE/EH est supérieur à 18, et comme BH est supérieur à BE, BH/EH est également supérieur à 18. Or les triangles ABC et EBH sont semblables, donc les rapports BH/EH et AB/BC sont égaux et l'on a bien BA supérieur à 18 BC.
La distance Terre-Soleil est supérieure à 18 fois la distance Lune-Soleil.
Reste à prouver que ce rapport est inférieur à 20. Pour cela traçons la parallèle à BE, cette parallèle coupe AB en K. Traçons le cercle passant par les points BDK et soit L le point du cercle tel que LB soit le côté d'un hexagone inscrit dans ce cercle.
L'angle DBK est égal à l'angle DBE égal à la trentième partie d'un angle droit, l'arc de cercle BK vaut le double donc la quinzième partie d'un angle droit ou encore la soixantième partie de la circonférence.
Or BL est la sixième partie de cette même circonférence; donc l'arc BL est dix fois plus grand que l'arc BK. Or le rapport des cordes BL/BK est inférieur au rapport des arcs BL/BK, donc la corde BL est inférieure à dix fois la corde BK.
Or BD est égal à deux BL, donc BD est inférieur à 20 BK. Or les triangles DKB et ABC sont semblables donc BD/BK = AB/BC, donc AB est bien inférieur à 20 BC.
 Remarque
Remarque
Bien évidemment, si l'on connaît la trigonométrie, cette longue démonstration élégante est remplacée par une simple équation à savoir : AB/BC = 1/sin 3° d'où AB/BC = 19,10.
Par Claude Ptolémée
Ptolémée, dans l'Almageste (livre V chapitre 14), nous décrit deux méthodes permettant de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil.
Le calcul du diamètre lunaire
Pour le calcul du diamètre apparent de la Lune, Ptolémée utilise deux éclipses de Lune observées à Babylone. La première a eu lieu l'an 5 de l'ère de Nabopolassar, qui est l'année 127 de l'ère de Nabonassar, à la fin de la onzième heure du 27 au 28 du mois égyptien Athyr (troisième mois de l'année). Cette date correspond à la nuit du 21 au 22 avril -620 (621 av. J.-C.). Ptolémée nous dit "on vit à Babylone la Lune commencer à s'éclipser; et la plus grande phase de cette éclipse fut du quart du diamètre dans la partie méridionale de l'astre". Puis il calcule la position de la Lune sur son orbite pour l'instant du maximum de l'éclipse et trouve qu'elle se trouve à 9,5° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 48,5'. La seconde éclipse de Lune utilisée est celle de l'an 7 de Cambyse, c'est-à-dire l'an 225 de l'ère de Nabonassar, elle s'est produite à une heure avant minuit du 17 au 18 du mois égyptien Phamenoth, ce qui correspond à l'éclipse du 16 juillet -522 (523 av. J.-C.); Ptolémée nous dit "on vit à Babylone la lune s'éclipser de la moitié de son diamètre dans la partie boréale" et il calcule qu'au maximum de l'éclipse la Lune est à 7,8° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 40,6'. Ptolémée calcule également que les deux éclipses ont lieu sensiblement lorsque la Lune est à une même distance angulaire de son apogée, donc que les diamètres lunaires apparents sont sensiblement identiques, alors la différence des distances à l'axe des cônes est égale au quart de diamètre lunaire, Ptolémée en déduit que le diamètre lunaire est de l'ordre de 31,3'. À partir de la deuxième éclipse, Ptolémée calcule également le rayon du cône d'ombre en fonction du rayon apparent de la Lune et il trouve que ce rayon "est un peu moindre que le double et 3/5 du rayon de la Lune".
Les tableaux suivants donnent les valeurs calculées avec les théories actuelles et les valeurs données par Ptolémée dans l'Almageste.
L'éclipse des 21 et 22 avril -620
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,1818685 |
|
| Diamètre lunaire apparent |
29,51' |
|
| Instant du maximum |
1h56,2m UT |
|
| Instant du maximum en heure locale |
4h54,2m |
environ 6 h |
| Distance centre de la Lune axe des cônes |
48'31,91" |
48'30" |
| Longitude de la Lune |
204°53'31,5" |
205°32' |
| Elongation par rapport au noeud |
8,77° |
9,3° |
| Longitude par rapport à l'apogée |
339°6' |
340°7' |
L'éclipse du 16 juillet -522
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,5615770 |
|
| Diamètre lunaire apparent |
29,63' |
|
| Instant du maximum |
20h28,8m UT |
|
| Instant du maximum en heure locale |
23h26,8m |
environ 23h |
| Distance centre de la Lune axe des cônes |
37'21,56" |
40'40" |
| Longitude de la Lune |
287°0'41,68" |
288°14' |
| Elongation par rapport au noeud |
6,75° |
7,8° |
| Longitude par rapport à l'apogée |
31°55' |
28°5' |
Ptolémée garde cette valeur de 31' 20" pour le diamètre lunaire et la considère comme constante alors qu'il tient compte des variations de la distance Terre Lune. Il estime le maximum de cette distance à 64 +1/6 rayons terrestres. La valeur moyenne étant de 59 rayons terrestres et il représente le mouvement de la Lune à l'aide d'un cercle déférent de 59 rayons terrestres et d'un épicycle de 5 +1/6 rayons terrestres. En faisant l'hypothèse que le diamètre apparent du Soleil est égal au diamètre apparent de la Lune à son apogée, il déduit de ces valeurs la distance Terre-Soleil et la distance de la Terre au sommet de son cône d'ombre. Il trouve une distance Terre Soleil de 605 rayons terrestres et une distance Terre sommet du cône d'ombre de 134 rayons terrestres.
Problèmes et QCM
Introduction
 Introduction
Introduction
Ce chapitre regroupe tous les QCMs (exercices d'auto-évaluation classés par thèmes) correspondant à l'intégralité du chapitre Soleil Terre Lune Phénomènes, ainsi que plusieurs problèmes avec leurs rappels de cours éventuellement.
QCM Soleil-Terre-Lune
QCM sur les calendriers
QCM sur les mouvements de la Terre et de la Lune
QCM sur les saisons et les levers couchers
QCM sur les éclipses
QCM sur la durée des éclipses
Exercice 1 : Marco et Polo en ULM
Énoncé
 Marco et Polo en ULM
Marco et Polo en ULM
Question 1)
Marco et Polo décident de faire le tour du monde en ULM.
Ils partent de Paris vers l'est le mercredi 27 mars 2002 à 10h du matin en temps légal français.
Ils arrivent à Paris le samedi 13 avril à 10h du matin en temps légal français.
Dans les calculs, on supposera que la Terre est sphérique et que son rayon est 6378 km ; on supposera aussi qu'ils ont fait le tour de la Terre en suivant le parallèle de Paris dont la latitude sera prise égale à 49° et l'on négligera l'altitude de l'ULM.
En sachant que l'on est passé de l'heure d'hiver (UTC + 1h) à l'heure d'été (UTC +2h) la nuit du 31 mars 2002, quelle est la vitesse moyenne de leur tour du monde ?
Combien ont-ils observé de levers de Soleil durant leur voyage ?
S'ils avaient fait le tour du monde à la même vitesse mais en partant vers l'ouest, quand seraient-ils arrivés et combien de levers de Soleil auraient-ils observés ?
Calculer la longueur du parallèle puis calculer la vitesse moyenne
Le passage à l'heure d'été consiste à supprimer une heure dans la nuit du samedi 30 au dimanche 31.
Exercice 2 : Marco et Polo font du bateau
Énoncé
 Marco et Polo font du bateau
Marco et Polo font du bateau
Question 1)
En l'an 1867, Marco et Polo décident de réitérer l'exploit de Christophe Colomb et de traverser l'Atlantique sur leur radeau le « Kicoolpa », ils partent des côtes françaises à la mi-février. La traversée se déroule bien, sauf vers la fin où ils sont pris dans une terrible tempête. Durant cette tempête ils perdent une grande partie de leur matériel et échouent finalement sur une île inconnue le mardi 19 mars 1867 au soir.
Or ils ont réussi à sauver de la tempête un précieux Annuaire du Bureau des longitudes pour l'année en cours.
Dans cet annuaire, ils trouvent (page 12), les éphémérides du Soleil à Paris au mois de mars
| 1867 Mars |
Lever |
Coucher |
Passage au méridien de Paris |
| 19 mars : mardi : St Joseph |
6h 8m |
18h 9m |
12h 8m 1s |
| 20 mars : mercredi : St Joachim |
6h 6m |
18h 11m |
12h 7m 43s |
| 21 mars : jeudi : St Benoît
Printemps à 1h 55m |
6h 3m |
18h 12m |
12h 7m 25s |
| 22 mars : vendredi : St Emile |
6h 1m |
18h 14m |
12h 7m 6s |
| 23 mars : samedi : St Victorien |
5h 59m |
18h 15m |
12h 6m 48s |
Seuls les instants des passages sont utiles pour notre problème.
Dans cette éphéméride les instants sont donnés en temps moyen du méridien de Paris, le Soleil apparent ne tournant pas uniformément autour de la Terre, l'instant du passage au méridien du lieu (midi au Soleil) exprimé en temps moyen diffère de 12h. Ainsi le 19 mars le Soleil passe au méridien (midi au Soleil) lorsque qu'une montre donnant l'heure en temps moyen de Paris indique 12h 8m 1s.
Dans cette éphéméride, ils trouvent également (page 32) qu'une éclipse partielle de Lune aura lieu 20 mars 1867, avec les horaires suivants :
| Phénomène |
Instant en temps moyen de Paris |
| Entrée dans l'ombre de la Terre |
7h 25m 27s |
| Maximum de l'éclipse |
8h 58m 15s |
| Sortie de l'ombre de la Terre |
10h 30m 57s |
Cette éclipse n'est pas visible à Paris (il fait jour au moment de l'éclipse).
Polo a sauvé la montre gousset de son oncle Anatole, il l'avait mise à l'heure de Paris à son départ de France et a toujours pris soin de la remonter chaque jour, mais cette montre, très précise à Terre, à la fâcheuse habitude de prendre du retard lorsqu'elle est ballottée par les flots.
Dans la seconde partie de la nuit du 19 au 20 mars, ils observent le début de l'éclipse partielle de Lune, c'est-à-dire l'entrée de la Lune dans l'ombre de la Terre. La montre de l'oncle Anatole indique alors 7h 2m 17s. Ils ne peuvent observer la fin de l'éclipse, la Lune se couchant éclipsée.
Le jour suivant, ils construisent un gnomon, à l'aide d'un manche à balai planté verticalement dans le sol, à l'aide d'un cordeau, ils tracent un cercle autour du manche à balai et notent le matin et l'après-midi l'intersection de l'ombre du balai avec le cercle. La bissectrice de l'angle formé par ces deux directions leur donne la direction du méridien nord-sud du lieu.
Le lendemain, le 21 mars, jour de l'équinoxe de printemps, ils notent la longueur de l'ombre à l'instant où le Soleil passe par le méridien, à cet instant la montre de l'oncle Anatole indique 15h 57m 21s. Et le rapport de l'ombre du balai sur la longueur du balai est égal à 0,244. L'ombre est dirigée vers le nord.
Hourra ! S'écrit Marco, nous pouvons connaître notre latitude, notre longitude par rapport à Paris et je sais de combien retarde la montre de l'oncle Anatole.
Quelles sont les coordonnées de l'île et quel est le retard de la montre de l'oncle Anatole ?
On donnera la longitude par rapport au méridien de Paris et la latitude en degrés, minutes et secondes. Attention il faut donner les secondes pour que les résultats soient valables.
Le lendemain (22 mars) Marco décide de mettre sa montre à l'heure en temps moyen local de l'île au moment du passage au méridien du Soleil. Quelle heure affichera-t-il à sa montre à cet instant ?
Hypothèses supplémentaires et rappels
On supposera que la montre ne prend plus de retard une fois les hommes à Terre.
Les dessins et définitions ci-dessus ont pour but de vous aider dans la résolution du problème :
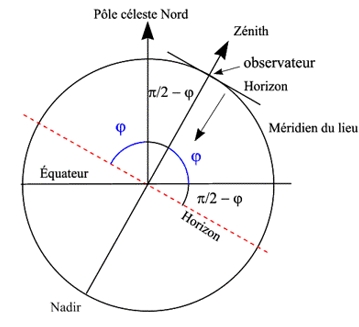
Crédit :
P. Rocher / Observatoire de Paris
On suppose la Terre sphérique, le dessin ci-dessus représente la coupe méridienne de la Terre pour un lieu situé sur le méridien et de latitude φ.
On suppose que la vitesse angulaire en longitude du Soleil apparent est constante d'un passage au méridien de Paris à l'autre.
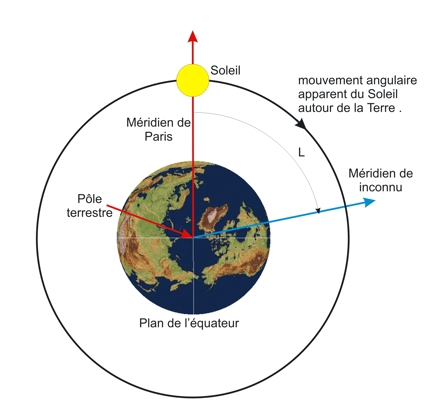
Le dessin ci dessus représente une vue polaire du mouvement angulaire apparent du Soleil autour de la Terre (considérée comme fixe).
Crédit :
P. Rocher
On rappelle que le temps moyen est donné par une horloge battant la seconde et qu'un jour moyen comporte 24h (86400s). On rappelle que la différence de temps moyen entre deux lieux est égale à la différence des longitudes (exprimée en heure) entre ces deux lieux.
On rappelle qu'à l'instant des équinoxes la Terre est sur la droite définie par l'intersection de son plan orbital autour du Soleil et de l'équateur terrestre. Donc à cet instant le Soleil apparent est dans l'équateur terrestre, on suppose qu'il y reste toute la journée de l'équinoxe (en réalité il n'y est qu'au moment de l'équinoxe).
Enfin on rappelle qu'une éclipse de Lune est un phénomène indépendant du lieu d'observation, il suffit que la Lune soit levée pour l'observer.
 Remarque
Remarque
Toutes ces données sont exactes et sont issues de l'Annuaire de 1867. Seul le voyage de Marco et Polo est de la fiction !
Réponses aux QCM
pages_types-eclipses/stlp-qcm-type-eclipse.html
QCM
'QCM sur les différents types d'éclipses'
- Question 1
Solution : réponse 1)
(
Les éclipses centrales annulaires, les éclipses centrales totales et les éclipses centrales annulaire-totales.
)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 1)
- Question 5
Solution : réponse 2)
pages_nombre-eclipses-soleil/stlp-exercice-02-eclipsesol.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 5)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 1)
- Question 5
Solution : réponse 2)
- Question 6
Solution : réponse 2)
pages_stlp-qcm/stlp-qcm-calendriers.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 3)
- Question 4
Solution : réponse 2)
Solution : réponse 3)
Solution : réponse 4)
pages_stlp-qcm/stlp-qcm-mvmts-terre-lune.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 3)
- Question 3
Solution : réponse 1)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 2)
- Question 6
Solution : réponse 1)
- Question 7
Solution : réponse 1)
- Question 8
Solution : réponse 1)
- Question 9
Solution : réponse 3)
- Question 10
Solution : réponse 2)
- Question 11
Solution : réponse 2)
- Question 12
Solution : réponse 2)
- Question 13
Solution : réponse 2)
- Question 14
Solution : réponse 3)
- Question 15
Solution : réponse 2)
pages_stlp-qcm/stlp-qcm-saisons-levers-couchers.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 3)
- Question 5
Solution : réponse 1)
- Question 6
Solution : réponse 2)
- Question 7
Solution : réponse 1)
pages_stlp-qcm/stlp-qcm-eclipses.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 2)
- Question 6
Solution : réponse 3)
- Question 7
Solution : réponse 1)
Solution : réponse 2)
- Question 8
Solution : réponse 2)
- Question 9
Solution : réponse 2)
Solution : réponse 3)
- Question 10
Solution : réponse 2)
- Question 11
Solution : réponse 2)
- Question 12
Solution : réponse 2)
pages_stlp-qcm/stlp-qcm-duree-eclipses.html
QCM
- Question 1
Solution : réponse 1)
Solution : réponse 2)
Solution : réponse 7)
- Question 2
Solution : réponse 3)
Solution : réponse 4)
Solution : réponse 7)
- Question 3
Solution : réponse 1)
Solution : réponse 2)
Réponses aux exercices
pages_stlp-problemes/stlp-probleme1-enonce.html
Exercice
'Marco et Polo en ULM'
 Introduction
Introduction Remarque
Remarque








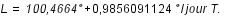
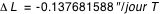





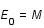
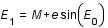
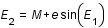
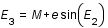 et ainsi de suite.
et ainsi de suite.
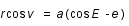
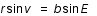
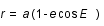




















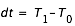 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 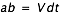 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).

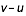 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.

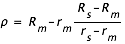
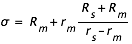














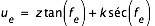
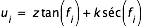




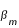 = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).

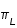 .
.
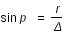 ,
, 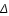 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.

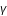 : l' angle S0M0S.
: l' angle S0M0S.
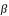 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
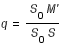 soit
soit 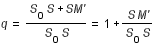
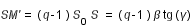 avec
avec 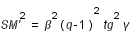
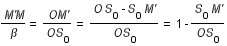
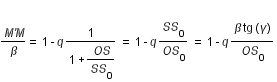
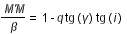
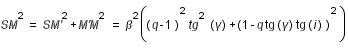 (1)
(1)
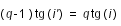
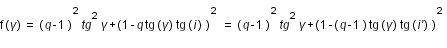
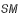 est minimum lorsque
est minimum lorsque 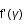 la dérivée de f est nulle
la dérivée de f est nulle
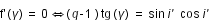 (2)
(2)
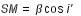 (3)
(3)
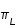 et
et 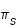 de la Lune et du Soleil.
de la Lune et du Soleil.
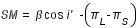 (4)
(4)
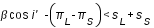
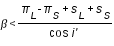 (5)
(5)
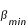 du second membre de (5) est obtenue avec
du second membre de (5) est obtenue avec 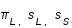 minimales et
minimales et 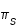 maximale, la valeur supérieure
maximale, la valeur supérieure 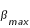 est obtenue avec
est obtenue avec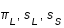 maximales et
maximales et 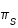 minimale.
minimale.
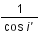
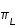
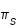
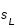
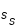
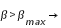 pas éclipse
pas éclipse
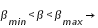 éclipse possible
éclipse possible
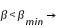 éclipse certaine
éclipse certaine
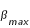 = 1° 34' 45,69" et
= 1° 34' 45,69" et 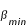 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 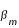 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
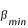 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 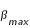 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 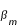 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).















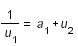
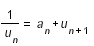

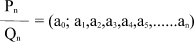
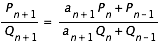
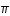
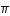 = 3,141592654
= 3,141592654












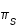
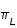
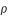
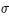

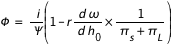


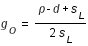
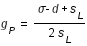
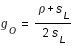 .
.









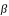 : la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
: la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
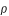 (et de pénombre
(et de pénombre 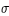 ) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
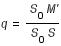 soit
soit 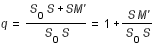
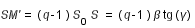 avec
avec 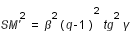
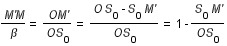
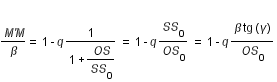
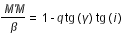
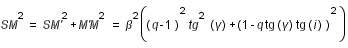 (1)
(1)
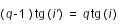
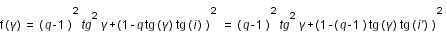
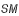 est minimum lorsque
est minimum lorsque 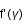 est nulle
est nulle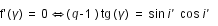 (2)
(2)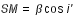 (3)
(3)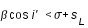
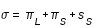
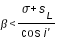 (4)
(4)
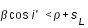
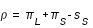
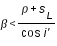 (5)
(5)
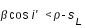
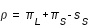
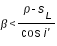 (6)
(6)
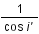
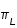
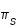
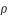 *
*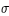 *
*