S'évaluer

Durée d'effondrement

Difficulté : ☆☆ Temps : 20 min

L'échelle de temps dynamique d'un objet autogravitant donne un bon ordre de grandeur de la durée caractéristique de l'éventuel effondrement de cet objet.

	Masse (kg)	Rayon (km)
Soleil	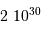$2\ 10^{30}$	700 000
Étoile à neutrons	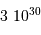$3\ 10^{30}$	10
Nuage d'hydrogène moléculaire	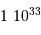$1\ 10^{33}$	10 AL

Question 1)

Rappeler l'expression de cette échelle de temps, fonction de la masse 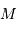, du rayon 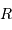et de la constante gravitationnelle $\cal G$ .

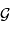[2 points]

Question 2)

Calculer l'échelle de temps pour les 3 objets proposés. Commenter.

[3 points]

Quelle source d'énergie ?

Difficulté : ☆☆ Temps : 20 min

Question 1)

Estimer le réservoir d'énergie gravitationnelle, fonction de la masse 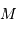, du rayon 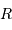du Soleil, et de la constante gravitationnelle 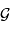$\cal G$ . Faire l'application numérique.

	Masse (kg)	Rayon (km)	Luminosité (W)
Soleil	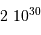$2\ 10^{30}$	700 000	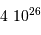$4 \ 10^{26}$

[2 points]

Question 2)

En déduire l'échelle de temps associée à ce réservoir d'énergie. Est-elle compatible avec l'âge du Soleil ?

[2 points]

Question 3)

On s'intéresse au réservoir d'énergie nucléaire. Le rendement énergétique de la fusion de l'hydrogène en hélium est de 0.007, ce qui signifie que la fusion d'une masse 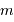d'hydrogène dégage une énergie 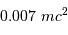$0.007\ mc^2$ . On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera. En déduire une estimation de la durée de vie du Soleil.

[2 points]