
|
L'effet de sélection dans l'observation de ces couples est très important. Deux catégories d'objets sont en particulier très difficile à observer : les binaires à longue période d'une part, et d'autre part les étoiles qui forment au contraire un système très serré.
La séparation caractéristique de tels couples varie d'une fraction d'unité astronomique à quelques centaines d'unités astronomiques, quand leurs périodes s'échelonnent de quelques années à plus d'un siècle. Les périodes plus longues (quelques siècles) ou les orbites plus grandes sont très difficiles à mettre en évidence, essentiellement pour des raisons de recul dans le temps.
Un grand intérêt de l'observation des étoiles binaires visuelles est que la mesure des paramètres apparents de l'orbite permet de calculer la masse des deux composantes du système, via la 3e loi de Kepler :
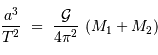
La définition du barycentre du système conduit à :
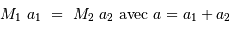
où 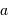 représente le demi-grand axe de l'orbite relative du corps de masse
représente le demi-grand axe de l'orbite relative du corps de masse 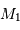 par rapport au corps de masse
par rapport au corps de masse 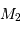 et
et 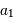 et
et 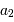 sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre
sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre 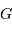 du système.
du système.
La mesure de 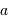 ,
, 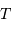 et de la position du barycentre du système (c'est-à-dire des demi-grands axes
et de la position du barycentre du système (c'est-à-dire des demi-grands axes 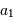 et
et 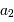 ) permet alors de déterminer
) permet alors de déterminer 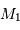 et
et 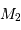 .
.