Excentricité limite dans les développements du problème à 2 corps

Auteurs: Alain Vienne, Stéphane Erard

Auteur: Alain Vienne

En mécanique céleste, il est quelque fois utile d'utiliser certaines formules du problème à 2 corps (ou problème keplerien) sous forme de développements. Cela permet, en théorie des perturbations, de faire des calculs analytiques.

Par exemple, l'"équation du centre", qui donne la position du corps sur son orbite en fonction du temps, est:

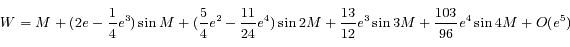
$W=M+(2e-\frac{1}{4}e^3)\sin M + (\frac{5}{4}e^2-\frac{11}{24}e^4)\sin 2M + \frac{13}{12}e^3 \sin3M + \frac{103}{96} e^4 \sin 4M +O (e^5)$

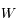est l'anomalie vraie, c'est à dire l'angle qui positionne le corps sur son orbite à partir de la direction du minimum de distance (péricentre ). 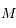est le temps ou plus précisément c'est l'anomalie moyenne 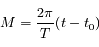$M=\frac{2\pi}{T} (t-t_0)$ avec 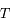la période, 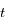le temps et 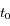t_0 l'instant de passage au péricentre. est l'excentricité.

Attention cette formule est bien une série entière en (mais tronquée à l'ordre 4). Cela aurait été plus net si on l'avait écrit comme:

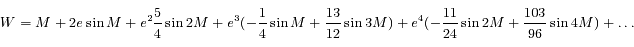
$W=M+2e \sin M + e^2 \frac{5}{4}\sin 2M + e^3 (-\frac{1}{4}\sin M + \frac{13}{12} \sin3M) + e^4 (-\frac{11}{24}\sin 2M + \frac{103}{96} \sin 4M) +\dots$

Mais, en fait, on préfère l'écriture en série de Fourier, c'est-à-dire:

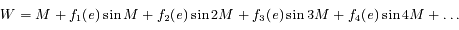
$W=M+ f_1(e) \sin M + f_2(e)\sin 2M + f_3(e) \sin3M + f_4(e) \sin 4M + \dots$

En tant que série de Fourier, la convergence ne pose pas de problème car la fonction à considérer est de classe 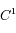C^1 par rapport à la variable 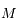. Seulement, dès que les 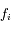f_i sont tronqués à un certain ordre en excentricité, cela revient à considérer la série entière.

L'exercice qui est proposé utilise le théorème de Lagrange pour montrer que la série entière ci-dessus (et toutes celles du problème des 2-corps) converge si 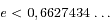$e<0,6627434\dots$ . Cela signifie que ces séries ne peuvent être utilisées que pour des excentricités bien en deça de cette valeur. Evidemment, la solution du problème à 2 corps elle-même existe quelque soit l'excentricité.

Théorème de Lagrange

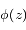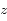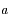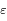Soit une fonction complexe $\phi (z)$ de la variable complexe . Soient et $\varepsilon$ des complexes.

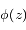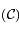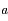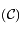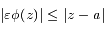
Si $\phi (z)$ est analytique à l'intérieur du contour $( \mathcal{C} )$ du plan complexe entourant le point avec $( \mathcal{C} )$ tel que : $| \varepsilon \phi (z) | \le |z-a|$

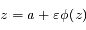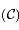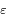Alors l'équation : $z=a+\varepsilon \phi (z)$ a une raçine développable dans l'intérieur de $( \mathcal{C} )$ en série entière de $\varepsilon$ :

$z= a + \sum_{n=1}^{\infty} \frac{\varepsilon ^n}{n!}\bigg[\frac{d^{n-1}}{dz^{n-1}}[\phi (z)]^n\bigg]_{z=a}$

Plus généralement, pour toute fonction 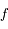analytique dans 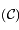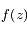$( \mathcal{C} )$ , f(z) peut aussi être développée:

$f(z)= f(a) + \sum_{n=1}^{\infty} \frac{\varepsilon ^n}{n!}\bigg[\frac{d^{n-1}}{dz^{n-1}}\bigg( \frac{df}{dz}[\phi (z)]^n \bigg) \bigg]_{z=a}$

Un autre exercice avec ce théorème est disponible ici.