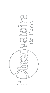Trajectoires dans l'espace des orbites

Le leggi di Keplero implicano che l’orbita di un pianeta sia un ellisse di cui uno dei fuochi sia occupato dalla stella genitrice. Questa orbita ellittica è caratterizzata da 5 parametri geometrici :

• 2 angoli per caratterizzare l’orientamento del piano dell’ellisse
• Su questo piano, un angolo per cratterizzare la direzione del semi-asse maggiore
• Il valore a di questo semi-asse maggiore
• Eccentricità e dell’elisse

Gli astronomi hanno l’abitudine di utilizzare dei parametri angolari legermenti diversi per caratterizzare il piano dell’orbita: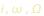

• i è chiamata inclinazione dell’orbita ed è l’angolo tra il piano dell’orbita e il piano del cielo ‘altrimenti 90° - i è l’angolo tra il piano dell’orbita e la “linea visuale” che congiunge l’osservatore al sistema planetario).
• 
• 

Il movimento del pianeta sulla sua orbita è caratterizzato dal periodo P di rivoluzione orbitale e dal istante * di passagio in un punto dato dell’orbita, per esempio il periastro... Per una data orbita il periodo dipende dalla massa della stella: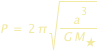

I metodi dinamici consistono nell’individuare la perturbazione indotta dalla rivoluzione orbitale del pianeta sul moto della stella. Questi movimenti sono regolati dalle leggi della meccanica celeste. La stella ed il pianeta girano tutti e due intorno al centro di gravità del sistema stella-pianeta. Per un pianeta situato a una distanza a dalla sua stella, la stella è a una distanza

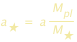
dal centro di massa del sistema. Per un orbita circolare del pianeta, a è costante e lo è anche 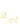, cosicche’ la stella segue una traiettoria circolare intorno al centro di massa.
Questo movimento si puo osservare in tre modi: