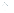|
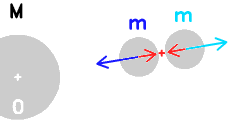
Il ragionamento di Roche, che riportiamo qui di seguito, riposa sull’ipotesi semplificatrice seguente : anche se il satellite è sferico, immaginaimolo costituito da due sfere di raggio r e di massa m. Basta pensare a due palle di neve sporche, ognuna di raggio r, mantenute insieme grazie alla forza di gravitazione universale che ognuna esercita sull’altra. Questa forza, che chiameremo  , è data dalla relazione di Newton : , è data dalla relazione di Newton :
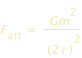
Consideriamo ora che il satellite sia piazzato a una distanza D di un pianeta di massa M e di raggio R. La forza d’attrazione F, tra il pianeta e la palla di neve la più vicina, sara più grande che la forza F’ tra il pianeta e la palla più lontana. La Forza F è data dalla relazione seguente :
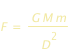
E la forza F’ è data da: :
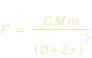
Le due palle risentiranno una forza risultante 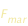 che tende a separarle. Questa forza equivale alla differenza delle forze F e F’. Si ha dunque : che tende a separarle. Questa forza equivale alla differenza delle forze F e F’. Si ha dunque :
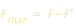 E, perchè D>>r :
E, perchè D>>r :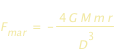
Ci sarà separazione delle due masse se la forza 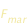 è superiore alla forza è superiore alla forza  . .
Ci sarà dunque separazione se :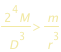
Rimpiazziamo la massa M con r 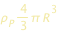 , dove , dove 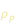 è la densita del pianeta, e la massa m con è la densita del pianeta, e la massa m con
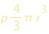 , dove , dove 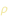 è la densita del satellite. è la densita del satellite.
C’è separazione se la distanza D è inferiore a 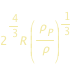
L’approssimazione è accetabile perchè 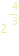 vale 2,51 mentre il valore esatto è 2,456 vale 2,51 mentre il valore esatto è 2,456
|
 Calcolo del limite di Roche
Calcolo del limite di Roche

 , è data dalla relazione di Newton :
, è data dalla relazione di Newton :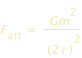
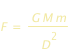
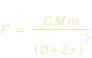
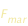 che tende a separarle. Questa forza equivale alla differenza delle forze F e F’. Si ha dunque :
che tende a separarle. Questa forza equivale alla differenza delle forze F e F’. Si ha dunque :
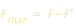 E, perchè D>>r :
E, perchè D>>r :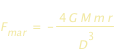
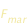 è superiore alla forza
è superiore alla forza  .
.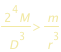
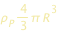 , dove
, dove 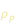 è la densita del pianeta, e la massa m con
è la densita del pianeta, e la massa m con
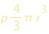 , dove
, dove 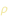 è la densita del satellite.
è la densita del satellite.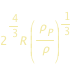
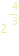 vale 2,51 mentre il valore esatto è 2,456
vale 2,51 mentre il valore esatto è 2,456