

Ex : loi de Wien |
Difficulté : ☆☆ Temps : 1h
Sachant que 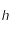 ,
, 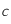 et
et 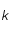 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 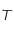 étant mesurée en degré Kelvin est aussi strictement positive, montrer que
étant mesurée en degré Kelvin est aussi strictement positive, montrer que 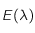 est de classe
est de classe 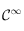 et est toujours strictement positive lorsque
et est toujours strictement positive lorsque 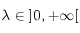 .
.
Montrer que les limites de 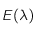 quand
quand 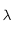 tend vers 0 et vers
tend vers 0 et vers 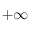 sont toutes les deux égales à zéro.
sont toutes les deux égales à zéro.
En déduire qu'il doit exister un maximum pour 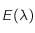 sur
sur 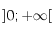 .
.
En effectuant le changement de variable 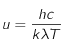 , montrer qu'étudier le signe de
, montrer qu'étudier le signe de 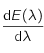 revient à étudier celui de
revient à étudier celui de 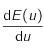 .
.
En déduire une condition sur 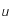 , de la forme
, de la forme 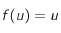 , pour que
, pour que 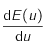 s'annule. On note
s'annule. On note 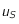 la solution de cette équation lorsqu'elle existe.
la solution de cette équation lorsqu'elle existe.
On peut monter par le théorème du point fixe dans 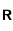 que
que 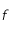 admet un point fixe et que la suite définie par
admet un point fixe et que la suite définie par 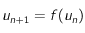 converge vers ce point fixe (voir Loi de Wien et théorème du point fixe). En prenant
converge vers ce point fixe (voir Loi de Wien et théorème du point fixe). En prenant 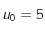 trouver une valeur
trouver une valeur 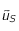 qui soit une valeur approchée de
qui soit une valeur approchée de 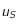 à
à 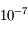 prêt.
prêt.
En déduire la relation 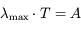 où
où 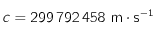 ,
, 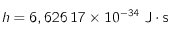 et
et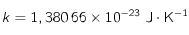 . Cette relation correspond à la loi de Wien pour les corps noirs.
Justifier l'utilisation de
. Cette relation correspond à la loi de Wien pour les corps noirs.
Justifier l'utilisation de 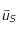 dans le calcul de la constante
dans le calcul de la constante 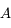 .
.