Auteur: Alain Vienne
On propose ici une application simple et directe du thèorème de Pythagore. Il faut le considérer ici comme une révision
des "années collège et lycée" de l'étudiant. Notre expérience d'enseignement montre que cela n'est pas inutile.
On considère un satellite à une certaine altitude. Il s'agit de savoir sur quelle partie de la Terre
il sera visible. Cet excercice peut s'appliquer directement pour savoir d'où est visible une
montagne.
L'exercice proposé dans la partie "intégrale de Rieman" est plus complet et calcule notamment la surface correspondante.
Auteur: Alain Vienne
 Zone visible d'une montagne ou d'un satellite
Zone visible d'une montagne ou d'un satellite
Difficulté : ☆
Temps : 20 mn
Question 1)
Soit un satellite artificiel de hauteur 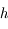 , sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
, sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
Question 2)
Le rayon de la Terre étant de 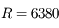 km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
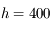 km?
km?
Auteurs: Arnaud Beck, Stéphane Erard
Quand le Soleil est au zénith, impossible de le regarder à l'oeil nu sans être ébloui voire même se brûler la rétine. Pourtant, le soir tombé, on peut admirer le Soleil couchant sans la moindre gêne.
Cela s'explique simplement par la diffusion des rayons solaires par les molécules de l'atmosphère. En effet, quand les rayons du Soleil rencontrent une molécule, une partie d'entre eux est déviée ou absorbée. Et plus le nombre de particules qu'ils rencontrent est grand, plus la proportion de rayons déviés est grande et l'énergie lumineuse reçue par l'observateur sera réduite d'autant.
Dans cet exercice, on propose de quantifier le nombre de particules rencontrées par un rayon de Soleil en fonction de sa position dans le ciel par rapport à un observateur potentiel.
Le parcours atmosphérique est également calculé dans le cas général.
Auteur: Arnaud Beck, Stéphane Erard
 Pourquoi peut-on regarder le Soleil couchant ?
Pourquoi peut-on regarder le Soleil couchant ?
Difficulté : ☆
Temps : 1h
Le nombre de particules atmosphériques rencontrées par un rayon de Soleil le long de son parcours est appelé densité de colonne, et est égal à :
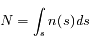
où 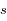 est la coordonnée le long du trajet du rayon et
est la coordonnée le long du trajet du rayon et 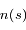 est la densité atmosphérique au point de coordonnée
est la densité atmosphérique au point de coordonnée 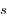 .
.
On peut approximer la densité atmosphérique à faible altitude (là où elle est la plus dense) par:
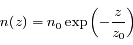
où 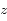 est l'altitude (mesurée verticalement),
est l'altitude (mesurée verticalement), 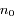 est la densité au niveau du sol, et
est la densité au niveau du sol, et 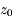 est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
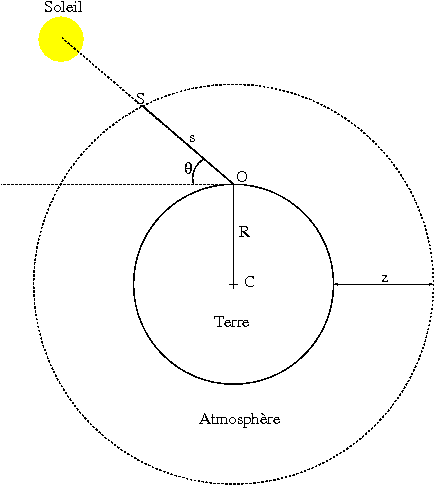
La figure ci-dessous représente la situation. Le centre de la Terre est au point C, l'observateur en O. Le point S représente le point de coordonnée 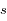 sur le trajet du rayon de Soleil, et d'altitude
sur le trajet du rayon de Soleil, et d'altitude 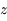 .
. 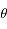 est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
Arrivée d'un rayon de Soleil sur Terre
Question 1)
Dans le cas du Soleil couchant (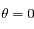 ), donner l'expression de l'altitude
), donner l'expression de l'altitude 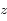 en fonction de la coordonnée
en fonction de la coordonnée 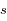 .
.
Question 3)
Reprendre les questions 1) et 2) pour donner l'expression de 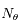 , la densité de colonne pour une position
, la densité de colonne pour une position 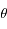 quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc
quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc 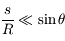 .
.
Dans ce cas, on utilise le théorème de Pythagore généralisé (ou loi des cosinus)
Auteur: Stéphane Erard
 Calcul de la masse d'air
Calcul de la masse d'air
Difficulté : ☆
Temps : 30 min
Le rapport  de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation
de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation 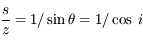 , où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
, où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
On veut maintenant calculer exactement la longueur du chemin optique parcouru par les rayons lumineux dans l'atmosphère pour étudier la validité de l'approximation précédente.
Question 1)
Reprendre la question 3 de l'exercice précédent : dériver une relation entre l'altitude 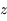 et la coordonnée
et la coordonnée 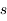 pour une hauteur
pour une hauteur 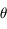 quelconque.
quelconque.
On exprimera cette relation en fonction de l'angle zénital  (compté à partir de la verticale locale).
(compté à partir de la verticale locale).
Question 2)
Résoudre en 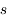 .
.
Question 3)
Tracer 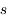 en fonction de l'angle zénital
en fonction de l'angle zénital  et comparer avec l'approximation usuelle en sécante (
et comparer avec l'approximation usuelle en sécante (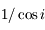 ).
).
Question 4)
Quel est le domaine de validité de l'approximation en sécante ?
Quels autres phénomènes affectent la diffusion dans ces conditions ? Conclusion ?
Auteur: Stéphane Erard
Depuis l'antiquité jusqu'au XVIIe siècle, plusieurs conceptions de la lumière se sont succédées. Il était notamment impossible de dire si la lumière se propage instantanément ou à vitesse finie. En 1676, Ole Römer met en évidence une vitesse de propagation finie, dont il estime un ordre de grandeur correct à partir de l'observation des satellites de Jupiter. Cette méthode est reproduite ici.
Auteur: Stéphane Erard
 Mouvement des satellites de Jupiter
Mouvement des satellites de Jupiter
Difficulté : ☆
Temps : 60 min
En 1668, Gian Domenico Cassini a publié les premières éphémérides des satellites galiléens. L'intérêt de ces phénomènes était de fournir une horloge visible et consultable partout sur Terre : les débuts d'éclipse des satellites. Ceux-ci permettent de déterminer la longitude du lieu d'observation par comparaison avec une horloge locale.
Dans les années suivantes, Römer mit néanmoins en évidence des écarts importants avec ses propres observations de Io, le plus proche satellite de Jupiter, et le plus rapide. Ces écarts augmentaient (jusqu'à 11 minutes) puis diminuaient avec une périodicité d'un an.
Question 1)
On considère la situation de la Figure 1, lorsque Io est en émersion au point D (il sort de l'ombre de Jupiter). Durant un premier événement la Terre est au point L de son orbite, lors du suivant elle est en K.
Si la lumière se propage instantanément, quel intervalle sépare les deux événements ?
Question 2)
Même question en supposant que la lumière se déplace à la vitesse c. Remarques sur la Figure 1 ? Préciser les approximations implicites qu'on a fait.
Question 3)
Calculer en unités astronomiques la distance Terre-Jupiter à l'opposition (lorsque les deux planètes sont au plus près).
Question 4)
On effectue une première observation d'éclipse à l'opposition. A quel moment peut-on effectuer une seconde observation pour laquelle le décalage sera maximum ?
Question 5)
On observe 261 jours après l'opposition. De quels angles se sont déplacés Jupiter et la Terre sur leurs orbites depuis l'opposition ? Quel est l'angle Jupiter-Soleil-Terre à ce moment ?
On donne la période sidérale de Jupiter, 4335,35 jours, bien connue à l'époque.
Question 6)
Calculer la distance Terre-Jupiter  en unités astronomiques au moment de la deuxième observation.
en unités astronomiques au moment de la deuxième observation.
La distance Soleil-Jupiter est de 5,2 unités astronomiques.
Question 7)
Le second événement est observé avec 13,5 min de retard par rapport à un phénomène régulier. En déduire une estimation de la vitesse de la lumière.
-
Question 1
Solution :
On a comme précédemment :
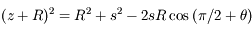
Soit
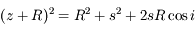
-
Question 2
Solution :
On a une équation de second degré :
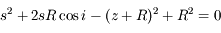
dont le discriminant est :
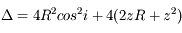
et les solutions :
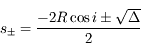
Seule la solution positive représente une distance :
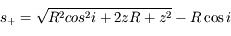
-
Question 3
Solution :
Masse d'air
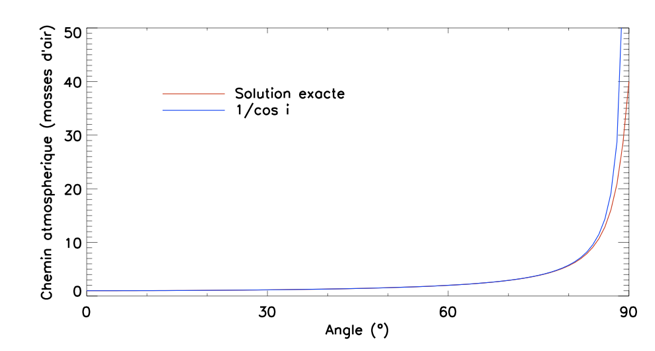
L'approximation en sécante diverge près de l'horizon, où elle ne représente plus une solution physique.
Pour convertir les masses d'air en densité de colonne, il faut fixer une valeur pour la masse d'air 1. On prend naturellement l'échelle de hauteur fournie par la loi barométrique, ou dérivée d'une mesure de pression locale.
-
Question 4
Solution :
On voit que l'approximation par la sécante est très bonne jusqu'à des distances zénitales au-delà de 80° — les télescopes professionnels refusent de pointer si bas sur l'horizon.
Avec l'augmentation de la masse d'air, les rayons lumineux sont non seulement atténués, mais également déviés - on peut voir dans certaines conditions des objets situés sous l'horizon géométrique. L'intérêt de l'expression dérivée ci-dessus est donc limité, la correction optique de réfraction étant en pratique plus importante.
-
Question 1
Solution :
Si la lumière se propage instantanément les événements sont observés à intervalles réguliers, qui ne dépendent que du mouvement de Io. Cet intervalle est simplement la période de révolution de Io autour de Jupiter (T ~ 42h 28 min).
-
Question 2
Solution :
Si la lumière se propage à vitesse finie, le premier événement est observé avec un décalage 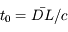 , le second avec
, le second avec 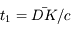 . L'intervalle entre les observations est donc
. L'intervalle entre les observations est donc 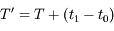 . Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et
. Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et 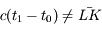 .
.
On a considéré implicitement que tous les mouvements de révolution s'effectuent dans le même plan, ce qui n'est pas tout à fait vrai. Cette hypothèse conditionnera la précision du résultat sur l'estimation de c.
-
Question 3
Solution :
On appelle 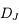 la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors
la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors 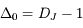 ua.
ua.
-
Question 4
Solution :
Lors de la conjonction (lorsque les deux planètes sont éloignées au maximum) l'observation est impossible : le Soleil s'interpose devant Jupiter. La seconde observation s'effectue donc soit avant soit après la conjonction, lorsque l'écart angulaire entre Jupiter et le Soleil est suffisamment grand pour observer de nouveau les satellites (typiquement ~ 20°).
-
Question 5
Aide :
On donne la période sidérale de Jupiter, 4335,35 jours, bien connue à l'époque.
Solution :
En 261 jours, la Terre s'est déplacée d'un angle 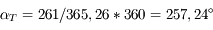
Jupiter s'est déplacée de 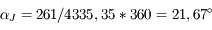
L'angle Jupiter-Soleil-Terre est donc à ce moment 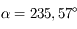
-
Question 6
Aide :
La distance Soleil-Jupiter est de 5,2 unités astronomiques.
Solution :
On considère le triangle JST. La loi des cosinus (ou théorème d'Al-Kashi) donne :
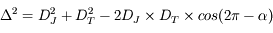
Soit 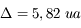
-
Question 7
Solution :
La différence de trajet est 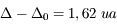
On a donc 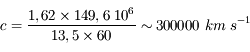
L'unité astronomique (distance Terre-Soleil) et la distance Jupiter-Soleil étaient les plus gros facteurs d'incertitude à l'époque. Römer semble avoir trouvé une valeur de 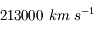 (soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
(soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
Cette étude peut être considérée comme le premier exemple historique d'effet Doppler-Fizeau, c'est-à-dire la variation de période apparente d'un phénomène régulier avec le déplacement de l'observateur.
 Zone visible d'une montagne ou d'un satellite
Zone visible d'une montagne ou d'un satellite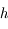 , sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
, sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
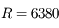 km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
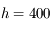 km?
km?
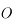 (centre de la Terre),
(centre de la Terre), 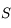 (satellite) et
(satellite) et 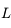 (un lieu de la Terre où
(un lieu de la Terre où 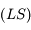 est tangent à
la Terre. On note
est tangent à
la Terre. On note 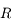 le rayon de la Terre.
le rayon de la Terre.
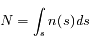
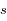 est la coordonnée le long du trajet du rayon et
est la coordonnée le long du trajet du rayon et 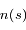 est la densité atmosphérique au point de coordonnée
est la densité atmosphérique au point de coordonnée 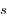 .
.
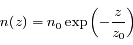
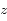 est l'altitude (mesurée verticalement),
est l'altitude (mesurée verticalement), 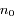 est la densité au niveau du sol, et
est la densité au niveau du sol, et 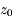 est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la
est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la 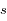 sur le trajet du rayon de Soleil, et d'altitude
sur le trajet du rayon de Soleil, et d'altitude 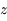 .
. 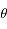 est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.

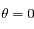 ), donner l'expression de l'altitude
), donner l'expression de l'altitude 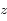 en fonction de la coordonnée
en fonction de la coordonnée 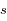 .
.
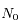 , la densité de colonne au Soleil couchant (
, la densité de colonne au Soleil couchant (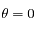 ). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour
). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour 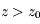 ; on peut donc tronquer l'intégrale à une altitude maximum telle que
; on peut donc tronquer l'intégrale à une altitude maximum telle que 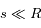 (l'atmosphère est fine par rapport à la taille de la planète).
(l'atmosphère est fine par rapport à la taille de la planète).
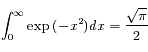
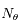 , la densité de colonne pour une position
, la densité de colonne pour une position 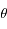 quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc
quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc 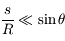 .
.
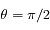 . Calculer le rapport
. Calculer le rapport 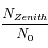 . Pour l'application numérique on prendra
. Pour l'application numérique on prendra 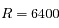 km,
km, 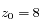 km (échelle de hauteur de l'atmosphère terrestre).
km (échelle de hauteur de l'atmosphère terrestre).
 de l'exercice précédent est appelé
de l'exercice précédent est appelé 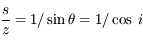 , où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'
, où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'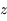 et la coordonnée
et la coordonnée 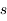 pour une hauteur
pour une hauteur 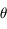 quelconque.
quelconque.
 (compté à partir de la verticale locale).
(compté à partir de la verticale locale).
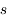 .
.
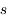 en fonction de l'angle zénital
en fonction de l'angle zénital  et comparer avec l'approximation usuelle en sécante (
et comparer avec l'approximation usuelle en sécante (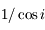 ).
).

 en unités astronomiques au moment de la deuxième observation.
en unités astronomiques au moment de la deuxième observation.
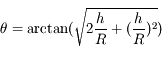 . On peut écrire aussi
. On peut écrire aussi
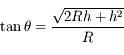
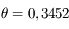 radians. La distance maximale est
radians. La distance maximale est 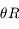 , soit
, soit 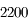 km.
km.
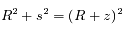
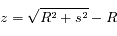
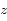 au premier ordre :
au premier ordre :
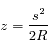
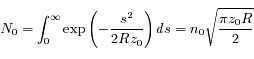
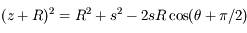
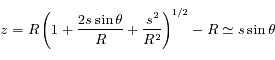
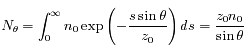
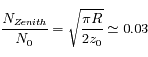
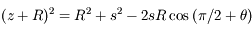
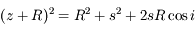
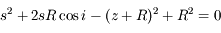
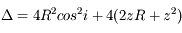
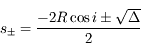
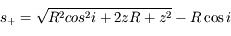

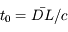 , le second avec
, le second avec 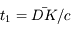 . L'intervalle entre les observations est donc
. L'intervalle entre les observations est donc 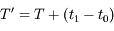 . Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et
. Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et 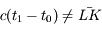 .
.
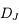 la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors
la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors 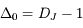 ua.
ua.
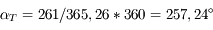
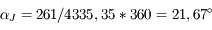
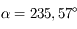
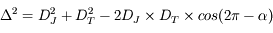
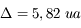
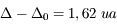
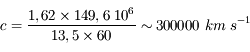
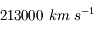 (soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
(soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.