 |  |  |  |  |  |
Calotte sphérique |
Auteur : Marc Fouchard
Etant donné qu'un observateur sur Terre se trouve à une distance finie de la Lune, lorsqu'il regarde la Lune il ne perçoit qu'une calotte et non un hemisphère. L'objectif de cet exercice est de trouver la surface de la partie de la Lune observable depuis la Terre et de comparer cette surface à celle de l'hémisphère.
On note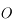 
l'observateur, 
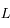le centre de la Lune et 
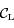l'intersection de la sphère correspondant à la Lune avec un plan contenant la droite 
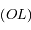. Ainsi 
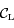est un cercle de centre 
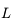et de rayon 
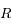, où 
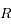est le rayon de la Lune. On note 
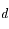la distance 
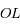. Les tangentes à 
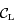passant par 
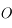coupent 
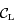en 
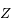et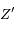 
. Soit 
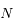le point de 
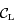tel que 
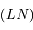est perpendiculaire à 
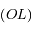avec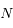 
du même coté que 
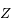de la droite 
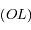. On note 
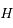le projeté orthogonal de 
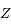sur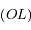 
, 
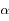l'angle 
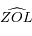et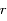 
la distance 
.
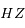La calotte visible depuis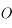 
correspond donc à la partie de la surface de la Lune tournée vers 
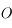et de frontière le cercle de centre 
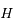et de rayon 
.
 |  |
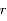