Ex: Redshift

Auteurs: Jérôme Thiébaut, Marc Fouchard, Alain Vienne

Auteur: Jérôme Thiébaut

Redshift

Difficulté : ☆☆ Temps : 20mn

On considère un photon radial émis à une distance 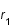r_1 au temps 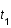t_1 par une galaxie lointaine. Ce photon nous est reçu au temps 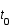t_0 en r=0 .

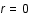Sa trajectoire est décrite par la métrique: 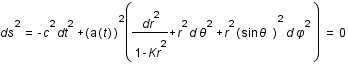ds^2=-c^2*dt^2+a(t)^2*(dr^2/(1-Kr^2)+r^2*d*theta^2+r^2*sin(theta)^2*d*phi^2)=0 .

Question 1)

Simplifier la métrique compte tenu de la nature du photon et exprimer l'égalité sous forme intégrale.

Aide Solution

Question 2)

Un deuxième photon est émis à 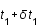t_1 + delta*t_1 et est reçu en 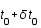t_0 + delta*t_0 . Quelle est la nouvelle égalité sous forme intégrale ?

Solution

Question 3)

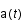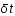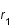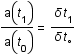Sachant que a(t) est considéré comme constant pendant un temps delta*t faible et que la distance comobile ( r_1 ) est constante par définition, montrer que a(t_1)/a(t_0)=delta*t_1/(delta*t_°) .

Aide Solution

Question 4)

Le redshift 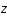est défini comme suit: 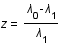z=(lambda_0 -lambda_1)/lambda_1 , où 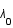est la longueur d'onde du photon reçu et 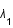celle du photon émis.

Sachant qu'à un 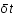delta*t correspond une longueur d'onde 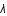lambda , et que par convention, 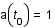a(t_0)=1 , relier la quantité 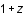1+z au facteur d'échelle.

Solution