 |  |  |  |  |  |
Redshift |
Auteur : Jérôme Thiébaut
En coordonnées cartésiennes, un élément de longueur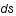 
se calcule selon le théorème de Pythagore:
.
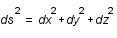Ceci donne en coordonnées sphériques:
.
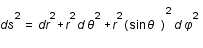On voit que l'expression de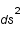 
dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
,
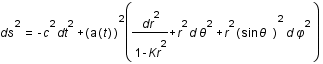ou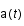 
est le facteur d'échelle qui décrit l'expansion de l'univers, 
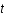le temps, 
, 
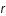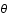et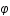 
les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) , 
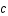la vitesse de la lumière et 
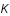la courbure de l'univers.
Pour un photon, la trajectoire est telle que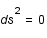 
.
On se propose dans cet exercice d'étudier la trajectoire d'un photon radial afin de relier le redshift (ou décallage spectral),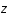 
, au facteur d'échelle, 
.
 |  |
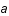