 |  |  |  |  |  |
Ex : Calotte sphérique |
Calotte sphériqueDifficulté : ☆ Temps : 30 mn
Faire la figure qui correspond à l'énoncé.
Soit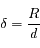 
, calculer 
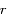en fonction de 
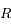et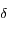 
.
Calculer la surface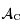 
de la calotte visible depuis 
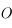en fonction de la surface d'un hémisphère de la Lune 
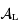et de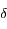 
.
Montrer que dans le cas d'un astronaute autour de la Terre la portion de surface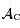 
de la Terre visible par l'astronaute s'écrit sous la forme de la surface d'un cercle dont on déterminera le rayon en fonction du rayon de la Terre 
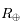et de l'altitude 
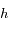de l'astronaute. On supposera donc que 
.
 |  |
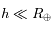. On en déduit que:
.
rectangle en 
on a:
.
On en déduit que:
.
,
où 
est l'angle 
et 
l'angle 
avec 
un point de la calotte, 
son projeté orthogonal sur la droite 
et 
le point de la droite 
dont la projection orthogonale sur 
est 
.
.
C'est-à-dire:
.
, ainsi 
Ainsi 
.