

Ex: Potentiel gravitationnel de la Terre |
Difficulté : ☆ Temps : 1h
Soit un anneau de centre 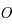 et de rayon
et de rayon 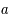 . On repère un point
. On repère un point 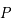 de coordonnées sphériques
de coordonnées sphériques 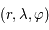 (dont le plan horizontal est le plan de l'anneau).
(dont le plan horizontal est le plan de l'anneau).
Soit 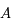 un point de l'anneau. Il fait un angle
un point de l'anneau. Il fait un angle 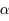 avec le premier axe (même origine que l'angle
avec le premier axe (même origine que l'angle 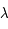 ).
).
Calculer la distance 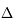 de
de 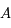 à
à 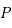 .
.
Calculer 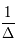 en se limitant aux termes de degré 2 au plus en
en se limitant aux termes de degré 2 au plus en 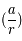 .
.
Pour avoir le potentiel total de l'anneau, il faut sommer cette expression pour 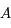 variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à
variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à 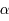 qui varie de
qui varie de 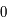 à
à 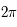 .
.
A partir de l'expression précédente, calculer 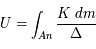 .
.
En comparant cette expression avec celle utilisant le coefficient 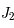 , donner le rayon de l'anneau correspondant au potentiel terrestre. On donne
, donner le rayon de l'anneau correspondant au potentiel terrestre. On donne 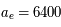 km.
km.