Invariants adiabatiques dans le champ dipolaire d'une planète
Dans le cas des particules dans un champ magnétique
dipolaire, les premier mouvement quasi périodique
est le mouvement de rotation à la fréquence
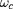
. L'invariant adiabatique associé à ce mouvement
périodique est le moment magnétique

. Au lieu de particule, on décrit alors la trajectoire
du centre guide associé à la particule. Le centre
guide est défini par sa vitesse parallèle, sa position
(un vecteur de dimension 3), et son moment
magnétique (dont la valeur est fixée une fois
pour toute pour chaque centre guide).
On voit alors que le centre guide, si il correspond
à une particule piégée, a un mouvement de
rebond, lui aussi périodique, de période
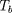
très supérieure à la giropériode
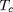
. On associe à ce mouvement oscillatoire un
invariant adiabatique :
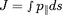
. L'intégrale est calculée sur un mouvement
aller et retour (période
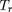
). On l'appelle le second invariant adiabatique,
ou l' invariant longitudinal. Au lieu de définir
un centre guide, on peut alors définir un arc de
ligne de champ qui correspond à la trajectoire
du centre guide entre deux points rebonds. Cet
arc est défini par sa position azimutale
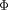
, son rayon vecteur
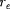
à l'equateur, et quelque chose qui caractérise
la latitude des points miroir, par exemple
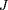
. On se rend compte que la dérive azimutale de
cette sorte de "méta-particule", la même que
la dérive azimutale du centre guide, permet de
définir un troisième invariant adiabatique, ou
invariant de flux magnétique
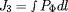
avec
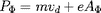
. Cette intégrale est calculée sur un tour complet
(période
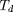
). On peut même montrer qu'une forme approchée
de cet invariant est

où
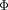
est le flux de champ magnétique à travers
la portion de plan équatorial délimitée par la
trajectoire de la particule (c'est la surface en
gris sur la figure ??).

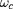 . L'invariant adiabatique associé à ce mouvement
périodique est le moment magnétique
. L'invariant adiabatique associé à ce mouvement
périodique est le moment magnétique
 . Au lieu de particule, on décrit alors la trajectoire
du centre guide associé à la particule. Le centre
guide est défini par sa vitesse parallèle, sa position
(un vecteur de dimension 3), et son moment
magnétique (dont la valeur est fixée une fois
pour toute pour chaque centre guide).
. Au lieu de particule, on décrit alors la trajectoire
du centre guide associé à la particule. Le centre
guide est défini par sa vitesse parallèle, sa position
(un vecteur de dimension 3), et son moment
magnétique (dont la valeur est fixée une fois
pour toute pour chaque centre guide).
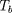 très supérieure à la giropériode
très supérieure à la giropériode
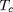 . On associe à ce mouvement oscillatoire un
invariant adiabatique :
. On associe à ce mouvement oscillatoire un
invariant adiabatique :
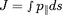 . L'intégrale est calculée sur un mouvement
aller et retour (période
. L'intégrale est calculée sur un mouvement
aller et retour (période
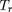 ). On l'appelle le second invariant adiabatique,
ou l' invariant longitudinal. Au lieu de définir
un centre guide, on peut alors définir un arc de
ligne de champ qui correspond à la trajectoire
du centre guide entre deux points rebonds. Cet
arc est défini par sa position azimutale
). On l'appelle le second invariant adiabatique,
ou l' invariant longitudinal. Au lieu de définir
un centre guide, on peut alors définir un arc de
ligne de champ qui correspond à la trajectoire
du centre guide entre deux points rebonds. Cet
arc est défini par sa position azimutale
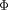 , son rayon vecteur
, son rayon vecteur
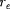 à l'equateur, et quelque chose qui caractérise
la latitude des points miroir, par exemple
à l'equateur, et quelque chose qui caractérise
la latitude des points miroir, par exemple
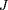 . On se rend compte que la dérive azimutale de
cette sorte de "méta-particule", la même que
la dérive azimutale du centre guide, permet de
définir un troisième invariant adiabatique, ou
invariant de flux magnétique
. On se rend compte que la dérive azimutale de
cette sorte de "méta-particule", la même que
la dérive azimutale du centre guide, permet de
définir un troisième invariant adiabatique, ou
invariant de flux magnétique
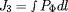 avec
avec
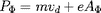 . Cette intégrale est calculée sur un tour complet
(période
. Cette intégrale est calculée sur un tour complet
(période
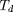 ). On peut même montrer qu'une forme approchée
de cet invariant est
). On peut même montrer qu'une forme approchée
de cet invariant est
 où
où
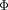 est le flux de champ magnétique à travers
la portion de plan équatorial délimitée par la
trajectoire de la particule (c'est la surface en
gris sur la figure ??).
est le flux de champ magnétique à travers
la portion de plan équatorial délimitée par la
trajectoire de la particule (c'est la surface en
gris sur la figure ??).