Invariants adiabatiques
On a vu qu'au premier ordre, le moment
magnétique est conservé et on l'a démontré
dans le cas simplifié ou la variation temporelle
des champs électromagnétiques est nulle. Il
existe deux autres invariants adiabatiques
associés au mouvement des centres guide
autour de la Terre. L'un est associé au
mouvement de rebond des centre guides entre
deux points miroir. L'autre est associé à la
dérive azimutale des particules.
Soit un système hamiltonien (par exemple une
particule chargée dans un champ électromagnétique)
défini par une énergie
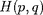
fonction des variables canoniques

et

. On suppose que ce système possède des trajectoires
périodiques lorsque
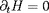
. Si
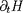
est faible (système variant lentement en fonction
du temps), alors on peut définir des trajectoires
presque périodiques pour lesquelle
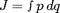
estconservé. Moins imprécisément, les variations
de
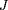
sont au plus de l'ordre de
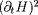
, c'est à dire qu'on peut les négliger si le système
varie lentement. On appelle
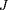
un invariant adiabatique.

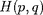 fonction des variables canoniques
fonction des variables canoniques
 et
et
 . On suppose que ce système possède des trajectoires
périodiques lorsque
. On suppose que ce système possède des trajectoires
périodiques lorsque
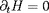 . Si
. Si
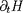 est faible (système variant lentement en fonction
du temps), alors on peut définir des trajectoires
presque périodiques pour lesquelle
est faible (système variant lentement en fonction
du temps), alors on peut définir des trajectoires
presque périodiques pour lesquelle
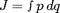 estconservé. Moins imprécisément, les variations
de
estconservé. Moins imprécisément, les variations
de
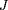 sont au plus de l'ordre de
sont au plus de l'ordre de
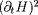 , c'est à dire qu'on peut les négliger si le système
varie lentement. On appelle
, c'est à dire qu'on peut les négliger si le système
varie lentement. On appelle
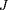 un invariant adiabatique.
un invariant adiabatique.