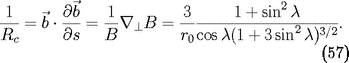Le champ magnétique diplolaire
Le champ magnétique dipolaire est un champ
dont le rotationel est nul, sauf en l'origine qui
est un point singulier. Puisque le rotationel
est nul, il n'y a pas de courant électrique
associé à ce champ magnétique (sauf au
point singulier). C'est donc un champ qui
peut exister dans le vide. C'est loin d'être le
seul, mais il est simple, et il sert fréquement
à modéliser l'environnement magnétique des
astres : planètes, Soleil calme, puslars.
Un champ magnétique dipôlaire dérive d'un
potentiel vecteur
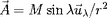
, défini ici à partir de coordonnées sphériques et de
la latitude
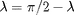
. On peut aussi l'exprimer comme le gradient d'un
potentiel scalaire
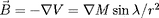
. Les composantes (toujours en coordonnées
sphériques) sont
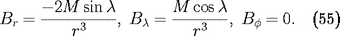
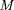
est l'intensité du dipôle, il vaut pour la
Terre
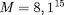
T.m

. Un champ magnétique dipolaire vérifie
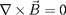
. L'équation d'un ligne de champ est
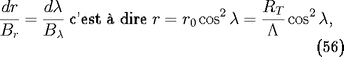
où
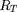
est le rayon de la Terre,
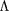
est la latitude du point où la ligne de champ
croise la surface de la Terre Le rayon de
courbure
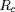
d'une ligne de champ est donné par
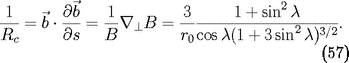

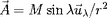 , défini ici à partir de coordonnées sphériques et de
la latitude
, défini ici à partir de coordonnées sphériques et de
la latitude
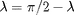 . On peut aussi l'exprimer comme le gradient d'un
potentiel scalaire
. On peut aussi l'exprimer comme le gradient d'un
potentiel scalaire
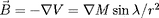 . Les composantes (toujours en coordonnées
sphériques) sont
. Les composantes (toujours en coordonnées
sphériques) sont 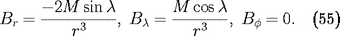
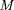 est l'intensité du dipôle, il vaut pour la
Terre
est l'intensité du dipôle, il vaut pour la
Terre
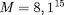 T.m
T.m
 . Un champ magnétique dipolaire vérifie
. Un champ magnétique dipolaire vérifie
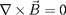 . L'équation d'un ligne de champ est
. L'équation d'un ligne de champ est 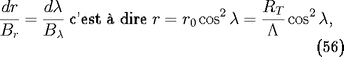
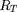 est le rayon de la Terre,
est le rayon de la Terre,
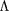 est la latitude du point où la ligne de champ
croise la surface de la Terre Le rayon de
courbure
est la latitude du point où la ligne de champ
croise la surface de la Terre Le rayon de
courbure
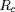 d'une ligne de champ est donné par
d'une ligne de champ est donné par