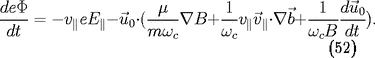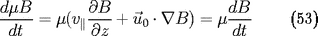Une démonstration de la conservation du moment magnétique
Voici la démonstration dans le cas où les champs
électrique et magnétique sont statiques.
Dans ce cas l'énergie totale (cinétique plus
potentielle) de la particule est conservée :
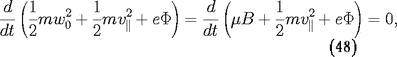
où
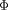
est le potentiel électrostatique (
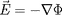
). La seconde égalité vient de la définition
18
du moment magnétique. La variation de
l'énergie cinétique parallèle se déduit de
17
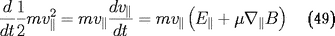
La variation d'énergie potentielle électrostatique
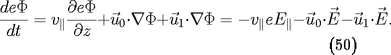
Le terme
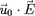
est nul (voir la définition
31 de
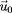
). Le terme suivant se développe en utilisant
19 :
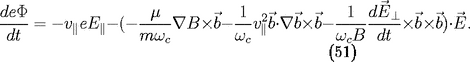
Grace à la définition de
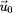
,
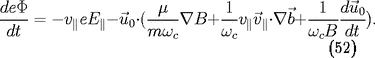
En réunissant
48,
49, et
52, il reste
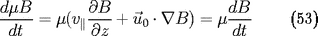
d'ou il résulte


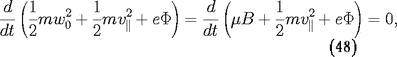
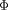 est le potentiel électrostatique (
est le potentiel électrostatique (
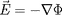 ). La seconde égalité vient de la définition 18
du moment magnétique. La variation de
l'énergie cinétique parallèle se déduit de 17
). La seconde égalité vient de la définition 18
du moment magnétique. La variation de
l'énergie cinétique parallèle se déduit de 17
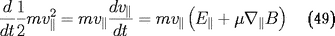
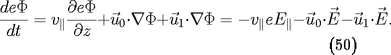
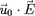 est nul (voir la définition 31 de
est nul (voir la définition 31 de
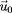 ). Le terme suivant se développe en utilisant 19 :
). Le terme suivant se développe en utilisant 19 :
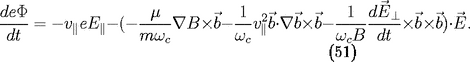
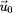 ,
,