Récapitulation sur le mouvement du centre guide
Le mouvement du centre guide est régi par une
équation qui décrit la composante parallèle de son
accélération et par une équation qui donne
explicitement les composantes perpendiculaires de
sa vitesse. L'équation sur l'accélération parallèle
(
47) ne comprend que des termes d'ordre 1 :
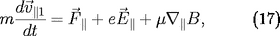
où

est le moment magnétique de la particule qui est le
rapport entre l'énergie cinétique associée à sa
rotation d'ordre 0 et l'amplitude du champ
magnétique
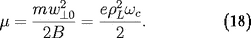
La vitesse perpendiculaire contient un terme
d'ordre 0 et des termes d'ordre 1:
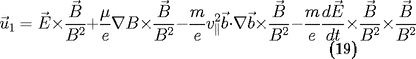
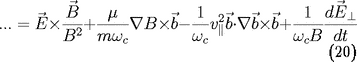
La seconde expression de la vitesse de dérive fait
intervenir la définition de

, le développement du double produit vectoriel
(pour le terme dù à la variation de
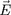
), et a l'usage, autant que possible de la
girofréquence
5. On obtient quatre termes
de dérive qui s'appellent respectivement
la dérive de champs croisés, la dérive de
gradient, la dérive de courbure et la dérive de
polarisation.

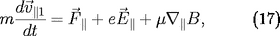
 est le moment magnétique de la particule qui est le
rapport entre l'énergie cinétique associée à sa
rotation d'ordre 0 et l'amplitude du champ
magnétique
est le moment magnétique de la particule qui est le
rapport entre l'énergie cinétique associée à sa
rotation d'ordre 0 et l'amplitude du champ
magnétique 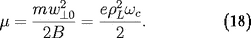
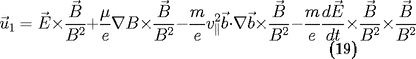
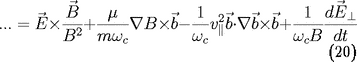
 , le développement du double produit vectoriel
(pour le terme dù à la variation de
, le développement du double produit vectoriel
(pour le terme dù à la variation de
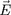 ), et a l'usage, autant que possible de la
girofréquence 5. On obtient quatre termes
de dérive qui s'appellent respectivement
la dérive de champs croisés, la dérive de
gradient, la dérive de courbure et la dérive de
polarisation.
), et a l'usage, autant que possible de la
girofréquence 5. On obtient quatre termes
de dérive qui s'appellent respectivement
la dérive de champs croisés, la dérive de
gradient, la dérive de courbure et la dérive de
polarisation.