Vitesses de dérive déduites des forces moyennes
Tout comme on l'a fait pour l'approximation
d'ordre zéro, on peut déduire de chaque
force
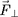
appliquée perpendiculairement au champ
magnétique une vitesse de dérive
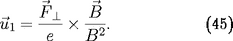
Voici la solution génerale, dans laquelle
on reconnaitra les trois forces que nous
avons calculé dans des cas particuliers.
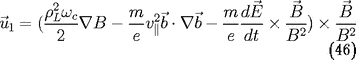
L'équation sur le mouvement parallèle au champ
magnétique, est
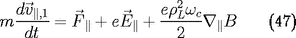
On en déduit que l'effet d'un gradient de champ
magnétique, d'une variation temporelle du
champ électrique et d'une courbure des
lignes de champ est d'introduire une dérive
perpendiculaire du mouvement des centres guides,
dont la vitesse est donnée par la relation
46. Pour des échelles de temps grandes
devant
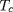
la vitesse est
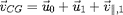
, et on peut définir le vecteur
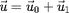
qui est la composante de
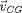
perpendiculaire à
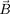
. La vitesse parallèle
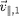
, est donnée par la relation
47.
On appelera centre guide le bidule associé à une
particule chargée qui se déplace avec la
vitesse
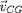
. On peut dire que le centre guide est le centre
autour duquel tourne la particule avec la
vitesse
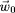
, la vitesse totale de la particule a donc une
composante de haute fréquence
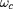
donnée par
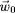
et une composante plus faible variant lentement
donnée par
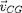
:
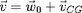
.

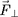 appliquée perpendiculairement au champ
magnétique une vitesse de dérive
appliquée perpendiculairement au champ
magnétique une vitesse de dérive 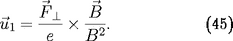
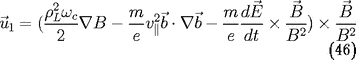
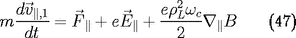
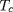 la vitesse est
la vitesse est
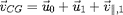 , et on peut définir le vecteur
, et on peut définir le vecteur
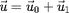 qui est la composante de
qui est la composante de
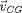 perpendiculaire à
perpendiculaire à
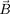 . La vitesse parallèle
. La vitesse parallèle
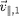 , est donnée par la relation 47.
On appelera centre guide le bidule associé à une
particule chargée qui se déplace avec la
vitesse
, est donnée par la relation 47.
On appelera centre guide le bidule associé à une
particule chargée qui se déplace avec la
vitesse
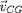 . On peut dire que le centre guide est le centre
autour duquel tourne la particule avec la
vitesse
. On peut dire que le centre guide est le centre
autour duquel tourne la particule avec la
vitesse
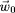 , la vitesse totale de la particule a donc une
composante de haute fréquence
, la vitesse totale de la particule a donc une
composante de haute fréquence
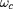 donnée par
donnée par
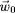 et une composante plus faible variant lentement
donnée par
et une composante plus faible variant lentement
donnée par
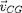 :
:
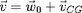 .
.