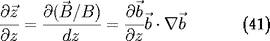Forces dues à la rotation du repère
Il ne suffit pas de dériver les coordonnées pour avoir
la dérivée de la vitesse. En effet, on a vu que le
repère est construit de manière à ce que le
vecteur
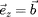
soit parallèle à la direction locale des lignes de
champ. Lorsque la particule avance, ce référentiel
bouge et il faut tenir compte de la variation
des vecteurs qui définissent ce réferentiel.
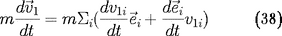
La force d'inertie du à la rotation du repère, ou
encore la force centripète due à la courbure de la
trajectoire de la particule est

Comme
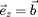
, la différentielle d'abscisse curviligne
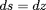
. Donc,
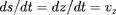
. En développant la dérivée totale
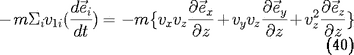
Ici on a supposé pour se simplifier la vie que les
variations temporelles du champ magnétique sont
négligeables devant ses dérivées spatiales. On ne
fait pas ici d'hypothèse particulière sur les dérivées
spatiales. Les dérivées sont constantes, le
produit
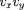
varie comme
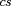
qui est de moyenne nulle. La valeur moyenne
de
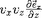
est nulle. De même, la valeur moyenne
de
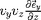
est nulle. Un petit calcul simple montre
que
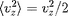
(moyenne d'un cosinus carré). D'autre part
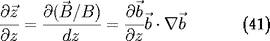
la force s'écrit donc de manière "canonique"


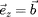 soit parallèle à la direction locale des lignes de
champ. Lorsque la particule avance, ce référentiel
bouge et il faut tenir compte de la variation
des vecteurs qui définissent ce réferentiel.
soit parallèle à la direction locale des lignes de
champ. Lorsque la particule avance, ce référentiel
bouge et il faut tenir compte de la variation
des vecteurs qui définissent ce réferentiel.
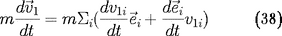

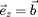 , la différentielle d'abscisse curviligne
, la différentielle d'abscisse curviligne
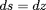 . Donc,
. Donc,
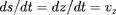 . En développant la dérivée totale
. En développant la dérivée totale 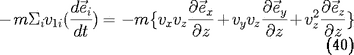
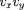 varie comme
varie comme
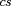 qui est de moyenne nulle. La valeur moyenne
de
qui est de moyenne nulle. La valeur moyenne
de
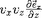 est nulle. De même, la valeur moyenne
de
est nulle. De même, la valeur moyenne
de
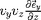 est nulle. Un petit calcul simple montre
que
est nulle. Un petit calcul simple montre
que
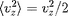 (moyenne d'un cosinus carré). D'autre part
(moyenne d'un cosinus carré). D'autre part