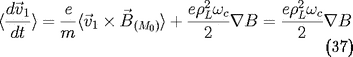Forces dues au gradient de B
: On va se placer dans une géométrie un peu
simplifiée. On supposera que le champ magnétique
conserve son orientation
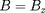
et qu'il ne varie que suivant la direction

; la matrice du gradient de
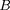
n'a donc que la dérivée
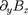
.
L'équation du mouvement s'écrit
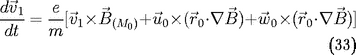
On s'intéresse aux deux derniers termes qui
viennent du gradient de champ magnétique.
Comme
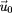
est un terme constant (on prendra en compte
ses variations lors de l'étude des termes
d'inertie) on vérifie que tous les produits qui
apparaissent dans le second terme ont une
moyenne nulle. Dans le troisième terme,
il y a des facteurs non nuls en moyenne,
et on va en détailler un peu le calcul. En
explicitant
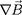
et la solution à l'ordre zéro,
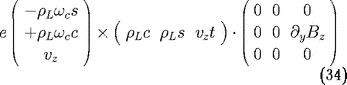
En développant,
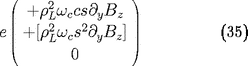
Seuls le terme de
35 marqué entre crochets a une
moyenne non nulle. En valeur moyenne, il reste
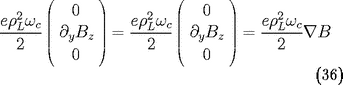
la dernière expression vient de ce que
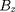
est égal à la norme
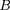
de
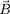
. L'équation du mouvement moyen s'écrit
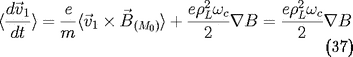
Bien qu'on l'aie calculé dans un cas très
particulier, cette expression demeure vraie dans le
cas d'un gradient quelconque de champ
magnétique. Le calcul dans le cas général n'est pas
beaucoup plus compliqué, il est seulement plus
long.

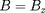 et qu'il ne varie que suivant la direction
et qu'il ne varie que suivant la direction
 ; la matrice du gradient de
; la matrice du gradient de
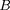 n'a donc que la dérivée
n'a donc que la dérivée
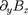 .
L'équation du mouvement s'écrit
.
L'équation du mouvement s'écrit 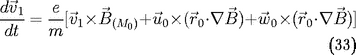
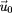 est un terme constant (on prendra en compte
ses variations lors de l'étude des termes
d'inertie) on vérifie que tous les produits qui
apparaissent dans le second terme ont une
moyenne nulle. Dans le troisième terme,
il y a des facteurs non nuls en moyenne,
et on va en détailler un peu le calcul. En
explicitant
est un terme constant (on prendra en compte
ses variations lors de l'étude des termes
d'inertie) on vérifie que tous les produits qui
apparaissent dans le second terme ont une
moyenne nulle. Dans le troisième terme,
il y a des facteurs non nuls en moyenne,
et on va en détailler un peu le calcul. En
explicitant
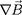 et la solution à l'ordre zéro,
et la solution à l'ordre zéro, 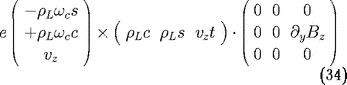
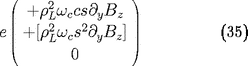
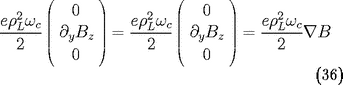
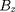 est égal à la norme
est égal à la norme
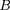 de
de
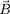 . L'équation du mouvement moyen s'écrit
. L'équation du mouvement moyen s'écrit